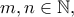 τότε να αποδείξετε ότι:
τότε να αποδείξετε ότι: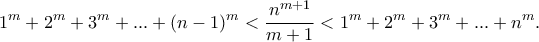
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
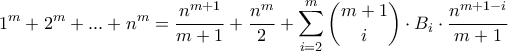
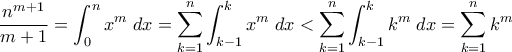
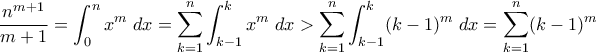
Γιώργο, να μας δώσεις λίγες περισσότερες λεπτομέρειες; Προς το παρόν δεν βλέπω πως μπορεί να χρησιμοποιηθεί.G.Bas έγραψε:Πιστεύω πως λύνεται και με τη formula του Bernulli, η οποία λέει
Επειδή βλέπω ότι δεν υπάρχει στοιχειώδης απόδειξη γράφω μια που γνωρίζω από τα μαθητικά μου χρόνια.
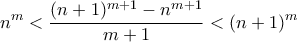 (1)
(1)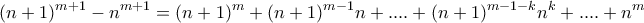
 .
.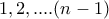 παίρνουμε
παίρνουμε 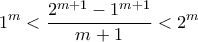
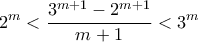
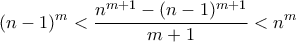
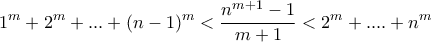
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες