![\overrightarrow{\alpha}:[0,L]\subset{\mathbb{R}}\longrightarrow{\mathbb{R}}^2\,;\; s\longmapsto\overrightarrow{\alpha}(s) \overrightarrow{\alpha}:[0,L]\subset{\mathbb{R}}\longrightarrow{\mathbb{R}}^2\,;\; s\longmapsto\overrightarrow{\alpha}(s)](/forum/ext/geomar/texintegr/latexrender/pictures/871c14e7c6d6eac4af3d560d94f79bfa.png) μια κλειστή, κυρτή, θετικά προσανατολισμένη, λεία παραμετρική καμπύλη με την
μια κλειστή, κυρτή, θετικά προσανατολισμένη, λεία παραμετρική καμπύλη με την  να είναι παράμετρος μήκους τόξου. Θεωρούμε την "παράλληλη" καμπύλη
να είναι παράμετρος μήκους τόξου. Θεωρούμε την "παράλληλη" καμπύλη ![\overrightarrow{\gamma}:[0,L]\subset{\mathbb{R}}\longrightarrow{\mathbb{R}}^2 \overrightarrow{\gamma}:[0,L]\subset{\mathbb{R}}\longrightarrow{\mathbb{R}}^2](/forum/ext/geomar/texintegr/latexrender/pictures/e8134b59b4281b1dbb337b2548438c27.png) με τύπο
με τύπο 
όπου
 θετικός σταθερός αριθμός και
θετικός σταθερός αριθμός και 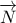 το πρώτο κάθετο της
το πρώτο κάθετο της  .
. Να αποδειχθούν τα εξής:
-

όπου το μήκος της καμπύλης
το μήκος της καμπύλης  .
. 
όπου και
και  οι αντίστοιχες καμπυλότητες των
οι αντίστοιχες καμπυλότητες των  και
και  .
.-

όπου και
και  τα εμβαδά που περικλείουν οι
τα εμβαδά που περικλείουν οι  και
και  αντίστοιχα.
αντίστοιχα.


 . Επειδή η
. Επειδή η  και συγκεκριμένα στο επίπεδο
και συγκεκριμένα στο επίπεδο  . Υπολογίζουμε
. Υπολογίζουμε

 {Θεώρημα ολικής καμπυλότητας.}
{Θεώρημα ολικής καμπυλότητας.}
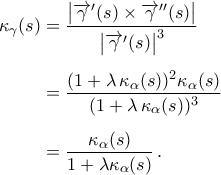
![\overrightarrow{X}: [0,L]\times[0,\lambda]\longrightarrow{\mathbb{R}}^3 \overrightarrow{X}: [0,L]\times[0,\lambda]\longrightarrow{\mathbb{R}}^3](/forum/ext/geomar/texintegr/latexrender/pictures/89b481115e33018f173c39198c8cb70d.png) με τύπο
με τύπο 
![S=\overrightarrow{X}\big({[0,L]\times[0,\lambda]}\big) S=\overrightarrow{X}\big({[0,L]\times[0,\lambda]}\big)](/forum/ext/geomar/texintegr/latexrender/pictures/d366834d5e85bbb1fd386776c71c48f4.png) το χωρίο που που περικλείουν οι
το χωρίο που που περικλείουν οι  ισούται με το εμβαδόν
ισούται με το εμβαδόν  . Υπολογίζουμε
. Υπολογίζουμε
![\begin{aligned}
A(\Omega_{\gamma})-A(\Omega_{\alpha})=A(S)&=\iint\limits_{[0,L]\times[0,\lambda]}\big|{\overrightarrow{X}_{s}\times\overrightarrow{X}_{t}}\big|\,d(s,t)\\\noalign{\vspace{0.2cm}}
&=\int_{0}^{L}\!\int_{0}^{\lambda}1+t\,\kappa_{\alpha}(s)\,dt\,ds\\\noalign{\vspace{0.2cm}}
&=\int_{0}^{L}\!\int_{0}^{\lambda}dt\,ds+\int_{0}^{L}\!\int_{0}^{\lambda}t\,\kappa_{\alpha}(s)\,dt\,ds\\\noalign{\vspace{0.2cm}}
&=\lambda\int_{0}^{L}ds+\frac{\lambda^2}{2}\int_{0}^{L}\kappa_{\alpha}(s)\,ds\\\noalign{\vspace{0.2cm}}
&=\lambda L+\frac{\lambda^2}{2}\,2\pi\\\noalign{\vspace{0.2cm}}
&=\lambda L+\lambda^2\pi\hspace{4.0cm}\Rightarrow\\\noalign{\vspace{0.2cm}}
A(\Omega_{\gamma})&=A(\Omega_{\alpha})+\lambda L+\lambda^2\pi\,.
\end{aligned} \begin{aligned}
A(\Omega_{\gamma})-A(\Omega_{\alpha})=A(S)&=\iint\limits_{[0,L]\times[0,\lambda]}\big|{\overrightarrow{X}_{s}\times\overrightarrow{X}_{t}}\big|\,d(s,t)\\\noalign{\vspace{0.2cm}}
&=\int_{0}^{L}\!\int_{0}^{\lambda}1+t\,\kappa_{\alpha}(s)\,dt\,ds\\\noalign{\vspace{0.2cm}}
&=\int_{0}^{L}\!\int_{0}^{\lambda}dt\,ds+\int_{0}^{L}\!\int_{0}^{\lambda}t\,\kappa_{\alpha}(s)\,dt\,ds\\\noalign{\vspace{0.2cm}}
&=\lambda\int_{0}^{L}ds+\frac{\lambda^2}{2}\int_{0}^{L}\kappa_{\alpha}(s)\,ds\\\noalign{\vspace{0.2cm}}
&=\lambda L+\frac{\lambda^2}{2}\,2\pi\\\noalign{\vspace{0.2cm}}
&=\lambda L+\lambda^2\pi\hspace{4.0cm}\Rightarrow\\\noalign{\vspace{0.2cm}}
A(\Omega_{\gamma})&=A(\Omega_{\alpha})+\lambda L+\lambda^2\pi\,.
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/f7883818fb598828be687ab0db024e8f.png)