Θανάση η εξίσωσηsocrates έγραψε:32)
 με παίδεψε πολύ και το μόνο που κατάφερα να βρώ ήταν η τετριμένη αυτή περίπτωση για άπειρες λύσεις και ότι οι απειρείες λύσεων τουλάχιστον μιας μεταβλητής δεν θα ήταν πολυώνυμο βαθμού μικρότερου του
με παίδεψε πολύ και το μόνο που κατάφερα να βρώ ήταν η τετριμένη αυτή περίπτωση για άπειρες λύσεις και ότι οι απειρείες λύσεων τουλάχιστον μιας μεταβλητής δεν θα ήταν πολυώνυμο βαθμού μικρότερου του  .Γιαυτό μου έκανε πολύ εντύπωση αυτή η εξίσωση και ήθελα να δω αυτό που έστειλες....Πολύ ενδιαφέρον...
.Γιαυτό μου έκανε πολύ εντύπωση αυτή η εξίσωση και ήθελα να δω αυτό που έστειλες....Πολύ ενδιαφέρον...έγινε προσθήκη εκφώνησης
Φωτεινή



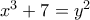


 άρα
άρα 
 ....
.... έχει έναν πρώτο διαιρέτη της αυτής μορφής.
έχει έναν πρώτο διαιρέτη της αυτής μορφής. πρώτος και
πρώτος και  και ο
και ο  τότε
τότε  .
. είναι της μορφής
είναι της μορφής  άρα αφού βλέπουμε ότι
άρα αφού βλέπουμε ότι  τελικά δεν έχουμε λύσεις...
τελικά δεν έχουμε λύσεις... και βλέπουμε ότι αν έχει λύσεις θα είναι περιττοί οι
και βλέπουμε ότι αν έχει λύσεις θα είναι περιττοί οι  και τελικά σε κάθε περίπτωση στο γινόμενο
και τελικά σε κάθε περίπτωση στο γινόμενο 
![y\left[ 2y^2+x(x-3)y+x(3x+1)\right] =0. y\left[ 2y^2+x(x-3)y+x(3x+1)\right] =0.](/forum/ext/geomar/texintegr/latexrender/pictures/f66b1d7b49ebe83775574080abfe2e0d.png)
 όπου
όπου  ακέραιος είναι λύσεις.
ακέραιος είναι λύσεις.  έχει διακρίνουσα
έχει διακρίνουσα  Για να έχουμε ακέραιες λύσεις θα πρέπει η διακρίνουσα να είναι τέλειο τετράγωνο.
Για να έχουμε ακέραιες λύσεις θα πρέπει η διακρίνουσα να είναι τέλειο τετράγωνο. Αν
Αν 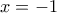 τότε
τότε 
 τότε
τότε 
 τότε
τότε  και τότε δεν έχουμε λύσεις.
και τότε δεν έχουμε λύσεις. η διακρίνουσα είναι τέλειο τετράγωνο όταν ο αριθμός
η διακρίνουσα είναι τέλειο τετράγωνο όταν ο αριθμός  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο. για κάθε
για κάθε  ή
ή 
 και τότε
και τότε  ή
ή 
 η διακρίνουσα είναι τέλειο τετράγωνο όταν ο αριθμός
η διακρίνουσα είναι τέλειο τετράγωνο όταν ο αριθμός  για κάθε
για κάθε  . Άρα για να έχουμε λύση θα πρέπει
. Άρα για να έχουμε λύση θα πρέπει 
 και όλα τα ζεύγη
και όλα τα ζεύγη 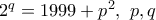 πρώτοι
πρώτοι

 δεν έχει λύσεις. Άρα
δεν έχει λύσεις. Άρα 
 .
. να συνεχίσω τον συλλογισμό μου γιατί υπάρχουν δικαίως απορίες που λόγω χρόνου δεν καλύφθηκαν.
να συνεχίσω τον συλλογισμό μου γιατί υπάρχουν δικαίως απορίες που λόγω χρόνου δεν καλύφθηκαν. για πρώτο
για πρώτο  ,
,  είναι πάντα της μορφής
είναι πάντα της μορφής 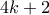 και ο άλλος της μορφής
και ο άλλος της μορφής  .Aφού
.Aφού  τότε σύμφωνα με τον έλεγχο που κάναμε ο
τότε σύμφωνα με τον έλεγχο που κάναμε ο  ή
ή  και αντικαθιστούμε τον
και αντικαθιστούμε τον 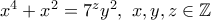
 .
.
 η ΄μέγιστη δύναη του
η ΄μέγιστη δύναη του  που διαιρεί τον
που διαιρεί τον 
 όπου
όπου  .
. 
 &
& 
 &
&  . Η πρώτη περίπτωση είναι απλή και για την δεύτερη δουλεύω
. Η πρώτη περίπτωση είναι απλή και για την δεύτερη δουλεύω  .
. είναι πολυώνυμο τετάρτου βαθμού ...(Δοκιμάζουμε και για τρίτου βαθμού.)
είναι πολυώνυμο τετάρτου βαθμού ...(Δοκιμάζουμε και για τρίτου βαθμού.) ,
,  ,
, 

 ενώ θα μπορούσε το πολυώνυμο να έχει πάνω απο
ενώ θα μπορούσε το πολυώνυμο να έχει πάνω απο  Έχει άπειρες;
Έχει άπειρες;

 περιέχει το
περιέχει το  η εξίσωση έχει τις προφανείς λύσεις
η εξίσωση έχει τις προφανείς λύσεις 
 Τότε, είναι
Τότε, είναι  άρα
άρα 


 πρώτος) ότι πρέπει το
πρώτος) ότι πρέπει το  να είναι της μορφής
να είναι της μορφής  . Οπότε, λόγω της (1), είναι
. Οπότε, λόγω της (1), είναι  Τότε εύκολα βρίσκουμε
Τότε εύκολα βρίσκουμε 


 και επειδή
και επειδή  έχουμε
έχουμε 
 .
.



 ικανοποιεί την εξίσωση.
ικανοποιεί την εξίσωση.






 πρώτος
πρώτος
 ( Προφανοί ζεύγοι λύσεων
( Προφανοί ζεύγοι λύσεων 
 είναι άρτιος.
είναι άρτιος. ,
,  .
.

 ή
ή  όμως
όμως  για κάθε
για κάθε  . Άρα δεν υπάρχουν άλλες λύσεις!
. Άρα δεν υπάρχουν άλλες λύσεις! (Προφανείς λύσεις
(Προφανείς λύσεις  )
) περιττός τότε
περιττός τότε 
 άρτιος ενώ η ποσότητα
άρτιος ενώ η ποσότητα  είναι
είναι  &
&  όμως αφού
όμως αφού  άρτιος τότε θα ισχύει ότι
άρτιος τότε θα ισχύει ότι  εκτός και αν
εκτός και αν  που μας δίνει και πάλι την λύση
που μας δίνει και πάλι την λύση  .
. .
.

 &
& 
 ,
,  ,
, .
. και έτσι κάνοντας έλεγχο βλέπουμε ότι
και έτσι κάνοντας έλεγχο βλέπουμε ότι  .
. ,
,  .
. 
 Δεδομένου ότι
Δεδομένου ότι  ,
,  &
&  θα έχουμε ότι
θα έχουμε ότι  &
&  που δεν μας δίνει καμία λύση για
που δεν μας δίνει καμία λύση για 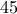 ;
; . Αν
. Αν , ή
, ή  , από Catalan πρέπει
, από Catalan πρέπει  ή
ή  . Πέρνουμε την λύση
. Πέρνουμε την λύση  .
. οπότε
οπότε  ,
,  , οπότε ο ένας από τους
, οπότε ο ένας από τους αφαιρόντας κατα μέλη:
αφαιρόντας κατα μέλη:  , οπότε πρέπει
, οπότε πρέπει  , που δεν ισχύει εκτός και αν
, που δεν ισχύει εκτός και αν . τότε όμως,
. τότε όμως,  και άρα
και άρα  . αν
. αν 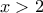 , πρέπει
, πρέπει  να είναι πολλ. του
να είναι πολλ. του  (τάξη του
(τάξη του  ) και άρα άρτιος, οπότε
) και άρα άρτιος, οπότε  ή
ή  , απ' όπου
, απ' όπου  , και
, και  .
. , αφαιρόντας κατα μέλη:
, αφαιρόντας κατα μέλη:  , οπότε πρέπει
, οπότε πρέπει  , που δεν ισχύει εκτός και αν
, που δεν ισχύει εκτός και αν , οπότε
, οπότε  , οπότε το
, οπότε το  (η τάξη του
(η τάξη του  ), κάτι που δεν γίνεται αφού είναι περιττό.
), κάτι που δεν γίνεται αφού είναι περιττό. .
. για να δεις ότι ο
για να δεις ότι ο  η εξίσωση να είναι αδύνατη εξαιρώντας τις τετριμμένες περιπτώσεις. Αν κάποιος βρεί τον
η εξίσωση να είναι αδύνατη εξαιρώντας τις τετριμμένες περιπτώσεις. Αν κάποιος βρεί τον 




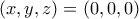
 για να δούμε ότι
για να δούμε ότι 
 .Τα ύψη ανήκουν στο σύνολο
.Τα ύψη ανήκουν στο σύνολο  των ακέραιων λύσεων.
των ακέραιων λύσεων. .
. , όμως
, όμως 


 είναι ένα στοιχείο του
είναι ένα στοιχείο του