Σκεφτόμουνα μια διαφορετική προσέγγιση.
Έστω
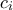 η
η 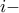 στήλη. Βλέπω ότι αν ένα
στήλη. Βλέπω ότι αν ένα  είναι λύση τότε
είναι λύση τότε 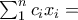

με
 την i-οστη συντεταγμένη του σταθερού διανύσματος
την i-οστη συντεταγμένη του σταθερού διανύσματος  .Αν θεωρήσω τώρα
.Αν θεωρήσω τώρα 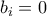 δηλαδή το αντίστοιχο ομογενές σύστημα ,παρατηρώ ότι η υπάρχει η τετριμμένη λύση και μάλιστα είναι μοναδική. Αυτό το μεταφράζω από Γενική λύση = Ειδική + Ομογενής δεν υπάρχουν ελεύθερες μεταβλητές στο αρχικό σύστημα και μάλιστα ότι καμία στήλη δεν είναι μηδενική. Άρα σε κάθε στήλη υπάρχει ένα ηγετικό στοιχείο και δεξιότερα του
δηλαδή το αντίστοιχο ομογενές σύστημα ,παρατηρώ ότι η υπάρχει η τετριμμένη λύση και μάλιστα είναι μοναδική. Αυτό το μεταφράζω από Γενική λύση = Ειδική + Ομογενής δεν υπάρχουν ελεύθερες μεταβλητές στο αρχικό σύστημα και μάλιστα ότι καμία στήλη δεν είναι μηδενική. Άρα σε κάθε στήλη υπάρχει ένα ηγετικό στοιχείο και δεξιότερα του σε κάθε γραμμή καμία ελεύθερη μεταβλητή . Αυτό αποδεικνύει την μοναδικότητα. Έστω ότι είναι ασυμβίβαστο ,τότε από Gauss το σύστημα καταλήγει σε μηδενική γραμμή με μη μηδενικό σταθερό άρα για κάποια στήλη δεν υπάρχει ηγετικό στοιχείο.
βεβαία ο πιο σύντομος δρόμος λέει αφού αντιστρέψιμος , n γραμμικά ανεξάρτητες στήλες στο
 άρα παράγουν τον χώρο άρα και το
άρα παράγουν τον χώρο άρα και το 

 έχει λύση για τετριμμένους λόγους. Να τη:
έχει λύση για τετριμμένους λόγους. Να τη: 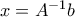 . Για τους ίδιους τετριμμένους λόγους είναι μοναδική: Αν
. Για τους ίδιους τετριμμένους λόγους είναι μοναδική: Αν 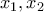 λύσεις, τότε
λύσεις, τότε 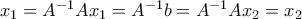 .
.  είναι μη μηδενική τότε το σύστημα έχει μοναδική λύση και αντίστροφα, ισοδύναμα, ο πίνακας είναι αντιστρέψιμος.
είναι μη μηδενική τότε το σύστημα έχει μοναδική λύση και αντίστροφα, ισοδύναμα, ο πίνακας είναι αντιστρέψιμος.