Πολλαπλασιάζουμε τη δεύτερη επίdimplak έγραψε: 1.
 και προσθέτουμε τις εξισώσεις κατά μέλη, οπότε προκύπτει
και προσθέτουμε τις εξισώσεις κατά μέλη, οπότε προκύπτει
Λύνοντας την εξίσωση βρίσκουμε
 άρα οι λύσεις του συστήματος είναι οι
άρα οι λύσεις του συστήματος είναι οι 
Συντονιστής: exdx
Πολλαπλασιάζουμε τη δεύτερη επίdimplak έγραψε: 1.
 και προσθέτουμε τις εξισώσεις κατά μέλη, οπότε προκύπτει
και προσθέτουμε τις εξισώσεις κατά μέλη, οπότε προκύπτει
 άρα οι λύσεις του συστήματος είναι οι
άρα οι λύσεις του συστήματος είναι οι 
matha έγραψε:Πολλαπλασιάζουμε τη δεύτερη επίdimplak έγραψε: 1.
και προσθέτουμε τις εξισώσεις κατά μέλη, οπότε προκύπτει
Λύνοντας την εξίσωση βρίσκουμεάρα οι λύσεις του συστήματος είναι οι
 οπότε
οπότε  και με πρόσθεση κατά μέλη προκύπτει ότι
και με πρόσθεση κατά μέλη προκύπτει ότι  . Τότε με αντικατάσταση στο αρχικό σύστημα και λύνοντας ως προς
. Τότε με αντικατάσταση στο αρχικό σύστημα και λύνοντας ως προς 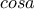 και
και  προκύπτει ότι
προκύπτει ότι  . Συνεπώς , λόγω της τριγωνομετρικής ταυτότητας
. Συνεπώς , λόγω της τριγωνομετρικής ταυτότητας  προκύπτει ότι
προκύπτει ότι  και με πράξεις καταλήγουμε στο
και με πράξεις καταλήγουμε στο  οπότε
οπότε  ή
ή  . 'Αρα με αντικατάσταση προκύπτει ότι
. 'Αρα με αντικατάσταση προκύπτει ότι  ή
ή  .
.dimplak έγραψε:14.
Προσθέτουμε τις εξισώσεις :
.

Θέτωdimplak έγραψε:15.
.
 και
και  οπότε το σύστημα γίνεται
οπότε το σύστημα γίνεται  Επειδή ισχύει
Επειδή ισχύει  έχουμε
έχουμε  . Παρατηρούμε ότι το
. Παρατηρούμε ότι το  επαληθεύει την προηγούμενη εξίσωση . Οπότε τη μετασχηματίζουμε σε
επαληθεύει την προηγούμενη εξίσωση . Οπότε τη μετασχηματίζουμε σε  και με τη βοήθεια του σχήματος Horner την για
και με τη βοήθεια του σχήματος Horner την για  την παραγοντοποιούμε σε
την παραγοντοποιούμε σε  . Το πολυώνυμο 8ου βαθμού αποδεικνύεται ότι είναι θετικό. Άρα
. Το πολυώνυμο 8ου βαθμού αποδεικνύεται ότι είναι θετικό. Άρα  οπότε
οπότε  και
και  άρα
άρα  .
.

dimplak έγραψε:22.



 είναι αδύνατη
είναι αδύνατη 
dimplak έγραψε:25.
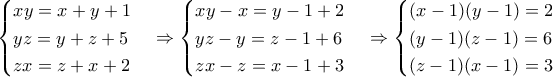

 ή
ή  , προκύπτει αδύνατο.
, προκύπτει αδύνατο. προκύπτουν
προκύπτουν  ,
, 
 προκύπτουν
προκύπτουν  ,
, 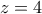 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης