ln2 < 0,699
Συντονιστής: Παύλος Μαραγκουδάκης
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
ln2 < 0,699
Με αφορμή αυτό ... προτείνω την ανισότητα του τίτλου 
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Λέξεις Κλειδιά:
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: ln2 < 0,699
Καλησπέρα. Νομίζω το παρακάτω δίνει καλύτερη εκτίμηση.
Ξεκινάμε από τη βασική ανισότητα
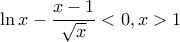 και ολοκληρώνουμε από
και ολοκληρώνουμε από  έως
έως 
Παίρνουμε:
![\left [ x\ln x-x \right ]_{1}^{2}< \left [ \dfrac{2x^{3/2}}{3}-2x^{1/2}\right ]_{1}^{2} \left [ x\ln x-x \right ]_{1}^{2}< \left [ \dfrac{2x^{3/2}}{3}-2x^{1/2}\right ]_{1}^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/227bfd73abf0249a307a87755661483c.png)
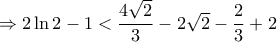
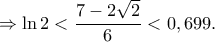
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: ln2 < 0,699
Λάμπρο πολύ ωραία, πράγματι κατέβασες το άνω φράγμα στο 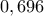 'περίπου'! Με μία μικρή 'επέκταση' της μεθόδου μου πιάνω
'περίπου'! Με μία μικρή 'επέκταση' της μεθόδου μου πιάνω 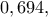 υποθέτω πως κάτι ανάλογο θα συμβαίνει και με την δική σου μέθοδο. Θα επανέλθω αργότερα, αναμένοντας και άλλες λύσεις.
υποθέτω πως κάτι ανάλογο θα συμβαίνει και με την δική σου μέθοδο. Θα επανέλθω αργότερα, αναμένοντας και άλλες λύσεις.
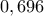 'περίπου'! Με μία μικρή 'επέκταση' της μεθόδου μου πιάνω
'περίπου'! Με μία μικρή 'επέκταση' της μεθόδου μου πιάνω 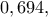 υποθέτω πως κάτι ανάλογο θα συμβαίνει και με την δική σου μέθοδο. Θα επανέλθω αργότερα, αναμένοντας και άλλες λύσεις.
υποθέτω πως κάτι ανάλογο θα συμβαίνει και με την δική σου μέθοδο. Θα επανέλθω αργότερα, αναμένοντας και άλλες λύσεις.
τελευταία επεξεργασία από gbaloglou σε Πέμ Δεκ 28, 2023 7:36 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: ln2 < 0,699
Ας το πάμε παρακάτω. Μπορούμε να χρησιμοποιήσουμε τη μέθοδο που έβαλα στην παραπομπή.
Είναι
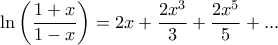
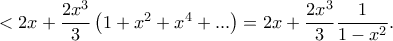
Αν θέσουμε
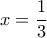 στην τελευταία ανισότητα παίρνουμε:
στην τελευταία ανισότητα παίρνουμε: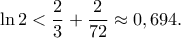 (προσέγγιση με δύο μόνο κλάσματα!)
(προσέγγιση με δύο μόνο κλάσματα!)Ακόμα καλύτερα:

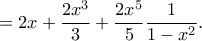
Θέτουμε
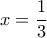 και παίρνουμε:
και παίρνουμε: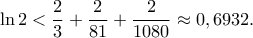 (προσέγγιση με τρια μόνο κλάσματα!)
(προσέγγιση με τρια μόνο κλάσματα!)- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: ln2 < 0,699
Λάμπρο πολύ ωραία!
Ιδού η αρχική μου προσέγγιση:
Θέτοντας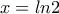 στην 'ημισχολική' ανισότητα
στην 'ημισχολική' ανισότητα 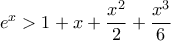 (που προκύπτει με δύο ολοκληρώσεις από την
(που προκύπτει με δύο ολοκληρώσεις από την 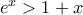 ) ... λαμβάνουμε την ανισότητα
) ... λαμβάνουμε την ανισότητα 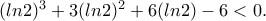 Επειδή η συνάρτηση
Επειδή η συνάρτηση 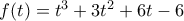 είναι προφανώς αύξουσα για
είναι προφανώς αύξουσα για 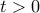 (στην πραγματικότητα παντού), αρκεί για την
(στην πραγματικότητα παντού), αρκεί για την 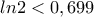 να δειχθεί η
να δειχθεί η 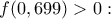 αυτό γίνεται εύκολα με το χέρι -- κατά την διάρκεια του πρωινού τσαγιού στην πραγματικότητα -- και προκύπτει η
αυτό γίνεται εύκολα με το χέρι -- κατά την διάρκεια του πρωινού τσαγιού στην πραγματικότητα -- και προκύπτει η 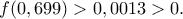 [Αναφέρω απλώς ότι
[Αναφέρω απλώς ότι 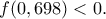 ]
]
Αν τώρα χρησιμοποιήσουμε την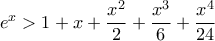 με τον ίδιο τρόπο, πάλι με το χέρι βρίσκουμε
με τον ίδιο τρόπο, πάλι με το χέρι βρίσκουμε 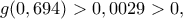 όπου
όπου 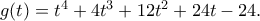 (Ουσιαστικά το άνω φράγμα είναι η ρίζα του πολυωνύμου,
(Ουσιαστικά το άνω φράγμα είναι η ρίζα του πολυωνύμου, 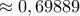 στην περίπτωση της
στην περίπτωση της  και
και 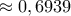 στην περίπτωση της
στην περίπτωση της  )
)
Αναλόγως η μέθοδος μου μπορεί να δώσει και πιο σφικτά άνω φράγματα, μειονεκτεί όμως έναντι της μεθόδου του Λάμπρου, αν μη τι άλλο επειδή είναι πολύ πιο δύσκολο να υπολογισθεί εκ των προτέρων 'πόσους όρους' χρειαζόμαστε για 'δεδομένο' άνω φράγμα. (Ίσως επανέλθω επ' αυτού αργότερα.)
Ιδού η αρχική μου προσέγγιση:
Θέτοντας
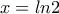 στην 'ημισχολική' ανισότητα
στην 'ημισχολική' ανισότητα 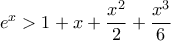 (που προκύπτει με δύο ολοκληρώσεις από την
(που προκύπτει με δύο ολοκληρώσεις από την 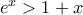 ) ... λαμβάνουμε την ανισότητα
) ... λαμβάνουμε την ανισότητα 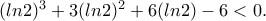 Επειδή η συνάρτηση
Επειδή η συνάρτηση 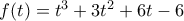 είναι προφανώς αύξουσα για
είναι προφανώς αύξουσα για 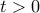 (στην πραγματικότητα παντού), αρκεί για την
(στην πραγματικότητα παντού), αρκεί για την 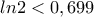 να δειχθεί η
να δειχθεί η 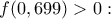 αυτό γίνεται εύκολα με το χέρι -- κατά την διάρκεια του πρωινού τσαγιού στην πραγματικότητα -- και προκύπτει η
αυτό γίνεται εύκολα με το χέρι -- κατά την διάρκεια του πρωινού τσαγιού στην πραγματικότητα -- και προκύπτει η 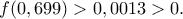 [Αναφέρω απλώς ότι
[Αναφέρω απλώς ότι 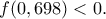 ]
]Αν τώρα χρησιμοποιήσουμε την
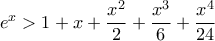 με τον ίδιο τρόπο, πάλι με το χέρι βρίσκουμε
με τον ίδιο τρόπο, πάλι με το χέρι βρίσκουμε 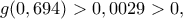 όπου
όπου 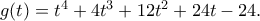 (Ουσιαστικά το άνω φράγμα είναι η ρίζα του πολυωνύμου,
(Ουσιαστικά το άνω φράγμα είναι η ρίζα του πολυωνύμου, 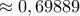 στην περίπτωση της
στην περίπτωση της  και
και 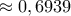 στην περίπτωση της
στην περίπτωση της 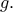 )
)Αναλόγως η μέθοδος μου μπορεί να δώσει και πιο σφικτά άνω φράγματα, μειονεκτεί όμως έναντι της μεθόδου του Λάμπρου, αν μη τι άλλο επειδή είναι πολύ πιο δύσκολο να υπολογισθεί εκ των προτέρων 'πόσους όρους' χρειαζόμαστε για 'δεδομένο' άνω φράγμα. (Ίσως επανέλθω επ' αυτού αργότερα.)
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: ln2 < 0,699
Όχι ακριβώς, η 'πρόβλεψη' δεν είναι εύκολη υπόθεση ούτε στην μία μέθοδο ούτε στην άλλη. Απλώς η μέθοδος του Λάμπρου υπερτερεί επειδή μας δίνει μία ακολουθία αθροισμάτων κλασμάτων που συγκλίνει εκ των άνω στονgbaloglou έγραψε: ↑Πέμ Δεκ 28, 2023 7:30 pmΑναλόγως η μέθοδος μου μπορεί να δώσει και πιο σφικτά άνω φράγματα, μειονεκτεί όμως έναντι της μεθόδου του Λάμπρου, αν μη τι άλλο επειδή είναι πολύ πιο δύσκολο να υπολογισθεί εκ των προτέρων 'πόσους όρους' χρειαζόμαστε για 'δεδομένο' άνω φράγμα. (Ίσως επανέλθω επ' αυτού αργότερα.)
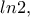 ενώ η δική μου μέθοδος μας δίνει μία ακολουθία πολυωνύμων των οποίων η μεγαλύτερη ρίζα επίσης συγκλίνει εκ των άνω στον
ενώ η δική μου μέθοδος μας δίνει μία ακολουθία πολυωνύμων των οποίων η μεγαλύτερη ρίζα επίσης συγκλίνει εκ των άνω στον 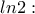 και τα κλάσματα του Λάμπρου και τα πολυώνυμα μου είναι πολύ προσιτά και συγκεκριμένα, στην δική μου όμως μέθοδο έχουμε να βρούμε/προσεγγίσουμε ρίζες πολυωνύμων, ενώ στην μέθοδο του Λάμπρου απλώς να αθροίσουμε κλάσματα.
και τα κλάσματα του Λάμπρου και τα πολυώνυμα μου είναι πολύ προσιτά και συγκεκριμένα, στην δική μου όμως μέθοδο έχουμε να βρούμε/προσεγγίσουμε ρίζες πολυωνύμων, ενώ στην μέθοδο του Λάμπρου απλώς να αθροίσουμε κλάσματα.Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Re: ln2 < 0,699
Καλησπέρα.
Ας παρατηρηθεί ότι από το συνεχές κλάσμα που αναφέρεται στην παραπομπή, μπορούμε να πάρουμε και την από πάνω προσέγγιση
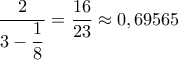 .
.
Το αναφέρω, για να υπάρχει σαν πληροφορία.
Ας παρατηρηθεί ότι από το συνεχές κλάσμα που αναφέρεται στην παραπομπή, μπορούμε να πάρουμε και την από πάνω προσέγγιση
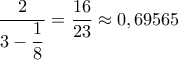 .
.Το αναφέρω, για να υπάρχει σαν πληροφορία.
Κώστας
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
