![\int_{1}^{\lambda-2} t [ \frac{\log(\lambda - t)}{\log 2}] dt \int_{1}^{\lambda-2} t [ \frac{\log(\lambda - t)}{\log 2}] dt](/forum/ext/geomar/texintegr/latexrender/pictures/78d6c65b082e676d0d3fad6f9503b1ac.png) , όπου
, όπου 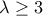 .
.Εδώ τα
![[ .. ] [ .. ]](/forum/ext/geomar/texintegr/latexrender/pictures/f4c4388b0360424d0454cfcc0047c5b8.png) συμβολίζουν το ακέραιο μέρος(integer part).
συμβολίζουν το ακέραιο μέρος(integer part).Το χρειάζομαι στην έρευνά μου.
Ευχαριστώ.
Edit:Φυσικά θα γίνει αναφορά σε όποιον με βοηθήσει(academic integrity)
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![\int_{1}^{\lambda-2} t [ \frac{\log(\lambda - t)}{\log 2}] dt \int_{1}^{\lambda-2} t [ \frac{\log(\lambda - t)}{\log 2}] dt](/forum/ext/geomar/texintegr/latexrender/pictures/78d6c65b082e676d0d3fad6f9503b1ac.png) , όπου
, όπου 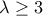 .
.![[ .. ] [ .. ]](/forum/ext/geomar/texintegr/latexrender/pictures/f4c4388b0360424d0454cfcc0047c5b8.png) συμβολίζουν το ακέραιο μέρος(integer part).
συμβολίζουν το ακέραιο μέρος(integer part).Μία ιδέα, που νομίζω βγάζει αποτέλεσμα.
 η σχέση
η σχέση ![\left [\frac{\log(\lambda - t)}{\log 2}\right ] = n \left [\frac{\log(\lambda - t)}{\log 2}\right ] = n](/forum/ext/geomar/texintegr/latexrender/pictures/161c567c449d243f5fd4a8eded07c713.png) ανν
ανν ![n \le \left [\frac{\log(\lambda - t)}{\log 2}\right ] < n+1 n \le \left [\frac{\log(\lambda - t)}{\log 2}\right ] < n+1](/forum/ext/geomar/texintegr/latexrender/pictures/27072fb08597942a2ba2455134aed508.png) ανν
ανν 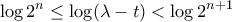 ανν
ανν 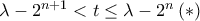
 (εδώ
(εδώ  το μεγαλύτερο δυνατό).
το μεγαλύτερο δυνατό).  έχουμε
έχουμε ![\displaystyle{ \int _{\lambda - 2^{p+1}}^{\lambda - 2^{p}} t \left [ \frac{\log(\lambda - t)}{\log 2} \right ] dt = \int _{\lambda - 2^{p+1}}^{\lambda - 2^{p}} t p dt = \dfrac {p}{2} \left ( \left ( \lambda - 2^{p}) ^2 - \left ( \lambda - 2^{p+1}) ^2 \right )=} \displaystyle{ \int _{\lambda - 2^{p+1}}^{\lambda - 2^{p}} t \left [ \frac{\log(\lambda - t)}{\log 2} \right ] dt = \int _{\lambda - 2^{p+1}}^{\lambda - 2^{p}} t p dt = \dfrac {p}{2} \left ( \left ( \lambda - 2^{p}) ^2 - \left ( \lambda - 2^{p+1}) ^2 \right )=}](/forum/ext/geomar/texintegr/latexrender/pictures/538893ba92be1a17813ff696b6086849.png)
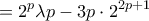
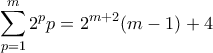 και
και 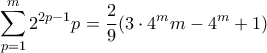 (ελπίζω να έκανα σωστά τις πράξεις, αλλά ... κάπου εκεί είναι το σωστό).
(ελπίζω να έκανα σωστά τις πράξεις, αλλά ... κάπου εκεί είναι το σωστό).Μια απόπειρα...
 αντί
αντί  και όπου
και όπου 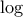 εννοώ αναφέρομαι σε νεπέριο λογάριθμο (φυσικά δεν έχει διαφορά αν είναι δεκαδικός στην εκφώνηση μιας και εμφανίζεται λόγος λογαρίθμων)
εννοώ αναφέρομαι σε νεπέριο λογάριθμο (φυσικά δεν έχει διαφορά αν είναι δεκαδικός στην εκφώνηση μιας και εμφανίζεται λόγος λογαρίθμων)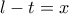 :
: 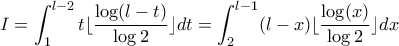
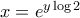 :
: 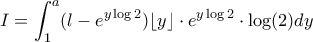 όπου έθεσα
όπου έθεσα 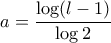 .
. 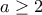
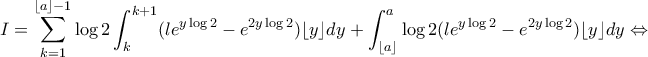
![I=\displaystyle \sum_{k=1}^{\lfloor a \rfloor-1}k \log 2 [\dfrac{1}{\log 2}\cdot le^{y\log2}-\dfrac{1}{2 \log 2}\cdot e^{2y\log2}]^{k+1}_{k}+\lfloor a \rfloor \log 2[\dfrac{1}{\log 2}\cdot le^{y\log2}-\dfrac{1}{2 \log 2}\cdot e^{2y\log2}]^{a}_{\lfloor a \rfloor}\Leftrightarrow I=\displaystyle \sum_{k=1}^{\lfloor a \rfloor-1}k \log 2 [\dfrac{1}{\log 2}\cdot le^{y\log2}-\dfrac{1}{2 \log 2}\cdot e^{2y\log2}]^{k+1}_{k}+\lfloor a \rfloor \log 2[\dfrac{1}{\log 2}\cdot le^{y\log2}-\dfrac{1}{2 \log 2}\cdot e^{2y\log2}]^{a}_{\lfloor a \rfloor}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/a37a2d9558515a772723be58f5625539.png)
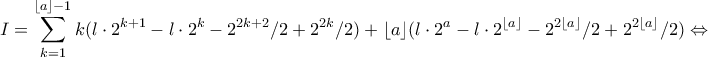
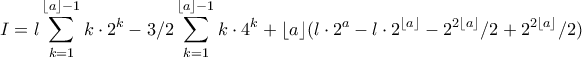

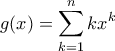 , και
, και 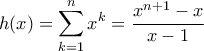 παρατηρούμε ότι
παρατηρούμε ότι 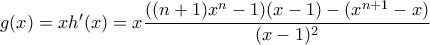 οπότε με
οπότε με 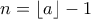 θα είναι
θα είναι 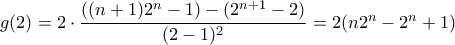
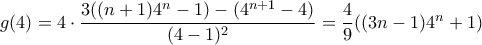
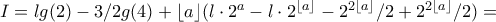
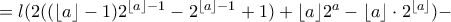
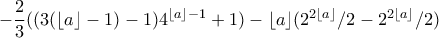
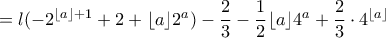
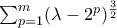 ,
,![m=[\frac{\log (\lambda -1)}{\log 2}] m=[\frac{\log (\lambda -1)}{\log 2}]](/forum/ext/geomar/texintegr/latexrender/pictures/06cd7f4a9fb94ed4d4119d52cc134884.png) και
και ![[.] [.]](/forum/ext/geomar/texintegr/latexrender/pictures/d0b10a15db40a36d59fddb83ef024cf2.png) το ακέραιο μέρος.
το ακέραιο μέρος. εννοείται).
εννοείται).Για μεγάλα
 το άθροισμα πάει στο
το άθροισμα πάει στο 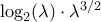 .
.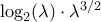 είναι άνω φράγμα είναι φανερό μιας και
είναι άνω φράγμα είναι φανερό μιας και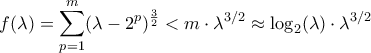
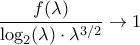 βγαίνει ως εξής:
βγαίνει ως εξής: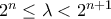 , τότε
, τότε 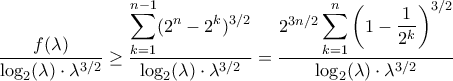 .
. το
το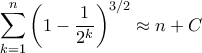 και έτσι
και έτσι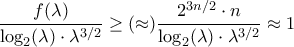
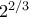 αλλά μιας και μιλάμε χοντρικά νομίζω δεν υπάρχει πρόβλημα)
αλλά μιας και μιλάμε χοντρικά νομίζω δεν υπάρχει πρόβλημα)
Είσαι ωραίος.ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑Δευ Ιαν 29, 2024 8:00 pmΓια μεγάλατο άθροισμα πάει στο
.
Αρχικά το ότιείναι άνω φράγμα είναι φανερό μιας και
Τώρα το ότι τοβγαίνει ως εξής:
Έστω, τότε
.
Για μεγάλατο
και έτσι
(το τελευταίο βήμα ίσως δεν φαίνεται τόσο αυστηρό μιας και θα μπορούσε να εμφανιστεί ίσως και κάποια σταθερά του τύπουαλλά μιας και μιλάμε χοντρικά νομίζω δεν υπάρχει πρόβλημα)
Τέλος εδώ είναι μια γραφική παράσταση της
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες