Πρόβλημα 1
Να λυθεί στους πραγματικούς η εξίσωση:

Πρόβλημα 2
Δίνεται ημικύκλιο ακτίνας
 με κέντρο
με κέντρο  και με άκρα
και με άκρα  , και
, και 
σημείο τέτοιο ώστε το
 να είναι ισόπλευρο και το ημικύκλιο με το
να είναι ισόπλευρο και το ημικύκλιο με το 
να βρίσκονται εκατέρωθεν της
 . Στην συνέχεια, παίρνουμε σημείο
. Στην συνέχεια, παίρνουμε σημείο 
στην
 τέτοιο ώστε
τέτοιο ώστε  . Αν
. Αν  είναι το σημείο τομής
είναι το σημείο τομήςτης καθέτου από το
 ως προς την
ως προς την  με το ημικύκλιο, και
με το ημικύκλιο, και  σημείο της
σημείο της 
έτσι ώστε το
 να είναι εγγράψιμο, να βρεθεί το εμβαδόν του χωρίου
να είναι εγγράψιμο, να βρεθεί το εμβαδόν του χωρίουπου περικλείεται από τις πλευρές
 και το τόξο
και το τόξο  συναρτήσει του
συναρτήσει του  .
.Πρόβλημα 3
Αν ο
 είναι θετικός ακέραιος και
είναι θετικός ακέραιος και  οι θετικοί ακέραιοι
οι θετικοί ακέραιοιδιαιρέτες του με
 . Να βρεθούν όλα τα ζεύγη
. Να βρεθούν όλα τα ζεύγη  που
πουικανοποιούν την εξίσωση:

Πρόβλημα 4
α) Να λυθεί στους πραγματικούς η εξίσωση:

β) Να βρείτε
 πραγματικούς αριθμούς
πραγματικούς αριθμούς  με
με  για τους οποίους ο αριθμός:
για τους οποίους ο αριθμός:
παίρνει την ίδια τιμή για
 και
και  καθώς και την τιμή που παίρνει.
καθώς και την τιμή που παίρνει.
 .
. συνεπώς ειναι άρτιος.
συνεπώς ειναι άρτιος.  άρα
άρα  .
. οπότε παίρνουμε
οπότε παίρνουμε  .
.
 , όπου η κάθε παρένθεση είναι προφανώς άρτιος.
, όπου η κάθε παρένθεση είναι προφανώς άρτιος. ως διαιρέτης του.
ως διαιρέτης του. , οπότε
, οπότε  .
. και από εδώ με αντικατάσταση στην
και από εδώ με αντικατάσταση στην  .
. .
. (ισοδυναμεί με την αληθή
(ισοδυναμεί με την αληθή  ).
). .
. , που δίνει
, που δίνει  , που επαληθεύει.
, που επαληθεύει. .
. .
. (1),
(1),  (2) και
(2) και  (3).
(3). .
. παράγοντα και απλοποίηση του όρου αυτού (αφού είναι μη μηδενικός) παίρνουμε
παράγοντα και απλοποίηση του όρου αυτού (αφού είναι μη μηδενικός) παίρνουμε  (4)
(4) (5)
(5) και οι (4), (5) γίνονται
και οι (4), (5) γίνονται  και
και  , με λύση
, με λύση  .
. , οπότε τα
, οπότε τα  , που από το α), έχει ρίζες τις
, που από το α), έχει ρίζες τις  .
. και
και  .
. και
και  καταλήγουμε σε μία αληθή ισότητα.
καταλήγουμε σε μία αληθή ισότητα. , με τον περιορισμό
, με τον περιορισμό  (γιατί;).
(γιατί;). .
.
 .
. .
. .
. .
. το εμβαδόν του ημικυκλίου με διάμετρο την
το εμβαδόν του ημικυκλίου με διάμετρο την 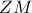 , που περιέχει το
, που περιέχει το  .
. το εμβαδόν του κυκλικού τμήματος
το εμβαδόν του κυκλικού τμήματος  .
. .
. (1).
(1). , οπότε
, οπότε  (2).
(2). .
.
 τότε
τότε  και
και 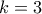

 , όπου
, όπου 


![x^{3}-7x^{2}+7x=x(x^{2}-7x+7)=x(x^{2}-6x+1-x+6)\Rightarrow x^{3}-7x^{2}+7x=x[(x^{2}-6x+1)-(x+6)] x^{3}-7x^{2}+7x=x(x^{2}-7x+7)=x(x^{2}-6x+1-x+6)\Rightarrow x^{3}-7x^{2}+7x=x[(x^{2}-6x+1)-(x+6)]](/forum/ext/geomar/texintegr/latexrender/pictures/2561af65a7b433f6dceeb4231a5cbaea.png) (1)
(1)![x^{3}-5x^{2}-5x=x(x^{2}-5x-5)=x[(x^{2}-6x+1)+(x-6)] x^{3}-5x^{2}-5x=x(x^{2}-5x-5)=x[(x^{2}-6x+1)+(x-6)]](/forum/ext/geomar/texintegr/latexrender/pictures/81760b18816c44e724392cf39809230b.png) (2)
(2)![x^{4}-6x^{3}+6x=x(x^{3}-6x^{2}+6)=x[x (x^{2}-6x+1)-(x-6)] x^{4}-6x^{3}+6x=x(x^{3}-6x^{2}+6)=x[x (x^{2}-6x+1)-(x-6)]](/forum/ext/geomar/texintegr/latexrender/pictures/bb50b78cdb92e60cf53e4dec11f5caba.png) (3)
(3)![A=\frac{x[(x^{2}-6x+1)^{2}-(x-6)^{2}]}{x(x^{2}-6x+1)-(x-6)} A=\frac{x[(x^{2}-6x+1)^{2}-(x-6)^{2}]}{x(x^{2}-6x+1)-(x-6)}](/forum/ext/geomar/texintegr/latexrender/pictures/761fb9a681aac2e9de49a89a850d2384.png)




 για
για