 την εξίσωση
την εξίσωση 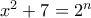
Συντονιστής: nkatsipis

 , οπότε από την αρχική εξίσωση παίρνουμε την παρακάτω:
, οπότε από την αρχική εξίσωση παίρνουμε την παρακάτω: , προφανώς το
, προφανώς το  πρέπει να είναι περιττός.
πρέπει να είναι περιττός. , μετά από τις πράξεις καταλήγουμε ότι:
, μετά από τις πράξεις καταλήγουμε ότι: , Triangular Mersenne numbers
, Triangular Mersenne numbers ,
,  να επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
να επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
 είναι άρτιος, τότε
είναι άρτιος, τότε  , οπότε
, οπότε  .
.
 συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός  .
.
 είναι άρτιος, τότε
είναι άρτιος, τότε 
 είναι περιττός, τότε
είναι περιττός, τότε 
 είναι περιττός, τότε
είναι περιττός, τότε  , οπότε
, οπότε  .
.
 συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
συστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός  .
.
 είναι άρτιος, τότε
είναι άρτιος, τότε 
 είναι περιττός, τότε
είναι περιττός, τότε 
 έτσι, ώστε να λάβουμε την μορφή που θα έχει ο αριθμός
έτσι, ώστε να λάβουμε την μορφή που θα έχει ο αριθμός  σε κάθε περίπτωση;
σε κάθε περίπτωση;Nikitas K. έγραψε: ↑Δευ Απρ 22, 2024 4:00 pm,
Έστω, η συνάρτησηνα επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
- Αν
είναι άρτιος, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
- Αν
είναι περιττός, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
Δεν είμαι σίγουρος ότι βγαίνει έτσι αυτή η διοφαντική.Nikitas K. έγραψε: ↑Σάβ Απρ 27, 2024 12:07 pmΧαίρετε,
Έχοντας φτάσει ως το παρακάτω σημείο, υπάρχει κάποιος τρόπος να συνεχίστεί ο υπολογισμός όλων των δυαδικών ψηφίων του αριθμούέτσι, ώστε να λάβουμε την μορφή που θα έχει ο αριθμός
σε κάθε περίπτωση;
Nikitas K. έγραψε: ↑Δευ Απρ 22, 2024 4:00 pm,
Έστω, η συνάρτησηνα επιστρέφει το πλήθος των ψηφίων της δυαδικής αναπαράστασης της εισόδου.
- Αν
είναι άρτιος, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
- Αν
είναι περιττός, τότε
, οπότε
.
Θέτω,
Επιλύοντας τασυστήματα κάθε περίπτωσης, γίνεται να αποτιμηθεί ο αριθμός
.
- Αν
είναι άρτιος, τότε
- Αν
είναι περιττός, τότε
Ας γράψω τι σκέφτηκα, αλλα δεν έχω και πολύ χρόνο να το αναλύσω, το αφήνω ως ιδέα μήπως προχωρήσει κάπως.
 άρτιο είναι σχετικά απλό (διαφορά τετραγώνων).
άρτιο είναι σχετικά απλό (διαφορά τετραγώνων). περιττό έχουμε:
περιττό έχουμε:
 , τότε απλά τη γράφουμε στη μορφή:
, τότε απλά τη γράφουμε στη μορφή: , σαφώς με τις κατάλληλες υποθέσεις.
, σαφώς με τις κατάλληλες υποθέσεις. , μία ας τη θεωρήσουμε πρωταρχική λύση των εξισώσεων
, μία ας τη θεωρήσουμε πρωταρχική λύση των εξισώσεων  .
. έχει λύση
έχει λύση 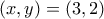

 . Μάλλον λίγο ζόρι να βρούμε πρωταρχική λύση εδώ για να πάρουμε μετά τον αναδρομικό αλγόριθμο.
. Μάλλον λίγο ζόρι να βρούμε πρωταρχική λύση εδώ για να πάρουμε μετά τον αναδρομικό αλγόριθμο. .
.![Z[i\sqrt{2}] Z[i\sqrt{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/44a8940c6a2c607d2ef0d7aa02bc147c.png) είναι UFD, το παραπάνω βέβαια είναι στο
είναι UFD, το παραπάνω βέβαια είναι στο ![Z[\sqrt{2}] Z[\sqrt{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/b42c028445420661476d1cf765e4cae5.png) , και δεν είμαι σίγουρος αν μπορούμε να δουλέψουμε ανάλογα (το 7 μάλιστα δεν είναι πρώτος σε αυτό τον δακτύλιο). Έχω την εντύπωση πως ο τελευταίος δακτύλιος είναι UFD, αν ισχύουν αυτά μπορώ να προχωρήσω σε λύση, αλλιώς μάλλον πρέπει να αλλάξουμε προσέγγιση.
, και δεν είμαι σίγουρος αν μπορούμε να δουλέψουμε ανάλογα (το 7 μάλιστα δεν είναι πρώτος σε αυτό τον δακτύλιο). Έχω την εντύπωση πως ο τελευταίος δακτύλιος είναι UFD, αν ισχύουν αυτά μπορώ να προχωρήσω σε λύση, αλλιώς μάλλον πρέπει να αλλάξουμε προσέγγιση.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες