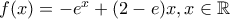 με τη γραφική παράσταση της αντίστροφής της,
με τη γραφική παράσταση της αντίστροφής της, 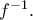
Δεν έχω λύση...
Συντονιστής: emouroukos
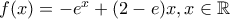 με τη γραφική παράσταση της αντίστροφής της,
με τη γραφική παράσταση της αντίστροφής της, 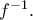
 όσο και η
όσο και η  είναι φθίνουσες και κοίλες: πράγματι,
είναι φθίνουσες και κοίλες: πράγματι, 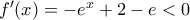 ,
,  ,
, ![[f^{-1}(x)]'=\dfrac{1}{f'(f^{-1}(x))}<0 [f^{-1}(x)]'=\dfrac{1}{f'(f^{-1}(x))}<0](/forum/ext/geomar/texintegr/latexrender/pictures/a5aefb4a2083b3f04b1ebbc585d31b89.png) ,
, ![[f^{-1}(x)]''=-\dfrac{f''(f^{-1}(x))}{[f'(f^{-1}(x))]^3}<0 [f^{-1}(x)]''=-\dfrac{f''(f^{-1}(x))}{[f'(f^{-1}(x))]^3}<0](/forum/ext/geomar/texintegr/latexrender/pictures/4125079d0736e305990fda0a227d066f.png) .
. και
και  , αρκεί να δείξουμε ότι υπάρχει ακριβώς ένα σημείο τομής επί της διαγωνίου
, αρκεί να δείξουμε ότι υπάρχει ακριβώς ένα σημείο τομής επί της διαγωνίου  , αρκεί δηλαδή να δείξουμε ότι υπάρχει ακριβώς ένα σημείο τομής της
, αρκεί δηλαδή να δείξουμε ότι υπάρχει ακριβώς ένα σημείο τομής της  με την διαγώνιο. Η εξίσωση
με την διαγώνιο. Η εξίσωση  είναι ισοδύναμη προς την
είναι ισοδύναμη προς την  , όπου
, όπου 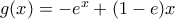 : από τις
: από τις 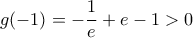 και
και 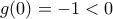 συμπεραίνουμε ότι υπάρχει τουλάχιστον ένα σημείο μηδενισμού της
συμπεραίνουμε ότι υπάρχει τουλάχιστον ένα σημείο μηδενισμού της  , και από την
, και από την 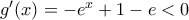 συμπεραίνουμε ότι αυτό είναι μοναδικό.
συμπεραίνουμε ότι αυτό είναι μοναδικό. εκτός της διαγωνίου; Αυτό είναι γενικά δυνατόν, ακόμη και όταν οι
εκτός της διαγωνίου; Αυτό είναι γενικά δυνατόν, ακόμη και όταν οι  είναι φθίνουσες και κοίλες, όπως εδώ. Στο συγκεκριμένο όμως πρόβλημα η ύπαρξη περισσοτέρων σημείων τομής των
είναι φθίνουσες και κοίλες, όπως εδώ. Στο συγκεκριμένο όμως πρόβλημα η ύπαρξη περισσοτέρων σημείων τομής των  αποκλείεται από το γεγονός ότι η
αποκλείεται από το γεγονός ότι η 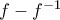 είναι φθίνουσα, όπως θα δείξουμε παρακάτω.
είναι φθίνουσα, όπως θα δείξουμε παρακάτω.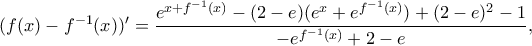
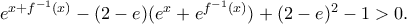
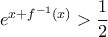 και
και 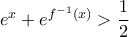 , αναγόμενη στην ισχύουσα
, αναγόμενη στην ισχύουσα 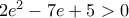 .
.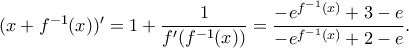
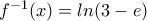 , οπότε
, οπότε 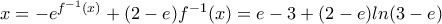 και, τελικά,
και, τελικά, 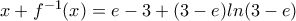 : συμπεραίνουμε ότι
: συμπεραίνουμε ότι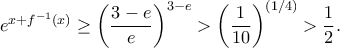
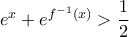 . Η ανισότητα αυτή είναι άμεση είτε στην περίπτωση
. Η ανισότητα αυτή είναι άμεση είτε στην περίπτωση  είτε στην περίπτωση
είτε στην περίπτωση 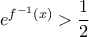 . Υποθέτοντας ότι αποτυγχάνουν και οι δύο ταυτόχρονα για κάποιο
. Υποθέτοντας ότι αποτυγχάνουν και οι δύο ταυτόχρονα για κάποιο  , οπότε
, οπότε 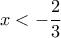 και
και 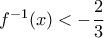 , καταλήγουμε σε άτοπο:
, καταλήγουμε σε άτοπο: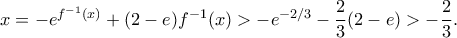
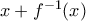 που υπολογίστηκε παραπάνω ... δεν είναι ολικό ελάχιστο αλλά ... ολικό μέγιστο!
που υπολογίστηκε παραπάνω ... δεν είναι ολικό ελάχιστο αλλά ... ολικό μέγιστο!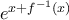 δεν είχε καν ληφθεί υπ' όψιν -- ελπίζω να επανέλθω!]
δεν είχε καν ληφθεί υπ' όψιν -- ελπίζω να επανέλθω!]Ως εδώ καλά, από εδώ και πέρα χρειάζεται -- όπως τόνισα στην αμέσως προηγούμενη δημοσίευση -- αλλαγή πλεύσης:gbaloglou έγραψε: ↑Κυρ Σεπ 25, 2022 10:46 pmΈνα και μόνον σημείο τομής, επί της διαγωνίου:
Ας παρατηρήσουμε αρχικά ότι τόσο ηόσο και η
είναι φθίνουσες και κοίλες: πράγματι,
,
,
,
.
Για να δείξουμε ότι υπάρχει τουλάχιστον ένα σημείο τομής τωνκαι
, αρκεί να δείξουμε ότι υπάρχει ακριβώς ένα σημείο τομής επί της διαγωνίου
, αρκεί δηλαδή να δείξουμε ότι υπάρχει ακριβώς ένα σημείο τομής της
με την διαγώνιο. Η εξίσωση
είναι ισοδύναμη προς την
, όπου
: από τις
και
συμπεραίνουμε ότι υπάρχει τουλάχιστον ένα σημείο μηδενισμού της
, και από την
συμπεραίνουμε ότι αυτό είναι μοναδικό.
Υπάρχουν σημεία τομής τωνεκτός της διαγωνίου; Αυτό είναι γενικά δυνατόν, ακόμη και όταν οι
είναι φθίνουσες και κοίλες, όπως εδώ. Στο συγκεκριμένο όμως πρόβλημα η ύπαρξη περισσοτέρων σημείων τομής των
αποκλείεται από το γεγονός ότι η
είναι φθίνουσα, όπως θα δείξουμε παρακάτω.
Καθώς
και ο παρονομαστής είναι μονίμως αρνητικός, αρκεί να δειχθεί η ανισότητα
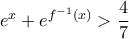 τότε
τότε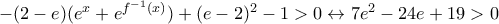 (ισχύει).
(ισχύει).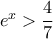 είτε η
είτε η 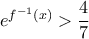 : όπως θα δούμε, αν δεν ισχύει η πρώτη ανισότητα ισχύει υποχρεωτικά η δεύτερη. Όντως, η πρώτη ανισότητα ισχύει για
: όπως θα δούμε, αν δεν ισχύει η πρώτη ανισότητα ισχύει υποχρεωτικά η δεύτερη. Όντως, η πρώτη ανισότητα ισχύει για  , ας υποθέσουμε λοιπόν
, ας υποθέσουμε λοιπόν 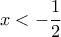 , οπότε
, οπότε 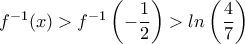 : πράγματι αν
: πράγματι αν 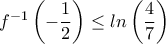 τότε
τότε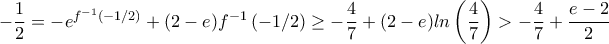 , άτοπο.
, άτοπο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες