Να υπολογιστεί το
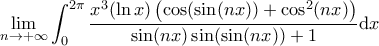
(Ελεγμένο, δεν υπάρχει τυπογραφικό!)
Συντονιστής: Demetres
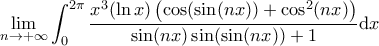
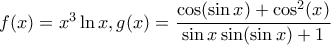 και ζητάμε το όριο του
και ζητάμε το όριο του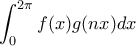 . Από γνωστό λήμμα (το έχουμε δει εδώ στο
. Από γνωστό λήμμα (το έχουμε δει εδώ στο  είναι περιοδική με περίοδο
είναι περιοδική με περίοδο 
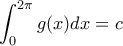 τότε
τότε 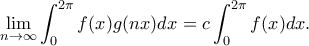
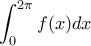 είναι μια απλή παραγοντική και δίνει
είναι μια απλή παραγοντική και δίνει 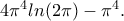
 με ζόρισε. Είναι αλεξίσφαιρο (δεν το υπολογίζει αναλυτικά ούτε το wolpram). Τελικά κατάφερα να το υπολογίσω και κάνει
με ζόρισε. Είναι αλεξίσφαιρο (δεν το υπολογίζει αναλυτικά ούτε το wolpram). Τελικά κατάφερα να το υπολογίσω και κάνει 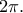 Τις πράξεις θα τις γράψω το απόγευμα γιατί πρέπει να φύγω για δουλειά.
Τις πράξεις θα τις γράψω το απόγευμα γιατί πρέπει να φύγω για δουλειά.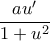 για
για  και κάποια συνάρτηση
και κάποια συνάρτηση  με
με 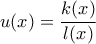 και έπειτα από πράξεις η ολοκληρωτέα
και έπειτα από πράξεις η ολοκληρωτέα 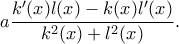 Ξεκινάμε από τον παρονομαστή μήπως καταφέρουμε να τον γράψουμε σαν
Ξεκινάμε από τον παρονομαστή μήπως καταφέρουμε να τον γράψουμε σαν 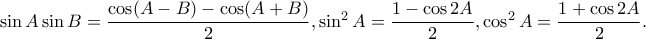
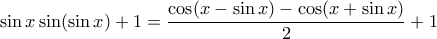
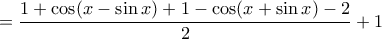
 .
.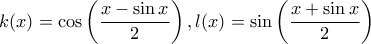 και τότε
και τότε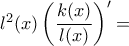
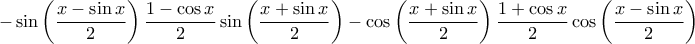
![= \dfrac{\cos x }{2} \left [\sin \left ( \dfrac{x-\sin x}{2} \right ) \sin \left ( \dfrac{x+\sin x}{2} \right )-\cos \left ( \dfrac{x-\sin x}{2} \right ) \cos \left ( \dfrac{x+\sin x}{2} \right ) \right ] = \dfrac{\cos x }{2} \left [\sin \left ( \dfrac{x-\sin x}{2} \right ) \sin \left ( \dfrac{x+\sin x}{2} \right )-\cos \left ( \dfrac{x-\sin x}{2} \right ) \cos \left ( \dfrac{x+\sin x}{2} \right ) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/421b732337d3b479e3b8abc500ed2811.png)
![-\dfrac{1}{2}\left [\sin \left ( \dfrac{x-\sin x}{2} \right ) \sin \left ( \dfrac{x+\sin x}{2} \right ) +\cos \left ( \dfrac{x-\sin x}{2} \right ) \cos \left ( \dfrac{x+\sin x}{2} \right ) \right ]. -\dfrac{1}{2}\left [\sin \left ( \dfrac{x-\sin x}{2} \right ) \sin \left ( \dfrac{x+\sin x}{2} \right ) +\cos \left ( \dfrac{x-\sin x}{2} \right ) \cos \left ( \dfrac{x+\sin x}{2} \right ) \right ].](/forum/ext/geomar/texintegr/latexrender/pictures/256947627e538a00d8ea97143998e1a5.png)
![=-\dfrac{1}{2}\left (\cos x \left [ \cos x \right ]+\left [\cos(\sin x) \right ] \right )=-\dfrac{1}{2}\left ( \cos^2x +\cos(\sin x)\right ). =-\dfrac{1}{2}\left (\cos x \left [ \cos x \right ]+\left [\cos(\sin x) \right ] \right )=-\dfrac{1}{2}\left ( \cos^2x +\cos(\sin x)\right ).](/forum/ext/geomar/texintegr/latexrender/pictures/77b69ad8f94ebd5e1f775c019b9d82ec.png)
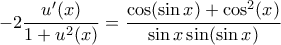 με
με 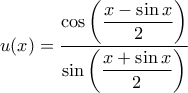
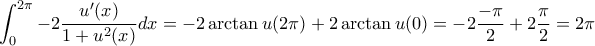
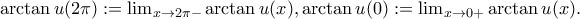
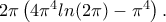
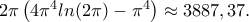 Από την άλλη, βάζοντας τιμές στο
Από την άλλη, βάζοντας τιμές στο  όπως
όπως 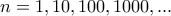
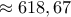 τιμή αρκετά
τιμή αρκετά  δεν είναι καθόλου τυχαία τιμή στην οποία φρακάρει το WOLPHRAM. Είναι προσεγγιστική τιμή του
δεν είναι καθόλου τυχαία τιμή στην οποία φρακάρει το WOLPHRAM. Είναι προσεγγιστική τιμή του 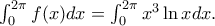


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες