Θέματα της δεύτερης μέρας για την 10η τάξη.
1. Δίνεται ένα ευθύγραμμο μονοπάτι, που αποτελείται από πράσινες και κόκκινες σανίδες (μονοπάτι ευθύγραμμο τμήμα, διαμερισμένο σε σανίδες ευθύγραμμα τμήματα). Τα χρώματα των σανίδων εναλλάσσονται: η πρώτη και η τελευταία σανίδα είναι πράσινες. Είναι γνωστό ότι τα μήκη όλων των σανίδων είναι μεγαλύτερα του εκατοστού και μικρότερα του μέτρου, καθώς και ότι το μήκος κάθε επόμενης σανίδας είναι μεγαλύτερο της προηγούμενης. Ένας τζιτζίκι θέλει να μεταπηδήσει προς τα εμπρός κατά μήκος του μονοπατιού σε αυτές τις σανίδες, πατώντας σε κάθε πράσινη σανίδα τουλάχιστον μια φορά και μη πατώντας σε καμία κόκκινη (ή το όριο μεταξύ διαδοχικών σανίδων). Να αποδείξετε, ότι το τζιτζίκι μπορεί να το καταφέρει αυτό έτσι, ώστε μεταξύ των μηκών των αλμάτων του να συναντώνται το πολύ
 διαφορετικές τιμές. (Τ. Κοροτσένκο)
διαφορετικές τιμές. (Τ. Κοροτσένκο)2. Δίνεται ένα παραλληλόγραμμο
 . Το σημείο
. Το σημείο  είναι το μέσο του τόξου
είναι το μέσο του τόξου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  . Στο τμήμα
. Στο τμήμα  δίνεται σημείο
δίνεται σημείο  και στο τμήμα
και στο τμήμα  σημείο
σημείο  . Είναι γνωστό ότι
. Είναι γνωστό ότι  . Να αποδείξετε, ότι τα σημεία
. Να αποδείξετε, ότι τα σημεία  και
και  είναι ομοκυκλικά. (Α. Τεριέσιν)
είναι ομοκυκλικά. (Α. Τεριέσιν)3. Έστω ότι δίνονται δυο φυσικοί (μη μηδενικοί) αριθμοί
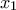 και
και  . Σε μια ευθεία δίνονται
. Σε μια ευθεία δίνονται  λευκά και
λευκά και  μαύρα τμήματα, εξάλλου
μαύρα τμήματα, εξάλλου  και
και  . Είναι γνωστό, ότι κανένα ζεύγος τμημάτων ίδιου χρώματος δεν τέμνονται (ούτε έχουν κοινά άκρα). Επίσης είναι γνωστό, ότι για οποιαδήποτε επιλογή
. Είναι γνωστό, ότι κανένα ζεύγος τμημάτων ίδιου χρώματος δεν τέμνονται (ούτε έχουν κοινά άκρα). Επίσης είναι γνωστό, ότι για οποιαδήποτε επιλογή 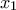 λευκών τμημάτων και
λευκών τμημάτων και  μαύρων τμημάτων οπωσδήποτε κάποιο ζεύγος επιλεγμένων τμημάτων θα τέμνεται. Να αποδείξετε ότι
μαύρων τμημάτων οπωσδήποτε κάποιο ζεύγος επιλεγμένων τμημάτων θα τέμνεται. Να αποδείξετε ότι  .
. (Γκ. Τσελνόκοβ)
4. Δίνεται ένας φυσικός αριθμός
 . Η Άννα γράφει σε κύκλο
. Η Άννα γράφει σε κύκλο  φυσικούς αριθμούς (μη μηδενικούς). Στην συνέχεια η Αθηνά κάνει την εξής πράξη: μεταξύ οποιονδήποτε δυο γειτονικών αριθμών
φυσικούς αριθμούς (μη μηδενικούς). Στην συνέχεια η Αθηνά κάνει την εξής πράξη: μεταξύ οποιονδήποτε δυο γειτονικών αριθμών  και
και  γράφει κάποιον διαιρέτη του αριθμού
γράφει κάποιον διαιρέτη του αριθμού  , μεγαλύτερου του
, μεγαλύτερου του  . Ύστερα η Αθηνά σβήνει τους αρχικούς αριθμούς και αποκτά μια νέα συλλογή
. Ύστερα η Αθηνά σβήνει τους αρχικούς αριθμούς και αποκτά μια νέα συλλογή  αριθμών, που βρίσκονται σε κύκλο. Μπορεί άραγε πάντα η Αθηνά να κάνει πράξεις με τέτοιο τρόπο, ώστε μετά από κάμποσες πράξεις όλοι οι αριθμοί να προκύψουν ίσοι μεταξύ τους; (Τ. Κοροτσένκο)
αριθμών, που βρίσκονται σε κύκλο. Μπορεί άραγε πάντα η Αθηνά να κάνει πράξεις με τέτοιο τρόπο, ώστε μετά από κάμποσες πράξεις όλοι οι αριθμοί να προκύψουν ίσοι μεταξύ τους; (Τ. Κοροτσένκο)