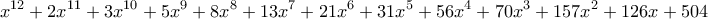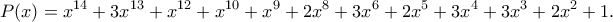polysot έγραψε:Αν κάποιος πρόλαβε και κατέβασε τα αποτελέσματα του Αρχιμήδη από τη σελίδα της ΕΜΕ πριν πέσει, ας τα βάλει εδώ να τα δούμε κι εμείς...
Αρχιμήδης 2017
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
Re: Αρχιμήδης 2017
- Συνημμένα
-
- Screenshot (29).png (244.83 KiB) Προβλήθηκε 2467 φορές
Ανδρέας Χαραλαμπόπουλος
Λέξεις Κλειδιά:
Re: Αρχιμήδης 2017
- Συνημμένα
-
- hms.gr-Αποτελέσματα διαγωνισμού Αρχιμήδη 2017 Ελληνική Μαθηματική Εταιρεία.pdf
- (36.16 KiB) Μεταφορτώθηκε 198 φορές
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: Αρχιμήδης 2017
Ξέρει κάποιος πόσο ειναι η βάση στα μικρά;polysot έγραψε:Αν κάποιος πρόλαβε και κατέβασε τα αποτελέσματα του Αρχιμήδη από τη σελίδα της ΕΜΕ πριν πέσει, ας τα βάλει εδώ να τα δούμε κι εμείς...
Re: Αρχιμήδης 2017
Μονο αυτά τα παιδια που θα βραβευτουν αύριο συνεχίζουν;sofiaxen έγραψε:Ξέρει κάποιος πόσο ειναι η βάση στα μικρά;polysot έγραψε:Αν κάποιος πρόλαβε και κατέβασε τα αποτελέσματα του Αρχιμήδη από τη σελίδα της ΕΜΕ πριν πέσει, ας τα βάλει εδώ να τα δούμε κι εμείς...
Re: Αρχιμήδης 2017
Για το δεύτερο θέμα των μικρών
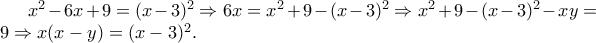 .
.
Απο την οποία πρέπει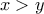 δηλαδή
δηλαδή 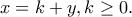 Συμμετρικά για τις άλλες εξισώσεις ισχύουν
Συμμετρικά για τις άλλες εξισώσεις ισχύουν 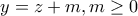 και
και 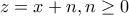 . Με αντικατάσταση έχουμε:
. Με αντικατάσταση έχουμε: 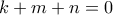 άρα
άρα 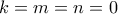 δηλαδή
δηλαδή 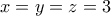
επεξεργασία: Καταλάθος έγραψα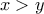 ενώ ήθελα να γράψω
ενώ ήθελα να γράψω 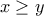 .
.
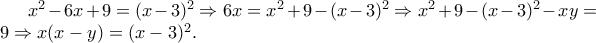 .
. Απο την οποία πρέπει
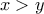 δηλαδή
δηλαδή 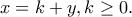 Συμμετρικά για τις άλλες εξισώσεις ισχύουν
Συμμετρικά για τις άλλες εξισώσεις ισχύουν 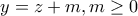 και
και 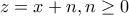 . Με αντικατάσταση έχουμε:
. Με αντικατάσταση έχουμε: 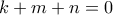 άρα
άρα 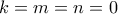 δηλαδή
δηλαδή 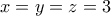
επεξεργασία: Καταλάθος έγραψα
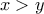 ενώ ήθελα να γράψω
ενώ ήθελα να γράψω 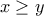 .
.
τελευταία επεξεργασία από HerrGauss σε Σάβ Μαρ 04, 2017 10:43 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
ΤΣΟΠΕΛΑΣ ΓΙΑΝΝΗΣ
- Δημοσιεύσεις: 298
- Εγγραφή: Σάβ Απρ 03, 2010 5:06 pm
- Τοποθεσία: Αμαλιάδα - Ηλείας
Re: Αρχιμήδης 2017
Συγχαρητήρια σε όλους τους μαθητές που διακρίθηκαν και ιδιαίτερα στους Ηλείους μαθητές Aδαμοπουλο Διονύση και Αδαμόπουλο Δημήτρη!!
Re: Αρχιμήδης 2017
Συγχαρητήρια Σε Όλους Τους Επιτυχόντες Και Μη Και Καλή Επιτυχία Στον Προκριματικό!
Bye :')
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13301
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Αρχιμήδης 2017
Συγχαρητήρια σε όλους τους επιτυχόντες!
Ειδικότερα στους "δικούς μας" Ορέστη Λιγνό, Διονύση Αδαμόπουλο, Ραφαήλ Ψυρούκη και Γιάννη Σημαντήρη απ' τη Γλυφάδα!
Ειδικότερα στους "δικούς μας" Ορέστη Λιγνό, Διονύση Αδαμόπουλο, Ραφαήλ Ψυρούκη και Γιάννη Σημαντήρη απ' τη Γλυφάδα!
-
christodoulos703
- Δημοσιεύσεις: 72
- Εγγραφή: Τετ Αύγ 03, 2016 1:57 pm
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13301
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Αρχιμήδης 2017
Συγχαρητήρια και σε σένα, καθώς επίσης και σε άλλα παιδιά τουchristodoulos703 έγραψε:Και εγώστο παρά πέντε.
Τέλος τα Θερμά μου Συγχαρητήρια σε όλα τα παιδιά που συμμετείχαν στον διαγωνισμό!
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Αρχιμήδης 2017
Συγχαρητήρια σε όλα τα παιδιά που διακρίθηκαν. Είναι μεγάλη επιτυχία , άθλος θα έλεγα !
Σχεδιάζουμε να κατέβουμε στην απονομή και τα συγχαρούμε και από κοντά !!!
Μπ
Σχεδιάζουμε να κατέβουμε στην απονομή και τα συγχαρούμε και από κοντά !!!
Μπ
Re: Αρχιμήδης 2017
Κάποιες σκέψεις πάνω στο 4ο ΘΕΜΑ μετά την πολύ ωραία λύση του Νίκου.achilleas έγραψε: ....
Σημείωση: Το πολυώνυμοπου προκύπτει από τη λύση του Νίκου είναι το
κι άρα
...
Ένας brute force τρόπος να βρούμε το παραπάνω πολυώνυμο είναι να ξεκινήσουμε με το
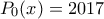 .
.Παρατηρούμε ότι για να "ρίξουμε" την τιμή του
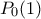 αρκεί να προσθέσουμε πολυώνυμο
αρκεί να προσθέσουμε πολυώνυμο 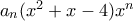 για κατάλληλα
για κατάλληλα  και
και 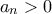 , αφού για
, αφού για  το τελευταίο δίνει τιμή
το τελευταίο δίνει τιμή 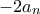 .
.Δηλαδή, αφαιρούμε ένα θετικό άρτιο ακέραιο κάθε φορά. Κρατάμε τους συντελεστές μη αρνητικούς και η τιμή του νέου πολυωνύμου στο
 είναι μικρότερη από την προηγούμενη.
είναι μικρότερη από την προηγούμενη.Σε κάθε βήμα, από το
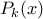 βαθμού
βαθμού  παίρνουμε ένα πολυώνυμο
παίρνουμε ένα πολυώνυμο 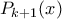 βαθμού
βαθμού  , με
, με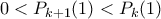 .
.Έτσι παίρνουμε μια φθίνουσα ακολουθία θετικών ακεραίων, η οποία αναγκαστικά θα τερματίσει.
Ξεκινώντας, αφού
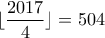 , παίρνουμε
, παίρνουμε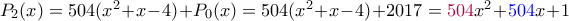 με
με 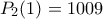 .
.Aφού
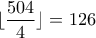 , θέτουμε
, θέτουμε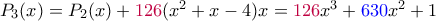 με
με 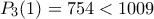 .
.Κάθε φορά, κοιτάμε τον πρώτο συντελεστή από τα δεξιά που είναι μεγαλύτερος ή ίσος του 4, και προσθέτουμε κατάλληλο πολλαπλάσιο του
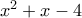 .
.Aφού
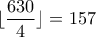 , θέτουμε
, θέτουμε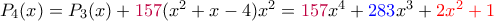 με
με 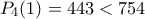 .
.Aφού
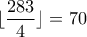 , θέτουμε
, θέτουμε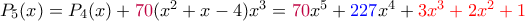 με
με 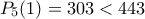 .
.Συνεχίζοντας με τον ίδιο τρόπο, κοιτάμε κάθε φορά τον μπλε συντελεστή και παίρνουμε τα παρακάτω- η "ουρά" είναι με κόκκινο και παραμένει η ίδια-

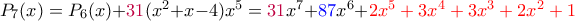
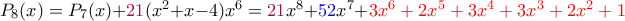
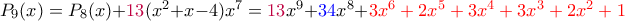
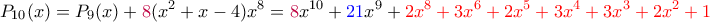
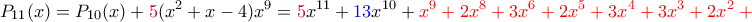
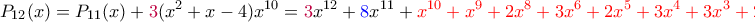
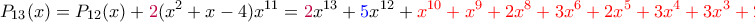
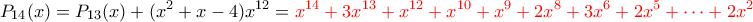
Οι συνετελεστές του τελευταίου είναι όλοι μη αρνητικοί και μικρότεροι του 4, οπότε η παραπάνω διαδικασία τερματίζει.
Αν παρατηρήσουμε την αντιστοιχία των μωβ συντελεστών, οι υπολογισμοί γίνονται ευκολότερα απ'ότι δείχνουν.
Προσθήκη: Τα παραπάνω παρουσιάζονται απλούστερα στο αμέσως επόμενο μήνυμα.
Φιλικά,
Αχιλλέας
τελευταία επεξεργασία από achilleas σε Κυρ Μαρ 05, 2017 6:31 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Re: Αρχιμήδης 2017
Σε συνέχεια του παραπάνω, θα μπορούσαμε να απλοποιήσουμε την γραφή και να την γράψουμε πιο κομψά, εστιάζοντας μόνο στην ακολουθία των συντελεστών κάθε φορά, γράφοντας την "ανάποδα" αυτή τη φορά:achilleas έγραψε: ....
Οι συνετελεστές του τελευταίου είναι όλοι μη αρνητικοί και μικρότεροι του 4, οπότε η παραπάνω διαδικασία τερματίζει.
Αν παρατηρήσουμε την αντιστοιχία των μωβ συντελεστών, οι υπολογισμοί γίνονται ευκολότερα απ'ότι δείχνουν.
(1,504,504)
(1,0,630,126)
(1,0,2,283,157) --> π.χ. 2 =υπόλοιπο διαίρεσης
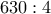 ,
, 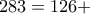 πηλίκο της
πηλίκο της 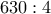 , 157=πηλίκο της
, 157=πηλίκο της 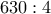
(1,0,2,3,227,70)
(1,0,2,3,3,126,56)
(1,0,2,3,3,2,87,31)
(1,0,2,3,3,2,3,52,21)--> π.χ. 3 =υπόλοιπο διαίρεσης
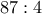 ,
, 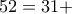 πηλίκο της
πηλίκο της 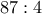 , και 21=πηλίκο της
, και 21=πηλίκο της 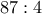
(1,0,2,3,3,2,3,0,34,13)
(1,0,2,3,3,2,3,0,2,21,8)
(1,0,2,3,3,2,3,0,2,1,13,5)
(1,0,2,3,3,2,3,0,2,1,1,8,3)
(1,0,2,3,3,2,3,0,2,1,1,0,5,2)
(1,0,2,3,3,2,3,0,2,1,1,0,1,3,1)
Σε κάθε βήμα ουσιαστικά "απλά" εφαρμόζουμε την Ευκλείδεια διαίρεση
Done!
Φιλικά,
Αχιλλέας
-
Κατερινόπουλος Νικόλας
- Δημοσιεύσεις: 659
- Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm
- Τοποθεσία: Καλαμάτα, Μεσσηνία
Re: Αρχιμήδης 2017
Καλησπέρα μέλη του Mathematica, είμαι ο Κατερινόπουλος Νικόλας, μαθητής της έκτης Δημοτικού και είμαι καινούριο μέλος!!!
-
Κατερινόπουλος Νικόλας
- Δημοσιεύσεις: 659
- Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm
- Τοποθεσία: Καλαμάτα, Μεσσηνία
Re: Αρχιμήδης 2017
Καλησπέρα σας!
Θερμά Συγχαρητήρια σε όλους τους διακριθέντες του χθεσινού διαγωνισμού, αλλά και σε όλους όσους διαγωνίσθηκαν!
Και τώρα τι;
Όσοι διακρίθηκαν θα συνεχίσουν την προετοιμασία τους φυσικά.
Το ίδιο, όμως, πρέπει να ισχύσει για όλους!
Η ενασχόληση με τα μαθηματικά και την επίλυση προβλημάτων είναι μια υπέροχη διανοητική διαδικασία!
Δεν πρέπει να περιορίζεται λίγο πριν την περίοδο διαγωνισμών! Πρέπει να είναι συνεχής!
Δεν έχει να κάνει με "βάσεις πρόκρισης", αλλά με την αναζήτηση λύσης, την εύρεση της, και μετά την επινόηση ακόμα μιας, ίσως κομψότερης, μέχρι να μας σαγηνεύσει ένα άλλο πρόβλημα και να συνεχίσουμε προς άλλες οδούς.
Καλή συνέχεια σε όλους τους μαθητές που αγαπούν τα μαθηματικά με την επίλυση προβλημάτων!
Θαυμάζουμε τις επιτυχίες σας και απολαμβάνουμε τις λύσεις σας! Έχετε πολλά να δώσετε! Προσμένουμε πολλά από εσάς!
Φιλικά,
Αχιλλέας
Θερμά Συγχαρητήρια σε όλους τους διακριθέντες του χθεσινού διαγωνισμού, αλλά και σε όλους όσους διαγωνίσθηκαν!
Και τώρα τι;
Όσοι διακρίθηκαν θα συνεχίσουν την προετοιμασία τους φυσικά.
Το ίδιο, όμως, πρέπει να ισχύσει για όλους!
Η ενασχόληση με τα μαθηματικά και την επίλυση προβλημάτων είναι μια υπέροχη διανοητική διαδικασία!
Δεν πρέπει να περιορίζεται λίγο πριν την περίοδο διαγωνισμών! Πρέπει να είναι συνεχής!
Δεν έχει να κάνει με "βάσεις πρόκρισης", αλλά με την αναζήτηση λύσης, την εύρεση της, και μετά την επινόηση ακόμα μιας, ίσως κομψότερης, μέχρι να μας σαγηνεύσει ένα άλλο πρόβλημα και να συνεχίσουμε προς άλλες οδούς.
Καλή συνέχεια σε όλους τους μαθητές που αγαπούν τα μαθηματικά με την επίλυση προβλημάτων!
Θαυμάζουμε τις επιτυχίες σας και απολαμβάνουμε τις λύσεις σας! Έχετε πολλά να δώσετε! Προσμένουμε πολλά από εσάς!
Φιλικά,
Αχιλλέας
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες