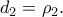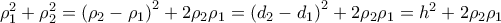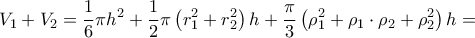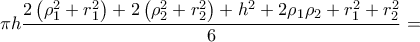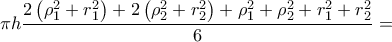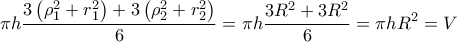2. Έστω 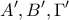 τα ίχνη των υψών τριγώνου
τα ίχνη των υψών τριγώνου  .
.
α) Να δειχτεί οτι αν η περίμετρος του τριγώνου 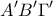 ισούται με την διάμετρο του περιγεγραμμένου κύκλου του
ισούται με την διάμετρο του περιγεγραμμένου κύκλου του  ,
,
τότε θα ισχύει οτι 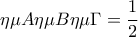
β) Να βρεθούν οι πλευρές και οι γωνίες του τριγώνου 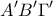 και η ακτίνα του περιγεγραμμένου κύκλου του
και η ακτίνα του περιγεγραμμένου κύκλου του
συναρτήσει των γωνιών του  και της ακτίνας του περιγεγραμμένου κύκλου του
και της ακτίνας του περιγεγραμμένου κύκλου του  .
Το πρώτο σκέλος του θέματος ισχύει μόνο στα οξυγώνια τρίγωνα
.
Το πρώτο σκέλος του θέματος ισχύει μόνο στα οξυγώνια τρίγωνα. Το τι ισχύει στα αμβλυγώνια θα το δούμε σε αυτήν τη δημοσίευση. Είναι μια καλή ευκαιρία να γραφούν κάποια βασικά για τα
ορθικά τρίγωνα. Στη διαπραγμάτευση του θέματος θα είμαι σύντομος εκεί που χρειάζεται, αναλυτικός εκεί που πρέπει.
α)Από το εγγράψιμο τετράπλευρο
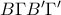
προκύπτει ότι τα τρίγωνα
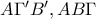
είναι όμοια.
Έτσι
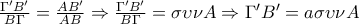
.
Με αντίστοιχες σκέψεις μπορώ να γράψω ότι :
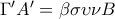
και
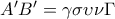
.
Άρα η περίμετρος του
ορθικού τριγώνου 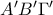
του τριγώνου

είναι ίση με
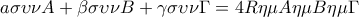
.
Φυσικά η τελευταία ισότητα θα αποδειχθεί αναλυτικά αμέσως πιο κάτω.
Πρώτα θα αποδειχθεί ότι
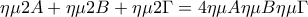
.
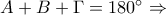
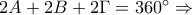
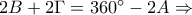
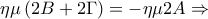
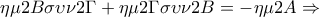
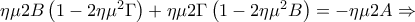
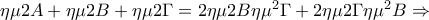
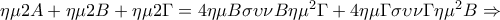
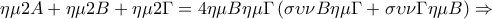
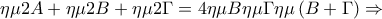
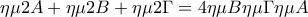
Έτσι
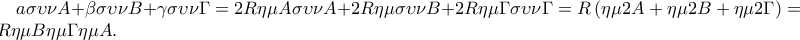
Το ζητούμενο στο 1ο ερώτημα είναι πλέον εμφανές. Τονίζω ότι η παραπάνω διαπραγμάτευση έχει να κάνει μόνο με οξυγώνια τρίγωνα.
Θα δούμε τώρα τι γίνεται αν το τρίγωνο

είναι αμβλυγώνιο με
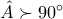
.
Από την ομοιότητα των τριγώνων
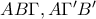
προκύπτει ότι
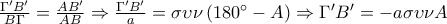
Για να μη γράφω πολλά , με αντίστοιχες σκέψεις ισχύει ότι
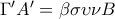
και
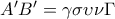
.
Έτσι η περίμετρος του ορθικού τριγώνου του τριγώνου

είναι ίση με
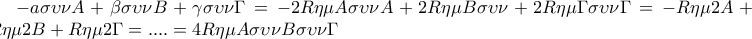
.
Το γεγονός ότι
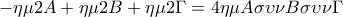
νομίζω ότι μπορεί να το αποδείξει κάποιος με σκέψεις σαν κι αυτές που έγραψα λίγο πιο πάνω , σίγουρα καταλαβαίνετε τι εννοώ.
Ανάλογες διατυπώσεις προκύπτουν όταν
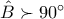
ή όταν
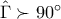
.
β)Ας ξεκινήσουμε με τα οξυγώνια τρίγωνα.
Από το εγγράψιμο τετράπλευρο
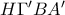
προκύπτει ότι
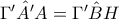
.
Από το εγγράψιμο τετράπλευρο
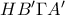
προκύπτει ότι
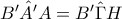
.
Όμως από το εγγράψιμο τετράπλευρο
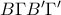
προκύπτει ότι
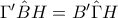
.
Συνεπώς
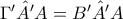
.
Συνεπώς
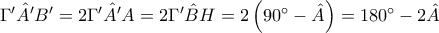
.
Με ανάλογο τρόπο βρίσκεται ότι
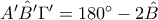
,
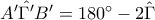
.
Ας ασχοληθούμε τώρα με την ακτίνα
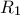
του περιγεγραμμένου κύκλου του ορθικού τριγώνου οξυγωνίου τριγώνου.
Θα βρεθεί με το νόμο του ημιτόνου.
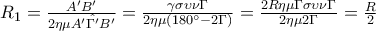
.
Ας δούμε σύντομα τι γίνεται όταν στο τρίγωνο

ισχύει
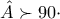
.
Δεν είναι πλέον δύσκολο να αποδειχθεί ότι η

διχοτομεί τη
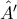
, η
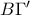
διχοτομεί τη
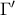
και ότι
η
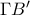
διχοτομεί τη
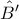
,
αναφέρομαι στις γωνίες του ορθικού τριγώνου.
![\hat{A'}=2B'\hat{A'}A=2B'\hat{B}A=2\left[ 90^{\circ}-\left(180^{\circ}-A \right) \right]=2A-180^{\circ} \hat{A'}=2B'\hat{A'}A=2B'\hat{B}A=2\left[ 90^{\circ}-\left(180^{\circ}-A \right) \right]=2A-180^{\circ}](/forum/ext/geomar/texintegr/latexrender/pictures/3533c2e1f1ffcb57dc8702255bf696e0.png)
Με χρήση των κατάλληλων εγραψίμων τετραπλέυρων βρίσκεται ότι
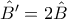
και ότι
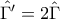
.
Το αξιοσημείωτο είναι ότι δεν αλλάζει το μήκος του περιγεγραμμένου κύκλου του ορθικού τριγώνου.
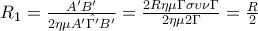
Τώρα θα μου πείτε , γιατί δε γράφω ότι ο περιγεγραμμένος κύκλος του ορθικού τριγώνου είναι ο κύκλος Euler του τριγώνου

ο οποίος έχει ακτίνα ίση με
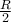
. Δεν θέλω να επικαλεστώ αμέσως γνώσεις που τα παιδιά δε διδάσκονται στο σχολείο. Ίσως το σχολικό έτος 1937-1938 τα πράγματα να ΄ταν αλλιώς , δεν ξέρω....
Αναρωτιέμαι πόσοι θα 'χουν την υπομονή να διαβάσουν τα όσα έγραψα....
Πάντως σε κάποιους θα φανούν χρήσιμα.
Η παρούσα διαπραγμάτευση θα μπορούσε να εξετάσει τι γίνεται με το εμβαδόν του ορθικού τριγώνου ή με το μήκος της ακτίνας του εγγεγραμμένου τού κύκλου. Αυτό θα το αφήσω για άλλη στιγμή....
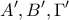 τα ίχνη των υψών τριγώνου
τα ίχνη των υψών τριγώνου  .
.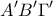 ισούται με την διάμετρο του περιγεγραμμένου κύκλου του
ισούται με την διάμετρο του περιγεγραμμένου κύκλου του  ,
, 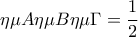
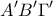 και η ακτίνα του περιγεγραμμένου κύκλου του
και η ακτίνα του περιγεγραμμένου κύκλου του  . και της ακτίνας του περιγεγραμμένου κύκλου του
. και της ακτίνας του περιγεγραμμένου κύκλου του  .
.
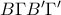 προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα 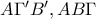 είναι όμοια.
είναι όμοια.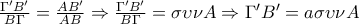 .
.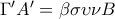 και
και 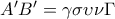 .
.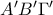 του τριγώνου
του τριγώνου  είναι ίση με
είναι ίση με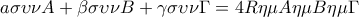 .
.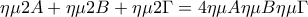 .
.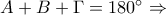
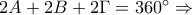
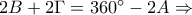
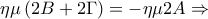
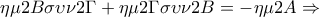
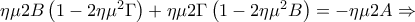
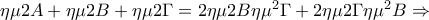
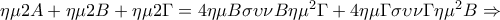
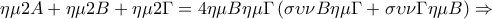
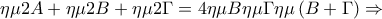
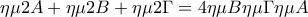
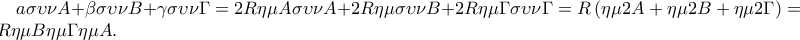
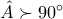 .
.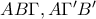 προκύπτει ότι
προκύπτει ότι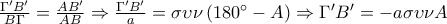
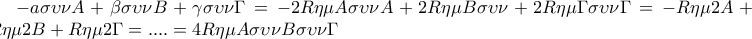 .
.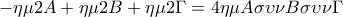 νομίζω ότι μπορεί να το αποδείξει κάποιος με σκέψεις σαν κι αυτές που έγραψα λίγο πιο πάνω , σίγουρα καταλαβαίνετε τι εννοώ.
νομίζω ότι μπορεί να το αποδείξει κάποιος με σκέψεις σαν κι αυτές που έγραψα λίγο πιο πάνω , σίγουρα καταλαβαίνετε τι εννοώ.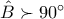 ή όταν
ή όταν 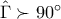 .
.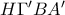 προκύπτει ότι
προκύπτει ότι 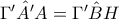 .
.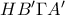 προκύπτει ότι
προκύπτει ότι 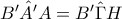 .
.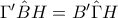 .
.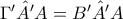 .
.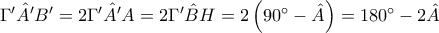 .
.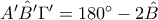 ,
, 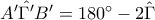 .
.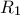 του περιγεγραμμένου κύκλου του ορθικού τριγώνου οξυγωνίου τριγώνου.
του περιγεγραμμένου κύκλου του ορθικού τριγώνου οξυγωνίου τριγώνου.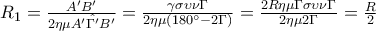 .
. ισχύει
ισχύει 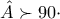 .
. διχοτομεί τη
διχοτομεί τη 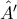 , η
, η 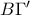 διχοτομεί τη
διχοτομεί τη 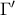 και ότι
και ότι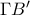 διχοτομεί τη
διχοτομεί τη 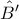 ,
, ![\hat{A'}=2B'\hat{A'}A=2B'\hat{B}A=2\left[ 90^{\circ}-\left(180^{\circ}-A \right) \right]=2A-180^{\circ} \hat{A'}=2B'\hat{A'}A=2B'\hat{B}A=2\left[ 90^{\circ}-\left(180^{\circ}-A \right) \right]=2A-180^{\circ}](/forum/ext/geomar/texintegr/latexrender/pictures/3533c2e1f1ffcb57dc8702255bf696e0.png)
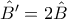 και ότι
και ότι 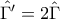 .
.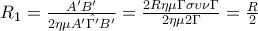
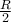 . Δεν θέλω να επικαλεστώ αμέσως γνώσεις που τα παιδιά δε διδάσκονται στο σχολείο. Ίσως το σχολικό έτος 1937-1938 τα πράγματα να ΄ταν αλλιώς , δεν ξέρω....
. Δεν θέλω να επικαλεστώ αμέσως γνώσεις που τα παιδιά δε διδάσκονται στο σχολείο. Ίσως το σχολικό έτος 1937-1938 τα πράγματα να ΄ταν αλλιώς , δεν ξέρω.... η ακτίνα των βάσεων του κυλίνδρου που είναι και η ακτίνα της εγγεγραμμένης στον κύλινδρο σφαίρας .
η ακτίνα των βάσεων του κυλίνδρου που είναι και η ακτίνα της εγγεγραμμένης στον κύλινδρο σφαίρας . η απόσταση του κέντρου της σφαίρας από το επίπεδο που τέμνει τη σφαίρα, τον κύλινδρο και τον κώνο και είναι
η απόσταση του κέντρου της σφαίρας από το επίπεδο που τέμνει τη σφαίρα, τον κύλινδρο και τον κώνο και είναι  και τον κώνο κατά
και τον κώνο κατά 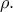
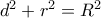

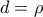 και έτσι
και έτσι 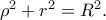
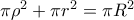 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.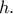 O όγκος του κυλίνδρου αυτού είναι ίσος με
O όγκος του κυλίνδρου αυτού είναι ίσος με 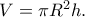
 την ακτίνα της μικρής βάσης του και
την ακτίνα της μικρής βάσης του και 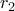 την ακτίνα της
την ακτίνα της 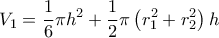
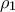 την ακτίνα της μικρής βάσης του και
την ακτίνα της μικρής βάσης του και 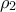 την ακτίνα της μεγάλης βάσης του.
την ακτίνα της μεγάλης βάσης του.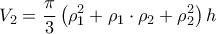
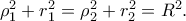
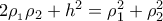
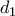 η απόσταση του κέντρου της σφαίρας από το ένα επίπεδο και
η απόσταση του κέντρου της σφαίρας από το ένα επίπεδο και 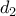 η απόσταση του
η απόσταση του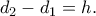
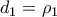 και
και