Καλό για Γ λυκείου! Θα το δώσω σε μαθητή δίνοντας και την πηγή του

. Επειδή μου άρεσε σαν θέμα, βάζω τη λύση μου.
1. Έχουμε
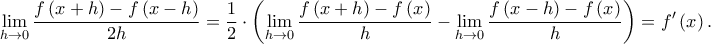 2.
2. Η

είναι συνεχής στο
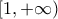
και παραγωγίσιμη στο
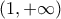
με
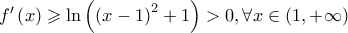
, άρα η

είναι γνησίως αύξουσα στο
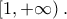
Η

είναι συνεχής και γνησίως αύξουσα στο
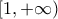
, άρα
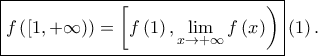
Για κάθε

η

είναι συνεχής στο
![\left [ 1,x \right ] \left [ 1,x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/560dcdf3db182a4e796d9c084358929c.png)
και παραγωγίσιμη στο
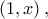
άρα από ΘΜΤ υπάρχει
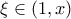
με
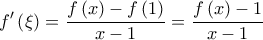
και αφού
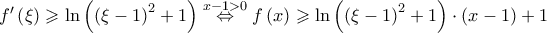
και επειδή
![\displaystyle \lim_{x\rightarrow +\infty}\left [ \ln\left ( \left ( \xi -1 \right )^{2}+1 \right )\cdot \left ( x-1 \right )+1 \right ]=+\infty, \displaystyle \lim_{x\rightarrow +\infty}\left [ \ln\left ( \left ( \xi -1 \right )^{2}+1 \right )\cdot \left ( x-1 \right )+1 \right ]=+\infty,](/forum/ext/geomar/texintegr/latexrender/pictures/fa1f593cc4590045930ad251837ebdde.png)
άρα
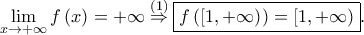 3.
3. Θεωρούμε την συνάρτηση
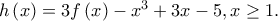
Είναι
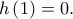
Έστω ότι η

έχει κάποια ρίζα

Η

είναι συνεχής στο
![\left [ 1,\rho \right ] \left [ 1,\rho \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/fc66e7bdf92aade6de829530c1a5cc55.png)
και παραγωγίσιμη στο
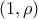
με
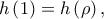
άρα από Θ. Rolle υπάρχει
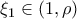
με
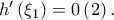
Η

είναι παραγωγίσιμη στο
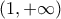
με
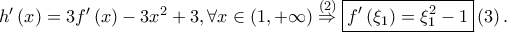
Συνεπώς
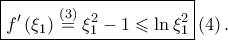
Θεωρούμε την συνάρτηση
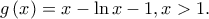
Η

είναι παραγωγίσιμη με
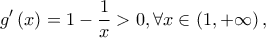
άρα η

είναι γνησίως αύξουσα στο
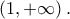
Η

είναι συνεχής και γνησίως αύξουσα στο
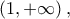
άρα
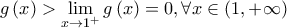
και από την σχέση
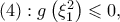
άτοπο. Άρα, η εξίσωση έχει μοναδική λύση στο
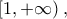
την
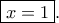 4.i)
4.i) Για κάθε
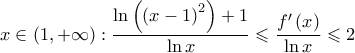
και αφού
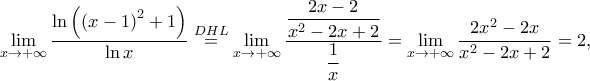
άρα από το Κριτήριο Παρεμβολής
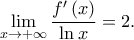
Είναι
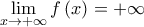
και
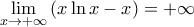
και αφού το όριο
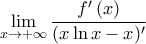
υπάρχει και ισούται με
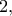
από τον κανόνα De L' Hospital και το όριο
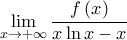
υπάρχει και είναι
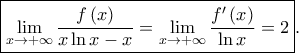 ii)
ii) Αφού
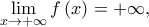
η

δεν έχει οριζόντια ασύμπτωτη στο
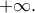
Για κάθε
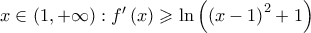
και αφού
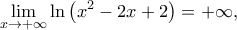
άρα
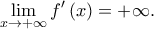
Αφού
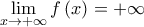
και το όριο

υπάρχει και ισούται με
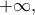
από τον Κανόνα De L' Hospital (το όριο
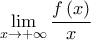
είναι απροσδιόριστη μορφή
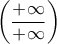
) και το όριο
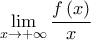
υπάρχει και είναι
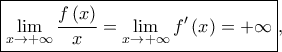
άρα η

δεν έχει πλάγια ασύμπτωτη στο
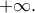 5.
5. Έστω ότι υπάρχει
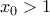
με
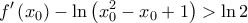
. Αφού
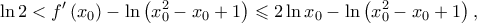
άρα
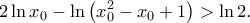
Θεωρούμε την συνάρτηση

Η

είναι παραγωγίσιμη με
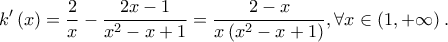
Είναι:
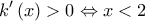
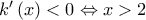
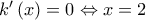
Άρα, η

είναι γνησίως αύξουσα στο
![\left ( 1,2 \right ] \left ( 1,2 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e600b6010271879fe15c690839d810fd.png)
και γνησίως φθίνουσα στο
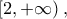
άρα
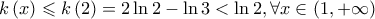
και
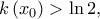
άτοπο.
Έστω ότι υπάρχει
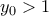
με
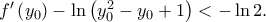
Αφού
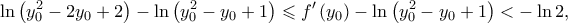
άρα

Θεωρούμε την συνάρτηση
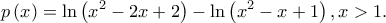
Η

είναι παραγωγίσιμη με
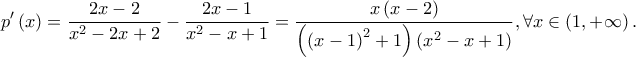
Είναι:
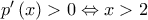
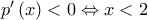
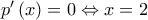
Άρα, η

είναι γνησίως φθίνουσα στο
![\left ( 1,2 \right ] \left ( 1,2 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e600b6010271879fe15c690839d810fd.png)
και γνησίως αύξουσα στο
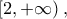
άρα
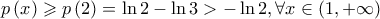
και
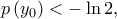
άτοπο.
Επομένως
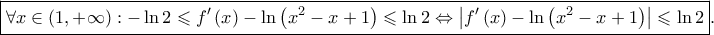
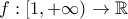 για την οποία ισχύουν τα παρακάτω:
για την οποία ισχύουν τα παρακάτω: και παραγωγίσιμη στο
και παραγωγίσιμη στο 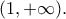
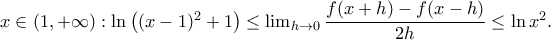

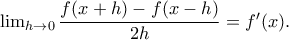
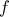 είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.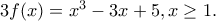
 είναι το
είναι το 
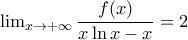 .
.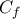 δεν έχει ασύμπτωτη στο
δεν έχει ασύμπτωτη στο  .
. ισχύει:
ισχύει: 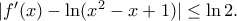

![\underset{h\to 0}{\mathop{\lim }}\,\frac{f(x+h)-f(x-h)}{2h}=\underset{h\to 0}{\mathop{\frac{1}{2}\lim }}\,\left( \frac{f(x+h)-f(x)}{h}+\frac{f(x-h)-f(x)}{-h} \right)=\frac{1}{2}\left[ {f}'(x)+{f}'(x) \right]={f}'(x) \underset{h\to 0}{\mathop{\lim }}\,\frac{f(x+h)-f(x-h)}{2h}=\underset{h\to 0}{\mathop{\frac{1}{2}\lim }}\,\left( \frac{f(x+h)-f(x)}{h}+\frac{f(x-h)-f(x)}{-h} \right)=\frac{1}{2}\left[ {f}'(x)+{f}'(x) \right]={f}'(x)](/forum/ext/geomar/texintegr/latexrender/pictures/2c5288bdaec319c0a59ad68f55eab950.png)
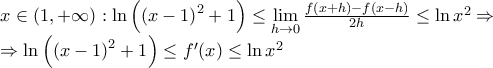
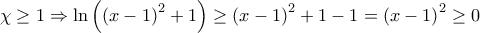
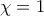 έπεται ότι
έπεται ότι  στο
στο 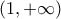
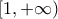
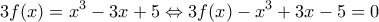 . Προφανής λύση η
. Προφανής λύση η 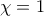
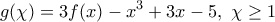 . Τότε
. Τότε 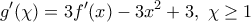
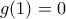 . Έστω ότι υπάρχει
. Έστω ότι υπάρχει 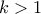 με
με 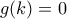
![\displaystyle [1,k] \displaystyle [1,k]](/forum/ext/geomar/texintegr/latexrender/pictures/3a54fcc136ac78b6a6e4e859d5fe90b2.png) υπάρχει ένα
υπάρχει ένα 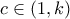 με
με 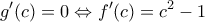
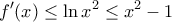 και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για 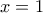 .Άρα δεν υπάρχει
.Άρα δεν υπάρχει 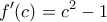 ,
, 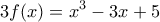 είναι η
είναι η  ορίζεται στο
ορίζεται στο ![\displaystyle [1,x] \displaystyle [1,x]](/forum/ext/geomar/texintegr/latexrender/pictures/1e0642e4779bd410bda492de784d3164.png) ,υπάρχει ένα
,υπάρχει ένα 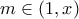 , ώστε
, ώστε 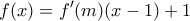
 :
: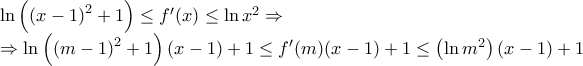
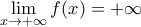 ,
, 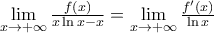
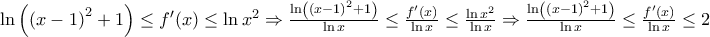
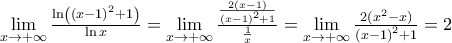 ,οπότε
,οπότε 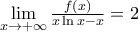
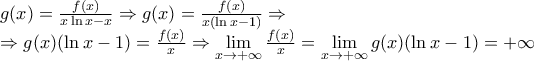
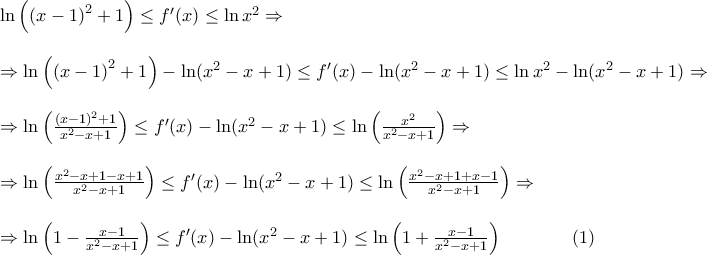
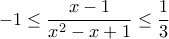
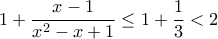 και
και 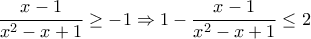 (2)
(2)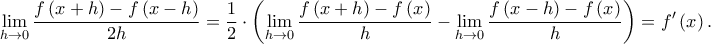
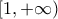 και παραγωγίσιμη στο
και παραγωγίσιμη στο 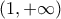 με
με 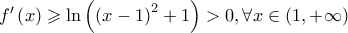 , άρα η
, άρα η 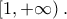 Η
Η 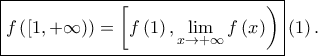 Για κάθε
Για κάθε  η
η ![\left [ 1,x \right ] \left [ 1,x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/560dcdf3db182a4e796d9c084358929c.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 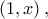 άρα από ΘΜΤ υπάρχει
άρα από ΘΜΤ υπάρχει 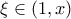 με
με 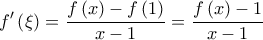 και αφού
και αφού 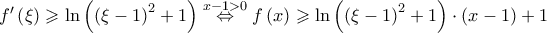 και επειδή
και επειδή ![\displaystyle \lim_{x\rightarrow +\infty}\left [ \ln\left ( \left ( \xi -1 \right )^{2}+1 \right )\cdot \left ( x-1 \right )+1 \right ]=+\infty, \displaystyle \lim_{x\rightarrow +\infty}\left [ \ln\left ( \left ( \xi -1 \right )^{2}+1 \right )\cdot \left ( x-1 \right )+1 \right ]=+\infty,](/forum/ext/geomar/texintegr/latexrender/pictures/fa1f593cc4590045930ad251837ebdde.png) άρα
άρα 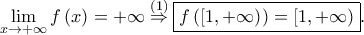
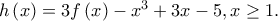 Είναι
Είναι 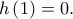 Έστω ότι η
Έστω ότι η  έχει κάποια ρίζα
έχει κάποια ρίζα  Η
Η ![\left [ 1,\rho \right ] \left [ 1,\rho \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/fc66e7bdf92aade6de829530c1a5cc55.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 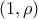 με
με 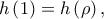 άρα από Θ. Rolle υπάρχει
άρα από Θ. Rolle υπάρχει 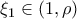 με
με 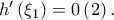 Η
Η 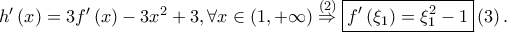 Συνεπώς
Συνεπώς 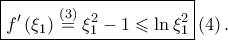 Θεωρούμε την συνάρτηση
Θεωρούμε την συνάρτηση 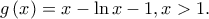 Η
Η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με 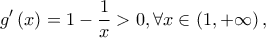 άρα η
άρα η 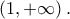 Η
Η 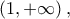 άρα
άρα 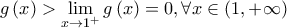 και από την σχέση
και από την σχέση 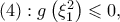 άτοπο. Άρα, η εξίσωση έχει μοναδική λύση στο
άτοπο. Άρα, η εξίσωση έχει μοναδική λύση στο 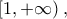 την
την 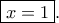
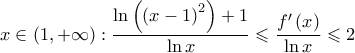 και αφού
και αφού 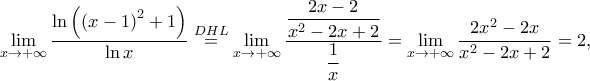 άρα από το Κριτήριο Παρεμβολής
άρα από το Κριτήριο Παρεμβολής 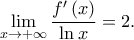 Είναι
Είναι 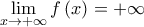 και
και 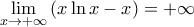 και αφού το όριο
και αφού το όριο 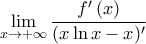 υπάρχει και ισούται με
υπάρχει και ισούται με 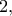 από τον κανόνα De L' Hospital και το όριο
από τον κανόνα De L' Hospital και το όριο 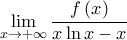 υπάρχει και είναι
υπάρχει και είναι 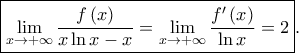
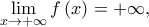 η
η  δεν έχει οριζόντια ασύμπτωτη στο
δεν έχει οριζόντια ασύμπτωτη στο 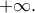 Για κάθε
Για κάθε 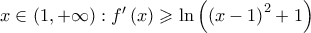 και αφού
και αφού 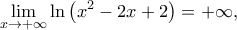 άρα
άρα 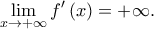 Αφού
Αφού  υπάρχει και ισούται με
υπάρχει και ισούται με 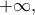 από τον Κανόνα De L' Hospital (το όριο
από τον Κανόνα De L' Hospital (το όριο 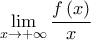 είναι απροσδιόριστη μορφή
είναι απροσδιόριστη μορφή 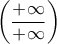 ) και το όριο
) και το όριο 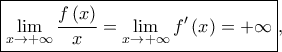 άρα η
άρα η 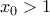 με
με 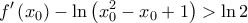 . Αφού
. Αφού 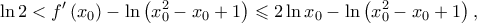 άρα
άρα 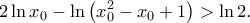 Θεωρούμε την συνάρτηση
Θεωρούμε την συνάρτηση  Η
Η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με 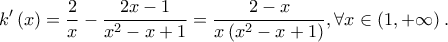 Είναι:
Είναι: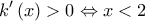
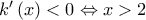
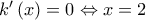
![\left ( 1,2 \right ] \left ( 1,2 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e600b6010271879fe15c690839d810fd.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο 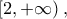 άρα
άρα 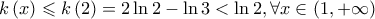 και
και 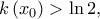 άτοπο.
άτοπο.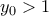 με
με 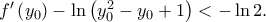 Αφού
Αφού 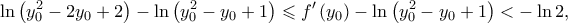 άρα
άρα  Θεωρούμε την συνάρτηση
Θεωρούμε την συνάρτηση 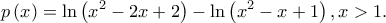 Η
Η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με 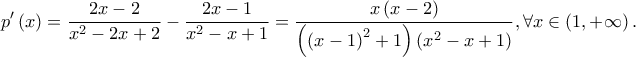 Είναι:
Είναι: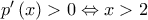
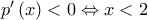
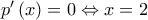
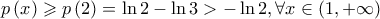 και
και 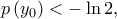 άτοπο.
άτοπο.