 Δίνεται η συνάρτηση :
Δίνεται η συνάρτηση :  .
. Για τις διάφορες τιμές του
 , λύστε την εξίσωση :
, λύστε την εξίσωση :  .
.Συντονιστής: KAKABASBASILEIOS
 Δίνεται η συνάρτηση :
Δίνεται η συνάρτηση :  .
.  , λύστε την εξίσωση :
, λύστε την εξίσωση :  .
. και έχουμε
και έχουμε  όπου
όπου
 σαν τριώνυμο του
σαν τριώνυμο του  με αρνητική διακρίνουσα έχει ελάχιστη τιμή στο
με αρνητική διακρίνουσα έχει ελάχιστη τιμή στο  το
το 
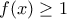 για κάθε
για κάθε  με την ισότητα μόνο για
με την ισότητα μόνο για 
 στο
στο  για
για  Πρέπει να εξετάσουμε για πόσα
Πρέπει να εξετάσουμε για πόσα  το
το  είναι τιμή της
είναι τιμή της 
 και περνάμε στη δεύτερη παράγωγο
και περνάμε στη δεύτερη παράγωγο με αρνητική διακρίνουσα και θετικό συντελεστή στο
με αρνητική διακρίνουσα και θετικό συντελεστή στο 
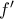 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και άρα έχει το πολύ μια ρίζα. Έύκολά, το
και άρα έχει το πολύ μια ρίζα. Έύκολά, το  είναι ρίζα της
είναι ρίζα της 
 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![\left(-\infty,\frac{1}{2}\right] \left(-\infty,\frac{1}{2}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/14eac180d1c6f929d538f51e76e9d28d.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  όπου το σύνολο τιμών κάθε
όπου το σύνολο τιμών κάθε όπου το
όπου το  ανήκει.
ανήκει. 


 , με την ισότητα για :
, με την ισότητα για :  .
. , η εξίσωση είναι αδύνατη .
, η εξίσωση είναι αδύνατη . , η εξίσωση έχει μία λύση ( την
, η εξίσωση έχει μία λύση ( την  ) .
) . , η εξίσωση έχει δύο λύσεις .
, η εξίσωση έχει δύο λύσεις . ;
;Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες