 ,
,θα προκύψει ακέραιος που να είναι τέλειο τετράγωνο με βάση θετικό ακέραιο.
Συντονιστής: ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
 ,
, έχουμε το εξής:
έχουμε το εξής:
 είναι
είναι 
 . Άρα δεν μας κάνει, γιατί το εν λόγω (αυτό που δίνεται στην εκφώνηση) κλάσμα πρέπει να είναι θετικός ακέραιος!
. Άρα δεν μας κάνει, γιατί το εν λόγω (αυτό που δίνεται στην εκφώνηση) κλάσμα πρέπει να είναι θετικός ακέραιος! και άρα
και άρα 
 . Επομένως έχουμε:
. Επομένως έχουμε:
 για την οποία ισχύει ότι το κλάσμα ισούται με
για την οποία ισχύει ότι το κλάσμα ισούται με  και άρα είναι τέλειο τετράγωνο θετικού ακεραίου
και άρα είναι τέλειο τετράγωνο θετικού ακεραίου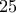
 ο ζητούμενος ακέραιος. Θέλουμε
ο ζητούμενος ακέραιος. Θέλουμε  , όπου
, όπου  θετικός ακέραιος.
θετικός ακέραιος. , δηλαδή
, δηλαδή  και άρα
και άρα  . (1)
. (1) , βλέπουμε ότι η εξίσωση (1) είναι αδύνατη. Με
, βλέπουμε ότι η εξίσωση (1) είναι αδύνατη. Με  , η (1) γράφεται:
, η (1) γράφεται:

 ακέραιος, πρέπει ο αριθμός
ακέραιος, πρέπει ο αριθμός  να είναι διαιρέτης του
να είναι διαιρέτης του 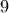
 , ή
, ή  , , ή
, , ή  , ή
, ή  , ή
, ή  , ή
, ή 
 είναι θετικός ακέραιος), από τις πιο πάνω εξισώσεις, δεκτή είναι μόνο η
είναι θετικός ακέραιος), από τις πιο πάνω εξισώσεις, δεκτή είναι μόνο η  , από την οποία προκύπτει
, από την οποία προκύπτει και από την (1) έχουμε
και από την (1) έχουμε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης