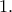 Να βρείτε όλους τους θετικούς ακεραίους
Να βρείτε όλους τους θετικούς ακεραίους  για τους οποίους
για τους οποίους 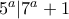
 Να βρείτε όλoυς τoυς πρώτους
Να βρείτε όλoυς τoυς πρώτους  που ικανοποιούν την
που ικανοποιούν την 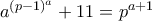 , όπου
, όπου  o προαναφερθείς θετικός ακέραιος. Για μαθητές
o προαναφερθείς θετικός ακέραιος. Για μαθητέςΣυντονιστές: cretanman, silouan, rek2
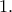 Να βρείτε όλους τους θετικούς ακεραίους
Να βρείτε όλους τους θετικούς ακεραίους  για τους οποίους
για τους οποίους 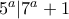
 Να βρείτε όλoυς τoυς πρώτους
Να βρείτε όλoυς τoυς πρώτους  που ικανοποιούν την
που ικανοποιούν την 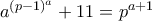 , όπου
, όπου  o προαναφερθείς θετικός ακέραιος. Για μαθητές
o προαναφερθείς θετικός ακέραιος. Για μαθητές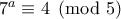
 με το
με το  είναι τα (
είναι τα ( ) τα οποία επαναλαμβάνονται. Άρα για να ισχύει ότι
) τα οποία επαναλαμβάνονται. Άρα για να ισχύει ότι 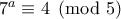 , πρέπει
, πρέπει 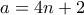 , δηλαδή
, δηλαδή  άρτιος, έστω
άρτιος, έστω 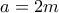 , με
, με 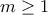 .
.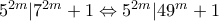 . Έστω
. Έστω 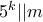 . Επειδή
. Επειδή 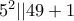 , από το θεώρημα
, από το θεώρημα  παίρνουμε ότι:
παίρνουμε ότι: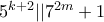 . Πρέπει να ισχύει ότι
. Πρέπει να ισχύει ότι 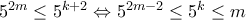 , άρα αναγκαστικά
, άρα αναγκαστικά  , δηλαδή
, δηλαδή 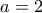 , όπου εγκρίνεται.
, όπου εγκρίνεται.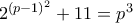
 δεν έχουμε λύσεις.
δεν έχουμε λύσεις. περιττός, δηλαδή
περιττός, δηλαδή 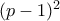 άρτιος.
άρτιος.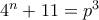
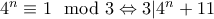 , άρα
, άρα 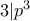 , που σημαίνει ότι
, που σημαίνει ότι  , που εγκρίνεται.
, που εγκρίνεται.Εννοώ ότι δεν είναι πάρα πολύ απλή για Juniors...JimNt. έγραψε:Σε ποιο σημείο αναφέρεσαι;
ΒασικάΔιονύσιος Αδαμόπουλος έγραψε:Δεν την λες και πολύ απλή...
1. Πρέπει να ισχύει ότι
Παρατηρούμε πως τα υπόλοιπα που αφήνει μια δύναμη τουμε το
είναι τα (
) τα οποία επαναλαμβάνονται. Άρα για να ισχύει ότι
, πρέπει
, δηλαδή
άρτιος, έστω
, με
.
Άρα η εξίσωση γίνεται:
. Έστω
. Επειδή
, από το θεώρημα
παίρνουμε ότι:
. Πρέπει να ισχύει ότι
, άρα αναγκαστικά
, δηλαδή
, όπου εγκρίνεται.
2. Η εξίσωση γίνεται:
Γιαδεν έχουμε λύσεις.
Άραπεριττός, δηλαδή
άρτιος.
Επομένως η εξίσωση γίνεται:
Όμως, άρα
, που σημαίνει ότι
, που εγκρίνεται.
Edit: Προστέθηκε και το 2 ερώτημα.
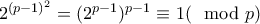

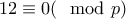 .....
.....Συνεπώς αν δεν κανω κάποιο λαθος εκ παραδρομής ισχύει για καθεJimNt. έγραψε:ΒασικάΔιονύσιος Αδαμόπουλος έγραψε:Δεν την λες και πολύ απλή...
1. Πρέπει να ισχύει ότι
Παρατηρούμε πως τα υπόλοιπα που αφήνει μια δύναμη τουμε το
είναι τα (
) τα οποία επαναλαμβάνονται. Άρα για να ισχύει ότι
, πρέπει
, δηλαδή
άρτιος, έστω
, με
.
Άρα η εξίσωση γίνεται:
. Έστω
. Επειδή
, από το θεώρημα
παίρνουμε ότι:
. Πρέπει να ισχύει ότι
, άρα αναγκαστικά
, δηλαδή
, όπου εγκρίνεται.
2. Η εξίσωση γίνεται:
Γιαδεν έχουμε λύσεις.
Άραπεριττός, δηλαδή
άρτιος.
Επομένως η εξίσωση γίνεται:
Όμως, άρα
, που σημαίνει ότι
, που εγκρίνεται.
Edit: Προστέθηκε και το 2 ερώτημα.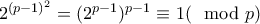

.....

Σωστά.ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Συνεπώς αν δεν κανω κάποιο λαθος εκ παραδρομής ισχύει για καθεJimNt. έγραψε:ΒασικάΔιονύσιος Αδαμόπουλος έγραψε:Δεν την λες και πολύ απλή...
1. Πρέπει να ισχύει ότι
Παρατηρούμε πως τα υπόλοιπα που αφήνει μια δύναμη τουμε το
είναι τα (
) τα οποία επαναλαμβάνονται. Άρα για να ισχύει ότι
, πρέπει
, δηλαδή
άρτιος, έστω
, με
.
Άρα η εξίσωση γίνεται:
. Έστω
. Επειδή
, από το θεώρημα
παίρνουμε ότι:
. Πρέπει να ισχύει ότι
, άρα αναγκαστικά
, δηλαδή
, όπου εγκρίνεται.
2. Η εξίσωση γίνεται:
Γιαδεν έχουμε λύσεις.
Άραπεριττός, δηλαδή
άρτιος.
Επομένως η εξίσωση γίνεται:
Όμως, άρα
, που σημαίνει ότι
, που εγκρίνεται.
Edit: Προστέθηκε και το 2 ερώτημα.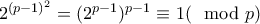

.....

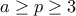 τότε:
τότε: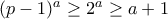 ,
,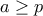
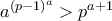 δηλαδή
δηλαδή 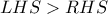
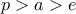 και
και  έχω:
έχω: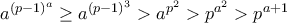 δηλαδή
δηλαδή 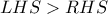
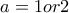 και
και 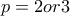 που δεν είναι δύσκολες
που δεν είναι δύσκολες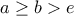 με
με  πραγματικούς τότε :
πραγματικούς τότε :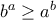
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες