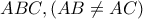 και έστω
και έστω  το ορθόκεντρο και
το ορθόκεντρο και  το μέσο του μεγάλου τόξου
το μέσο του μεγάλου τόξου 
του περίκυκλού του. Επί των πλευρών
 θεωρούμε τα σημεία
θεωρούμε τα σημεία 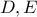 αντίστοιχα, ώστε η
αντίστοιχα, ώστε η  να διέρχεται
να διέρχεται από το
 και να είναι
και να είναι  . Να δείξετε ότι η
. Να δείξετε ότι η 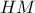 διέρχεται από το περίκεντρο
διέρχεται από το περίκεντρο  του τριγώνου
του τριγώνου 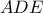 .
.Συντονιστές: vittasko, silouan, Doloros
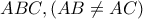 και έστω
και έστω  το ορθόκεντρο και
το ορθόκεντρο και  το μέσο του μεγάλου τόξου
το μέσο του μεγάλου τόξου 
 θεωρούμε τα σημεία
θεωρούμε τα σημεία 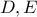 αντίστοιχα, ώστε η
αντίστοιχα, ώστε η  να διέρχεται
να διέρχεται  και να είναι
και να είναι  . Να δείξετε ότι η
. Να δείξετε ότι η 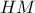 διέρχεται από το περίκεντρο
διέρχεται από το περίκεντρο  του τριγώνου
του τριγώνου 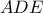 .
. το μέσο του
το μέσο του  και
και  το διαμετρικό του
το διαμετρικό του  . Επίσης έστω
. Επίσης έστω  . Αφού τα
. Αφού τα 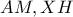 είναι παράλληλα και αντίρροπα, το
είναι παράλληλα και αντίρροπα, το  είναι εσωτερικό του
είναι εσωτερικό του  .
.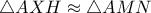 οπότε
οπότε 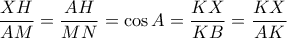 .
.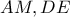 ισχύει
ισχύει 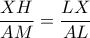 . Άρα
. Άρα 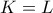 αφού τα
αφού τα  είναι εσωτερικά του
είναι εσωτερικά του  .
.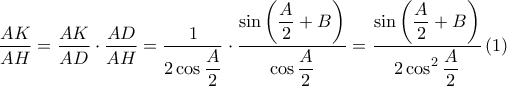
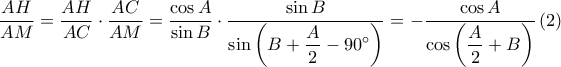
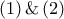 έπεται ότι
έπεται ότι 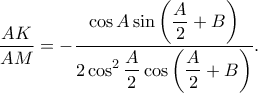
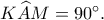 Συνεπώς, είναι
Συνεπώς, είναι 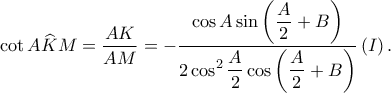
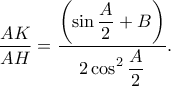
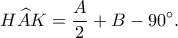 Επομένως έχουμε
Επομένως έχουμε 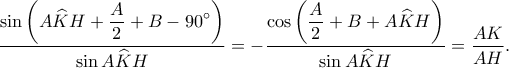
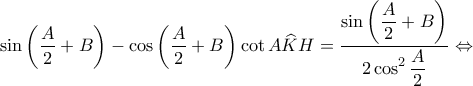
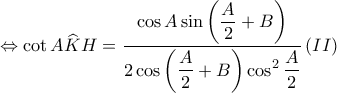
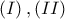 είναι
είναι 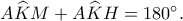
 σκαληνό τρίγωνο και
σκαληνό τρίγωνο και  μια ευθεία που διέρχεται από το ορθόκεντρο
μια ευθεία που διέρχεται από το ορθόκεντρο  . Έστω ότι η
. Έστω ότι η  τέμνει την
τέμνει την  στο
στο  και την
και την  στο
στο  . Αν
. Αν  είναι το περίκεντρο του περιγεγραμμένου κύκλου του τριγώνου
είναι το περίκεντρο του περιγεγραμμένου κύκλου του τριγώνου  και
και  τέμνει τον περίγεγραμμένο κύκλο του
τέμνει τον περίγεγραμμένο κύκλο του  στο
στο  , να αποδειχθεί ότι δια του
, να αποδειχθεί ότι δια του  κάθετη στην BC και η
κάθετη στην BC και η  τέμνονται στον περιγεγραμμένο κύκλο του
τέμνονται στον περιγεγραμμένο κύκλο του  .
.Καλησπέρα! Ωραίο και δύσκολο. Δίνω τη λύση μου. Έστω R η δεύτερη τομή της εκ του F κάθετης στην ΒC με τον κύκλο (ABC).Κω.Κωνσταντινίδης έγραψε: ↑Τετ Ιουν 14, 2023 6:25 pmΙσχύει και η παρακάτω γενίκευση:
Έστωσκαληνό τρίγωνο και
μια ευθεία που διέρχεται από το ορθόκεντρο
. Έστω ότι η
τέμνει την
στο
και την
στο
. Αν
είναι το περίκεντρο του περιγεγραμμένου κύκλου του τριγώνου
και
τέμνει τον περίγεγραμμένο κύκλο του
στο
, να αποδειχθεί ότι δια του
κάθετη στην BC και η
τέμνονται στον περιγεγραμμένο κύκλο του
.
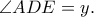 Είναι από νόμους ημιτόνων κλπ
Είναι από νόμους ημιτόνων κλπ 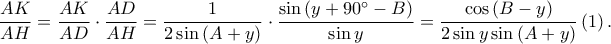
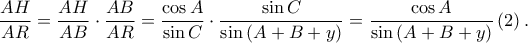
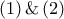 προκύπτει πως
προκύπτει πως 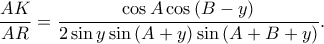
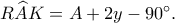 Συνεπώς, έχουμε
Συνεπώς, έχουμε 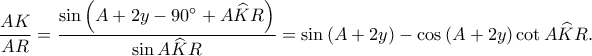
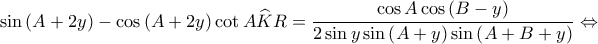
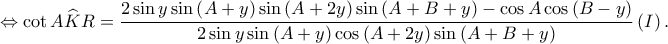
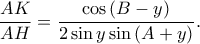
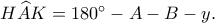 Συνεπώς, είναι
Συνεπώς, είναι 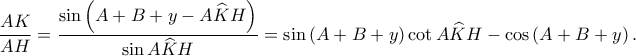
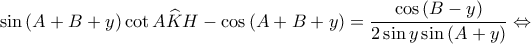
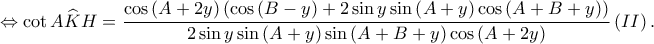
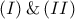 συμπεραίνουμε ότι
συμπεραίνουμε ότι 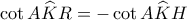 οπότε
οπότε 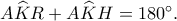
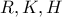 είναι συνευθειακά που ολοκληρώνει την απόδειξη.
είναι συνευθειακά που ολοκληρώνει την απόδειξη.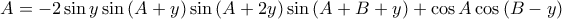
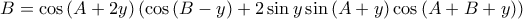
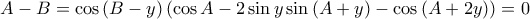
 ,
, 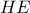 είναι διχοτόμοι των κατακορυφήν γωνιών
είναι διχοτόμοι των κατακορυφήν γωνιών 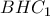 ,
, 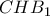 αντίστοιχα.
αντίστοιχα. 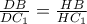 και
και 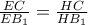 .
.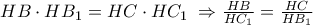 . Ως εκ τούτου,
. Ως εκ τούτου, 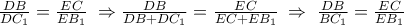 .
.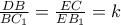 . Τότε
. Τότε 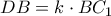 και
και 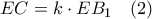 .
. και
και  κινούνται με σταθερές ταχύτητες (όχι αναγκαία ίσες) σε δύο σταθερές ευθείες που τέμνονται
κινούνται με σταθερές ταχύτητες (όχι αναγκαία ίσες) σε δύο σταθερές ευθείες που τέμνονται  . Να αποδείξετε ότι ο περιγεγραμμένος κύκλος του τριγώνου
. Να αποδείξετε ότι ο περιγεγραμμένος κύκλος του τριγώνου 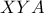 , διέρχεται από δύο σταθερά σημεία
, διέρχεται από δύο σταθερά σημεία  και
και  , όπου το
, όπου το  είναι το κέντρο της σπειροειδούς ομοιότητας που μετασχηματίζει τα σημεία
είναι το κέντρο της σπειροειδούς ομοιότητας που μετασχηματίζει τα σημεία  στα σημεία
στα σημεία  .
. ,
,  βρίσκονται στις θέσεις των κορυφών
βρίσκονται στις θέσεις των κορυφών  ,
,  αντίστοιχα. Μετά παρέλευση χρόνου
αντίστοιχα. Μετά παρέλευση χρόνου 
 ,
,  , οπότε σύμφωνα με τις σχέσεις
, οπότε σύμφωνα με τις σχέσεις  , μετά παρέλευση χρόνου
, μετά παρέλευση χρόνου 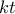 τα
τα  ,
,  θα βρίσκονται στις θέσεις
θα βρίσκονται στις θέσεις  ,
,  αντίστοιχα. Ως εκ τούτου, οι κύκλοι
αντίστοιχα. Ως εκ τούτου, οι κύκλοι 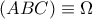 ,
, 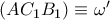 και
και 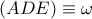 θα διέρχονται από τα σημεία
θα διέρχονται από τα σημεία  ,
,  .
. ,
,  ,
,  τα κέντρα των κύκλων
τα κέντρα των κύκλων  ,
,  ,
, 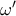 αντίστοιχα. Τότε
αντίστοιχα. Τότε 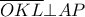 (η διάκεντρος είναι κάθετος στην κοινή χορδή των κύκλων).
(η διάκεντρος είναι κάθετος στην κοινή χορδή των κύκλων).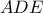 το περίκεντρο
το περίκεντρο  αυτού του τριγώνου ανήκει στη διχοτόμο της γωνίας
αυτού του τριγώνου ανήκει στη διχοτόμο της γωνίας  , η οποία
, η οποία  του
του  στο αντιδιαμετρικό σημείο
στο αντιδιαμετρικό σημείο  του
του  .
. είναι διάμετρος του κύκλου
είναι διάμετρος του κύκλου 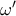 (
(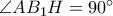 ), τότε
), τότε 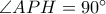 . Επομένως, το σημείο τομής
. Επομένως, το σημείο τομής  της ευθείας
της ευθείας 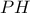
 θα είναι το αντιδιαμετρικό της κορυφής
θα είναι το αντιδιαμετρικό της κορυφής  σε αυτόν τον κύκλο.
σε αυτόν τον κύκλο. του τριγώνου
του τριγώνου  ως προς το μέσο
ως προς το μέσο 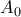 της πλευράς
της πλευράς  είναι
είναι  . Ως εκ τούτου, τα σημεία
. Ως εκ τούτου, τα σημεία  ,
,  ,
, 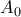 ,
,  ανήκουν στην ίδια ευθεία.
ανήκουν στην ίδια ευθεία.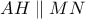 . Εφόσον
. Εφόσον 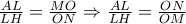 , οπότε σύμφωνα με το αντίστροφο του θεωρήματος της δέσμης ευθειών,
, οπότε σύμφωνα με το αντίστροφο του θεωρήματος της δέσμης ευθειών,  ,
,  ,
, 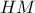 αποτελούν δέσμη, και εφόσον
αποτελούν δέσμη, και εφόσον 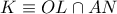 , τότε και η
, τότε και η 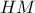 διέρχεται από το
διέρχεται από το  .
.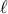 μια ευθεία που διέρχεται από το ορθόκεντρο H.
μια ευθεία που διέρχεται από το ορθόκεντρο H. 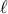 τέμνει την AB στο E και την AC στο F. Αν K είναι το περίκεντρο
τέμνει την AB στο E και την AC στο F. Αν K είναι το περίκεντρο  τέμνει το τόξο
τέμνει το τόξο  του κύκλου
του κύκλου 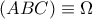 σε σημείο
σε σημείο  , έτσι ώστε
, έτσι ώστε 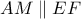 .
. που άγεται από το σημείο
που άγεται από το σημείο  τέμνει το τόξο
τέμνει το τόξο  του κύκλου
του κύκλου 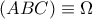
 , έτσι ώστε
, έτσι ώστε 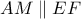 .
Απόδειξη: Η
.
Απόδειξη: Η  τέμνει τον κύκλο
τέμνει τον κύκλο 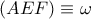 στο σημείο
στο σημείο  . Τότε,
. Τότε,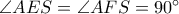 (
( διάμετρος του
διάμετρος του  ).
).  ,
,  οι προβολές του
οι προβολές του  στις
στις  ,
,  αντίστοιχα. Τότε, η ευθεία
αντίστοιχα. Τότε, η ευθεία  είναι η ευθεία Simson
είναι η ευθεία Simson  στον κύκλο
στον κύκλο  , Αν
, Αν 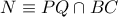 , τότε
, τότε 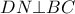 . και έστω
. και έστω  το σημείο τομής της ευθεία
το σημείο τομής της ευθεία 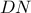
 του κύκλου
του κύκλου  .
.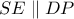 και
και 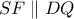 είναι:
είναι: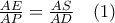 και
και 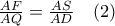
 ,
,  προκύπτει ότι
προκύπτει ότι 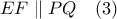 .
.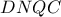 είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε 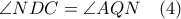 . Αλλά
. Αλλά 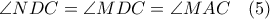 .
. ,
, 
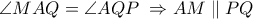 , και λόγω της
, και λόγω της 
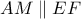 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης