viewtopic.php?f=184&t=74621
Εστω
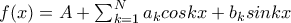
όπου
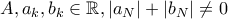
Αν ισχύει
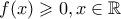
τότε ισχύει
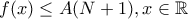
Η τελευταία ανισότητα είναι η καλύτερη δυνατή.
Συντονιστές: achilleas, emouroukos, silouan
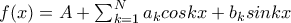
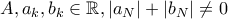
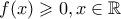
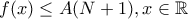
Θα βγω εκτός φακέλου.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Οκτ 15, 2023 12:50 pmΜε αφορμή το
viewtopic.php?f=184&t=74621
Εστω
όπου
Αν ισχύει
τότε ισχύει
Η τελευταία ανισότητα είναι η καλύτερη δυνατή.
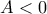 γιατί τότε, ολοκληρώνοντας στο
γιατί τότε, ολοκληρώνοντας στο ![[0,2\pi] [0,2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) θα παίρναμε ότι η
θα παίρναμε ότι η  έχει αρνητική μέση τιμή και επομένως παίρνει και αρνητικές τιμές, πράγμα άτοπο.
έχει αρνητική μέση τιμή και επομένως παίρνει και αρνητικές τιμές, πράγμα άτοπο.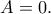 Τότε θα είχαμε ότι η μέση τιμή είναι
Τότε θα είχαμε ότι η μέση τιμή είναι  οπότε θα ήταν σταθερή
οπότε θα ήταν σταθερή 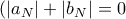 άτοπο) ή, αν δεν ήταν σταθερή θα έπαιρνε και αρνητικές τιμές (άτοπο).
άτοπο) ή, αν δεν ήταν σταθερή θα έπαιρνε και αρνητικές τιμές (άτοπο).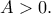 Από εκεί και πέρα η απόδειξη που έκανα στο σύνδεσμο γενικεύεται.
Από εκεί και πέρα η απόδειξη που έκανα στο σύνδεσμο γενικεύεται. 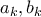 να υποθέσουμε
να υποθέσουμε 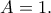
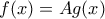 με
με 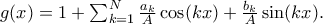
 και
και 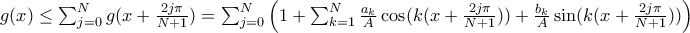
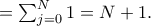
 παίρνουμε τη ζητούμενη ανισότητα για την
παίρνουμε τη ζητούμενη ανισότητα για την 
 . Μπορούμε κατευθείαν να πάρουμε στα δεξιά άθροισμα στην
. Μπορούμε κατευθείαν να πάρουμε στα δεξιά άθροισμα στην  και να μην θεωρήσουμε την
και να μην θεωρήσουμε την  . Ο μόνος λόγος είναι για να συμβαδίζει η εδώ απόδειξη με την απόδειξη της παραπομπής
. Ο μόνος λόγος είναι για να συμβαδίζει η εδώ απόδειξη με την απόδειξη της παραπομπής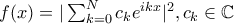
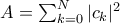
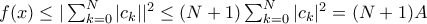

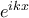 αρκεί να το αντικαταστήσει με
αρκεί να το αντικαταστήσει με 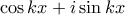
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες