Στον διαγωνισμό
Romanian District Mathematical Olympiad προτάθηκε το 2022
το εξής πρόβλημα:
Romanian District Mathematical Olympiad 2022 έγραψε: Να προσδιορίσετε όλες τις συναρτήσεις

που ικανοποιούν την ισότητα

,
για κάθε

.
Στο
τεύχος 127 του Ευκλείδη Β', προτάθηκε η ίδια άσκηση στις Ασκήσεις για λύση (σελ. 14), αλλά ξέφυγε μια
αθώα παρένθεση και τοποθετήθηκε αλλού, ίσως εκ παραδρομής:
Ευκλείδης Β', Τεύχος 127 έγραψε: Να προσδιορίσετε όλες τις συναρτήσεις

που ικανοποιούν την ισότητα

,
για κάθε

.
Πιστεύω ότι το δεύτερο πρόβλημα είναι αρκετά δυσκολότερο από το πρώτο. Ας λύσουμε και τα δύο

που ικανοποιούν την ισότητα
,
.
που ικανοποιούν την ισότητα
,
.

 η δοσμένη σχέση,
η δοσμένη σχέση, .
.

 .
. τότε η παραπάνω δίνει άμεσα ότι
τότε η παραπάνω δίνει άμεσα ότι  είναι
είναι  και επί στο
και επί στο  .
. δίνει
δίνει  , θέτω
, θέτω  και παίρνω
και παίρνω  και με αφαίρεση από την προηγούμενη έχω τελικά
και με αφαίρεση από την προηγούμενη έχω τελικά  .
. γίνεται
γίνεται 
 σε αυτή παίρνω
σε αυτή παίρνω 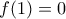 .
. και έτσι
και έτσι  δηλαδή
δηλαδή  αλλά
αλλά  άτοπο.
άτοπο. άρα
άρα  άρα
άρα 

 είναι
είναι  .
. είναι
είναι  που με
που με  δίνει ότι
δίνει ότι  και αφού
και αφού  , με
, με  παίρνουμε
παίρνουμε  όπως θέλαμε.
όπως θέλαμε. .
. άρα
άρα  για
για  και αφού η
και αφού η 
 .
. δουλεύει και επομένως
δουλεύει και επομένως  για κάθε
για κάθε  .
.