ΓΡΗΓΟΡΗ ΑΠΑΝΤΗΣΗ
Από τα σημεία
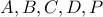
διέρχεται μοναδική κωνική τομή που υπό τα δεδομένα του προβλήματος είναι μια υπερβολή. Οι υποθέσεις του προβλήματος καθιστούν το

επίσης σημείο αυτής της υπερβολής. Λόγω του
hexagrammum mysticum theorem του Pascal (
https://en.wikipedia.org/wiki/Pascal's_theorem) τα
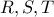
θα πρέπει να είναι συνευθειακά.
ΑΝΑΛΥΤΙΚΗ ΑΠΑΝΤΗΣΗ
Κατ' αρχάς αξίζει να σημειώσουμε ότι για την ισχύ του ζητουμένου δεν είναι αναγκαίο τα σημεία

να βρίσκονται στο εσωτερικό του τραπεζίου

. Ειδικότερα δεν είναι αναγκαίο να ορίζονται οι ευθείες
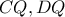
. Επίσης η κλειστή τεθλασμένη
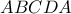
δεν είναι απαραίτητο να είναι απλή. Θα επαναδιατυπώσουμε το πρόβλημα ζητώντας:
i) τα

να είναι διαφορετικά ανά δυο,

και οι ευθείες
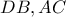
να τέμνονται στο

.
ii) το

να είναι οποιοδήποτε σημείο του επιπέδου με την εξαίρεση των σημείων:
1) της ευθείας

. Αν
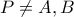
τότε ορίζονται οι ευθείες
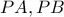
. Αν το

δεν είναι σημείο της

τότε οι ευθείες αυτές δεν είναι παράλληλες και οι (μοναδικές) παράλληλες από το

στην

και από το

στην
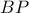
τέμνονται σε μοναδικό σημείο, το

. Έτσι λοιπόν το

καθορίζει το

με μοναδικό τρόπο αποτελώντας τη μοναδική ελεύθερη παράμετρο του προβλήματος.
2) 
προκειμένου αφ' ενός να ορίζονται αντίστοιχα οι ευθείες
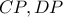
, αφ' ετέρου να ορίζονται αντίστοιχα οι ευθείες
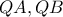
.
3) του γεωμετρικού τόπου των

για τα οποία
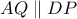
(για να ορίζεται το

)
4) του γεωμετρικού τόπου των

για τα οποία
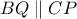
(για να ορίζεται το

)
Υπό τις παραπάνω συνθήκες θα αποδείξουμε ότι τα
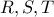
είναι συνευθειακά (δεν αναφερόμαστε σε ευθεία
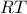
γιατί αυτή δεν ορίζεται για κάθε

π.χ. αν
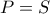
τότε
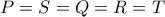
).
Στην παρούσα λύση δε θα μελετήσουμε τις ιδιότητες των τόπων που αναφέρονται στα 3),4). Θα αρκεστούμε να αναφέρουμε πως αν συμπεριλάβουμε σε αυτούς τα εξαιρεμένα σημεία

, καθένας από αυτούς καθίσταται μια κωνική τομή. Συγκεκριμένα ο Γ.Τ. στο 3) δίνει την κωνική τομή που διέρχεται από τα

και της οποίας η εφαπτομένη στο

είναι παράλληλη στην ευθεία

, ενώ ο Γ.Τ. στο 4) δίνει την κωνική τομή που διέρχεται από τα

και της οποίας η εφαπτομένη στο

είναι παράλληλη στην ευθεία

.
Θα προχωρήσουμε τώρα στην απάντηση του προβλήματος.
Με εφαρμογή ενός κατάλληλου αφφινικού μετασχηματισμού αρκεί να θεωρήσουμε ότι
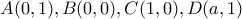
με
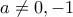
. Έστω επίσης σημείο
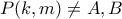
.
Θεωρούμε τις ευθείες
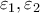
, τις μοναδικές παράλληλες αντίστοιχα από το

στην

και από το

στην
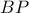
.
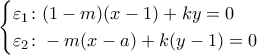
Αν το

βρίσκεται εκτός της ευθείας

(

) οι
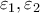
θα τέμνονται σε μοναδικό σημείο

με συντεταγμένες
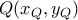
με
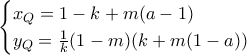
Στο σημείο που βρισκόμαστε κανείς θα μπορούσε να προχωρήσει με αναλυτικό brute force, να υπολογίσει τις συντεταγμένες των
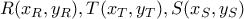
και να δείξει ότι είναι συνευθειακά σημεία επαληθεύοντας την ισχύ της ισότητας
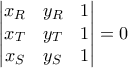
. Μια τέτοια προσέγγιση στην παρούσα ανάρτηση είναι άνευ νοήματος, οπότε θα προχωρήσουμε γεωμετρικότερα κρατώντας τις πράξεις στο ελάχιστο δυνατό.
Έστω επιπλέον ότι
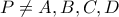
. Θεωρούμε τη (μοναδική μεν, ενδεχομένως εκφυλισμένη δε) κωνική τομή που διέρχεται από τα
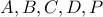
με εξίσωση
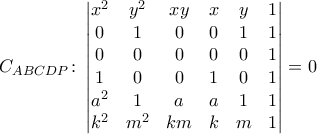
.
Με λίγες πράξεις διαπιστώνει κανείς ότι το

είναι επίσης σημείο της κωνικής τομής
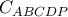
Γνωρίζουμε ότι
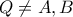
οπότε διακρίνουμε τις εξής περιπτώσεις:
1)
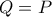
οπότε επειδή
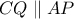
θα πρέπει

συνευθειακά και ομοίως
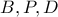
συνευθειακά οπότε
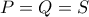
. Βρίσκουμε συνεπώς ότι
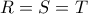
και το ζητούμενο ισχύει τετριμμένα.
2)
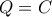
οπότε
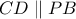
,
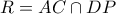
και
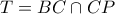
και συνεπώς
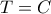
. Παρατηρούμε λοιπόν ότι
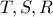
είναι σημεία της ευθείας

οπότε το ζητούμενο ισχύει.
3)
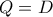
οπότε
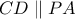
,
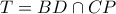
και
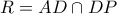
και συνεπώς
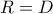
. Παρατηρούμε λοιπόν ότι
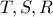
είναι σημεία της ευθείας

οπότε το ζητούμενο ισχύει.
4)
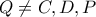
οπότε έχουμε μια εξάδα σημείων που βρίσκονται στην ίδια κωνική τομή. Αν οι ευθείες
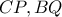
τέμνονται στο

και οι ευθείες
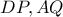
τέμνονται στο

, τότε μπορούμε να επικαλεστούμε το
hexagrammum mysticum theorem του Pascal (
https://en.wikipedia.org/wiki/Pascal's_theorem) από το οποίο πάλι έπεται το ζητούμενο.

 με
με  και έστω
και έστω 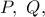 τυχόντα σημεία στο εσωτερικό του ώστε να είναι
τυχόντα σημεία στο εσωτερικό του ώστε να είναι 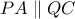 και
και 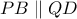 . Απόδείξτε ότι η ευθεία
. Απόδείξτε ότι η ευθεία 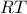 , όπου
, όπου 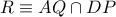 και
και 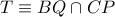 περνάει από το σημείο
περνάει από το σημείο 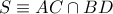 .
Κώστας Βήττας
.
Κώστας Βήττας
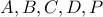 διέρχεται μοναδική κωνική τομή που υπό τα δεδομένα του προβλήματος είναι μια υπερβολή. Οι υποθέσεις του προβλήματος καθιστούν το
διέρχεται μοναδική κωνική τομή που υπό τα δεδομένα του προβλήματος είναι μια υπερβολή. Οι υποθέσεις του προβλήματος καθιστούν το  επίσης σημείο αυτής της υπερβολής. Λόγω του
επίσης σημείο αυτής της υπερβολής. Λόγω του 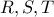 θα πρέπει να είναι συνευθειακά.
θα πρέπει να είναι συνευθειακά. να βρίσκονται στο εσωτερικό του τραπεζίου
να βρίσκονται στο εσωτερικό του τραπεζίου 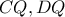 . Επίσης η κλειστή τεθλασμένη
. Επίσης η κλειστή τεθλασμένη 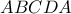 δεν είναι απαραίτητο να είναι απλή. Θα επαναδιατυπώσουμε το πρόβλημα ζητώντας:
δεν είναι απαραίτητο να είναι απλή. Θα επαναδιατυπώσουμε το πρόβλημα ζητώντας: να είναι διαφορετικά ανά δυο,
να είναι διαφορετικά ανά δυο, 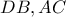 να τέμνονται στο
να τέμνονται στο  .
. να είναι οποιοδήποτε σημείο του επιπέδου με την εξαίρεση των σημείων:
να είναι οποιοδήποτε σημείο του επιπέδου με την εξαίρεση των σημείων:  . Αν
. Αν 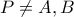 τότε ορίζονται οι ευθείες
τότε ορίζονται οι ευθείες 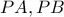 . Αν το
. Αν το  στην
στην  και από το
και από το  στην
στην 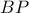 τέμνονται σε μοναδικό σημείο, το
τέμνονται σε μοναδικό σημείο, το  προκειμένου αφ' ενός να ορίζονται αντίστοιχα οι ευθείες
προκειμένου αφ' ενός να ορίζονται αντίστοιχα οι ευθείες 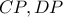 , αφ' ετέρου να ορίζονται αντίστοιχα οι ευθείες
, αφ' ετέρου να ορίζονται αντίστοιχα οι ευθείες 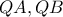 .
.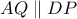 (για να ορίζεται το
(για να ορίζεται το  )
)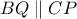 (για να ορίζεται το
(για να ορίζεται το  )
)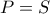 τότε
τότε 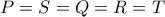 ).
).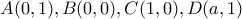 με
με 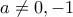 . Έστω επίσης σημείο
. Έστω επίσης σημείο 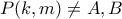 .
.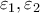 , τις μοναδικές παράλληλες αντίστοιχα από το
, τις μοναδικές παράλληλες αντίστοιχα από το 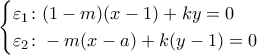
 ) οι
) οι 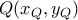 με
με 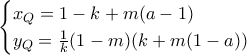
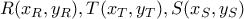 και να δείξει ότι είναι συνευθειακά σημεία επαληθεύοντας την ισχύ της ισότητας
και να δείξει ότι είναι συνευθειακά σημεία επαληθεύοντας την ισχύ της ισότητας 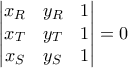 . Μια τέτοια προσέγγιση στην παρούσα ανάρτηση είναι άνευ νοήματος, οπότε θα προχωρήσουμε γεωμετρικότερα κρατώντας τις πράξεις στο ελάχιστο δυνατό.
. Μια τέτοια προσέγγιση στην παρούσα ανάρτηση είναι άνευ νοήματος, οπότε θα προχωρήσουμε γεωμετρικότερα κρατώντας τις πράξεις στο ελάχιστο δυνατό.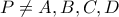 . Θεωρούμε τη (μοναδική μεν, ενδεχομένως εκφυλισμένη δε) κωνική τομή που διέρχεται από τα
. Θεωρούμε τη (μοναδική μεν, ενδεχομένως εκφυλισμένη δε) κωνική τομή που διέρχεται από τα 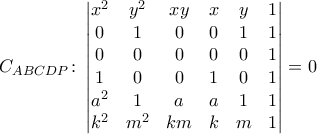 .
.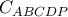
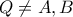 οπότε διακρίνουμε τις εξής περιπτώσεις:
οπότε διακρίνουμε τις εξής περιπτώσεις: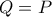 οπότε επειδή
οπότε επειδή 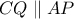 θα πρέπει
θα πρέπει  συνευθειακά και ομοίως
συνευθειακά και ομοίως 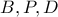 συνευθειακά οπότε
συνευθειακά οπότε 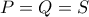 . Βρίσκουμε συνεπώς ότι
. Βρίσκουμε συνεπώς ότι 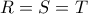 και το ζητούμενο ισχύει τετριμμένα.
και το ζητούμενο ισχύει τετριμμένα.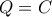 οπότε
οπότε 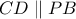 ,
, 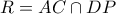 και
και 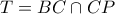 και συνεπώς
και συνεπώς 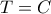 . Παρατηρούμε λοιπόν ότι
. Παρατηρούμε λοιπόν ότι 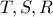 είναι σημεία της ευθείας
είναι σημεία της ευθείας  οπότε το ζητούμενο ισχύει.
οπότε το ζητούμενο ισχύει.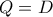 οπότε
οπότε 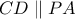 ,
, 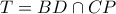 και
και 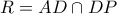 και συνεπώς
και συνεπώς 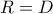 . Παρατηρούμε λοιπόν ότι
. Παρατηρούμε λοιπόν ότι  οπότε το ζητούμενο ισχύει.
οπότε το ζητούμενο ισχύει.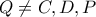 οπότε έχουμε μια εξάδα σημείων που βρίσκονται στην ίδια κωνική τομή. Αν οι ευθείες
οπότε έχουμε μια εξάδα σημείων που βρίσκονται στην ίδια κωνική τομή. Αν οι ευθείες 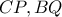 τέμνονται στο
τέμνονται στο 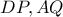 τέμνονται στο
τέμνονται στο 