Henri van Aubel έγραψε: ↑Παρ Ιούλ 14, 2023 5:27 pm
Έστω οξυγώνιο τρίγωνο

με

και περίκεντρο

, ύψος

και

το μέσο της πλευράς

. Οι

και

τέμνονται στο σημείο

και ο περίκυκλος του τριγώνου

επανατέμενει την

στο σημείο

και την ευθεία

στο σημείο

. Να δείξετε ότι

Υ.Γ : Αν ο φάκελος αποδειχτεί βαρύς, μπορείτε να τον αλλάξετε.

Έστω

το αντιδιαμετρικό σημείο του

στον κύκλο
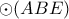
, τότε αρκεί να δείξω ότι
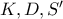
συνευθειακά.
Για αυτό αρκεί ισοδύναμα να δείξω την ισότητα
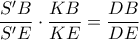
.
Είναι
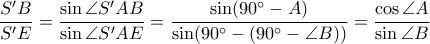
.
Είναι
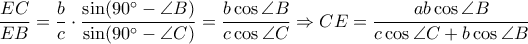
Επίσης
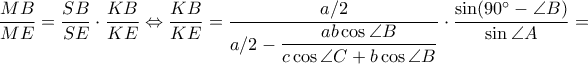
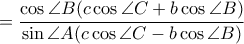
.
Έπειτα
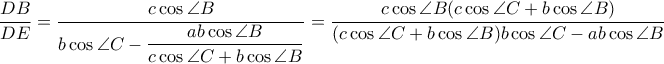
.
Μένει λοιπόν να επαληθεύουμε ότι
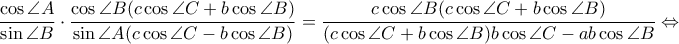
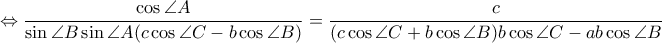
Πολλαπλασιάζουμε με
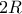
παντού και αυτή γίνεται
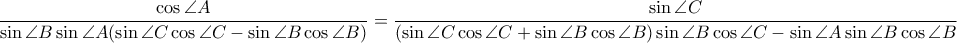
Το
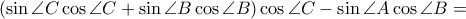

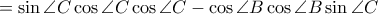
και άρα μένει να δειχθεί ότι
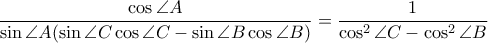
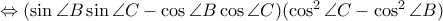
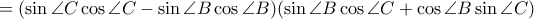
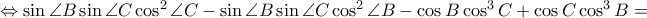
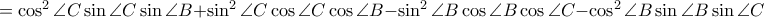
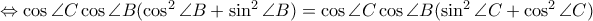
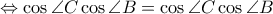
που ισχύει.
 με
με  και περίκεντρο
και περίκεντρο  , ύψος
, ύψος  και
και  το μέσο της πλευράς
το μέσο της πλευράς  . Οι
. Οι  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  και ο περίκυκλος του τριγώνου
και ο περίκυκλος του τριγώνου  επανατέμενει την
επανατέμενει την  στο σημείο
στο σημείο  και την ευθεία
και την ευθεία  στο σημείο
στο σημείο  . Να δείξετε ότι
. Να δείξετε ότι 

 το αντιδιαμετρικό σημείο του
το αντιδιαμετρικό σημείο του 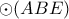 , τότε αρκεί να δείξω ότι
, τότε αρκεί να δείξω ότι 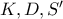 συνευθειακά.
συνευθειακά.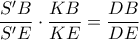 .
.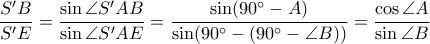 .
.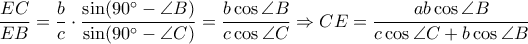
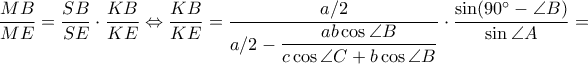
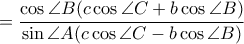 .
.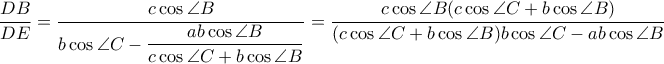 .
.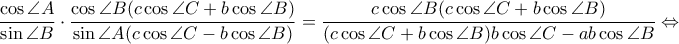
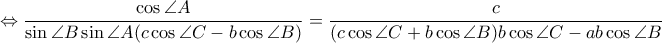
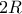 παντού και αυτή γίνεται
παντού και αυτή γίνεται 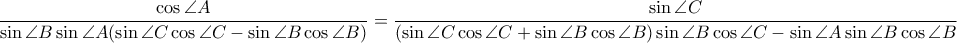
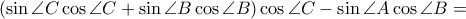

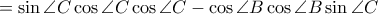
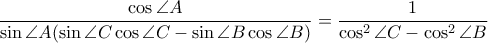
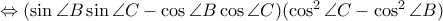
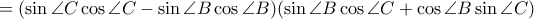
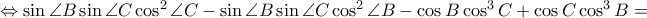
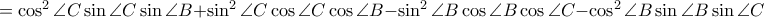
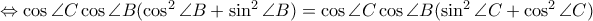
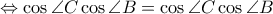 που ισχύει.
που ισχύει.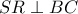 με
με 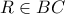 και
και 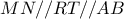 με
με 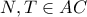
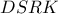 εγγράψιμο οπότε αρκεί
εγγράψιμο οπότε αρκεί 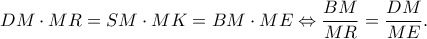
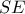 αντιπαράλληλη της
αντιπαράλληλη της  και
και 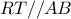 οπότε
οπότε 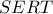 εγγράψιμο , επομένως
εγγράψιμο , επομένως 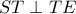
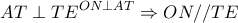 , συνεπώς
, συνεπώς 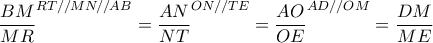 όπως θέλαμε
όπως θέλαμε  το αντιδιαμετρικό του
το αντιδιαμετρικό του  ως προς τον κύκλο
ως προς τον κύκλο  και
και  το σημείο τομής αυτού του κύκλου με την
το σημείο τομής αυτού του κύκλου με την 
 τέμνει την
τέμνει την  Είναι,
Είναι, 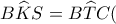 ως παραπληρωματικές της γωνίας
ως παραπληρωματικές της γωνίας 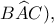 άρα
άρα 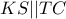
 το
το 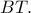 Σύμφωνα όμως με
Σύμφωνα όμως με 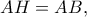 το
το  θα είναι μέσο του
θα είναι μέσο του  και
και 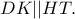 Αλλά,
Αλλά, 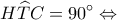
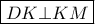
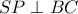 ,
, 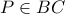 και παίρνω
και παίρνω 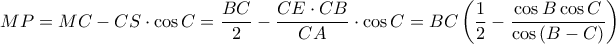
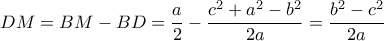 , επομένως
, επομένως 
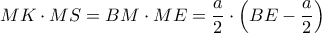 όμως
όμως 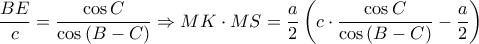
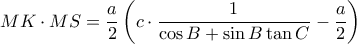
![\displaystyle \tan B\tan C=\frac{4h_{a}^{2}}{4BD\cdot DC}=\frac{4\left [ b^{2}-\left ( \displaystyle \frac{b^{2}-c^{2}+a^{2}}{2a} \right )^{2} \right ]}{\displaystyle \frac{\left ( b^{2}-c^{2}+a^{2} \right )\left ( c^{2}-b^{2}+a^{2} \right )}{a^{2}}}=\frac{4b^{2}-\displaystyle \frac{\left ( b^{2}-c^{2}+a^{2} \right )^{2}}{a^{2}}}{\displaystyle \frac {\left ( b^{2}-c^{2}+a^{2} \right )\left ( c^{2}-b^{2}+a^{2} \right )}{a^{2}}} \displaystyle \tan B\tan C=\frac{4h_{a}^{2}}{4BD\cdot DC}=\frac{4\left [ b^{2}-\left ( \displaystyle \frac{b^{2}-c^{2}+a^{2}}{2a} \right )^{2} \right ]}{\displaystyle \frac{\left ( b^{2}-c^{2}+a^{2} \right )\left ( c^{2}-b^{2}+a^{2} \right )}{a^{2}}}=\frac{4b^{2}-\displaystyle \frac{\left ( b^{2}-c^{2}+a^{2} \right )^{2}}{a^{2}}}{\displaystyle \frac {\left ( b^{2}-c^{2}+a^{2} \right )\left ( c^{2}-b^{2}+a^{2} \right )}{a^{2}}}](/forum/ext/geomar/texintegr/latexrender/pictures/6d3ad51318171c2d5d7c0f7bde66164c.png)
![\displaystyle DM\cdot MP=\frac{b^{2}-c^{2}}{2}\cdot \left [ \frac{1}{2}-\frac{1}{\displaystyle 1+\frac{\displaystyle 4a^{2}b^{2}-\left ( b^{2}-c^{2}+a^{2} \right )^{2}}{\displaystyle \left ( b^{2}-c^{2}+a^{2} \right )\left ( c^{2}-b^{2} +a^{2}\right )}} \right ]=... \displaystyle DM\cdot MP=\frac{b^{2}-c^{2}}{2}\cdot \left [ \frac{1}{2}-\frac{1}{\displaystyle 1+\frac{\displaystyle 4a^{2}b^{2}-\left ( b^{2}-c^{2}+a^{2} \right )^{2}}{\displaystyle \left ( b^{2}-c^{2}+a^{2} \right )\left ( c^{2}-b^{2} +a^{2}\right )}} \right ]=...](/forum/ext/geomar/texintegr/latexrender/pictures/cedc1489a90edd0610920d56bae380f4.png)
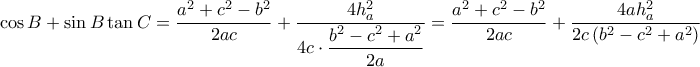
![\displaystyle MK\cdot MS=\frac{a}{2}\left [ c\cdot \frac{1}{\displaystyle \frac{a^{2}+c^{2}-b^{2}}{2ac}+\frac{4a^{2}b^{2}-\left ( b^{2}-c^{2}+a^{2} \right )^{2}}{2ac\left ( b^{2}-c^{2}+a^{2} \right )}}-\frac{a}{2} \right ]=... \displaystyle MK\cdot MS=\frac{a}{2}\left [ c\cdot \frac{1}{\displaystyle \frac{a^{2}+c^{2}-b^{2}}{2ac}+\frac{4a^{2}b^{2}-\left ( b^{2}-c^{2}+a^{2} \right )^{2}}{2ac\left ( b^{2}-c^{2}+a^{2} \right )}}-\frac{a}{2} \right ]=...](/forum/ext/geomar/texintegr/latexrender/pictures/930932529d4491f8d64e5b11c5bf21e4.png)
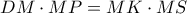 οπότε
οπότε 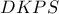 εγγράψιμο και
εγγράψιμο και  κλπ.
κλπ.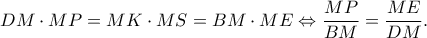
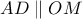 , από Θ. Θαλή είναι
, από Θ. Θαλή είναι 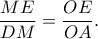 Πλέον αρκεί νδο
Πλέον αρκεί νδο 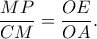
 επανατμήσει τον κύκλο
επανατμήσει τον κύκλο 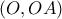 στο σημείο
στο σημείο  , τότε αρκεί νδο
, τότε αρκεί νδο 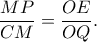
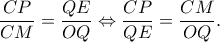
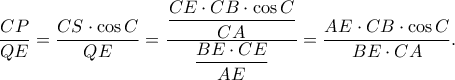

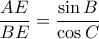 που ισχύει ... κλπ.
που ισχύει ... κλπ.