Ελάχιστη τιμή αθροίσματος κλασμάτων.
Συντονιστές: achilleas, emouroukos, silouan
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Ελάχιστη τιμή αθροίσματος κλασμάτων.
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Σάβ Φεβ 24, 2024 3:15 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: Ελάχιστη τιμή αθροίσματος κλασμάτων.
Με τον μετασχηματισμό 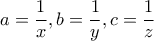 θα αποδείξουμε ότι αν
θα αποδείξουμε ότι αν 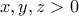 με
με 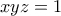 τότε
τότε
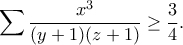
Από την ανισότητα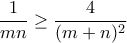 , έχουμε
, έχουμε
![\displaystyle{\sum \frac{x^3}{(y+1)(z+1)} \geq \sum\frac{4x^3}{(2+y+z)^2}\geq \frac{(x+y+z)^3}{[3+x+y+z]^2}} \displaystyle{\sum \frac{x^3}{(y+1)(z+1)} \geq \sum\frac{4x^3}{(2+y+z)^2}\geq \frac{(x+y+z)^3}{[3+x+y+z]^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/93e68ee7b9f527e081c4a07b8d644b49.png) . (*)
. (*)
Οπότε αρκεί να αποδείξουμε ότι
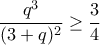 , η οποία ισοδυναμεί με την προφανή
, η οποία ισοδυναμεί με την προφανή 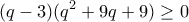 ,
, ![\displaystyle{q=x+y+z\geq 3\sqrt[3]{xyz}=3.} \displaystyle{q=x+y+z\geq 3\sqrt[3]{xyz}=3.}](/forum/ext/geomar/texintegr/latexrender/pictures/a43c47ca697e0dcea0b5553ffc116666.png)
Η (*) είναι άμεση από Hölder.
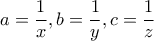 θα αποδείξουμε ότι αν
θα αποδείξουμε ότι αν 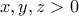 με
με 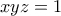 τότε
τότε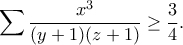
Από την ανισότητα
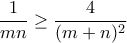 , έχουμε
, έχουμε![\displaystyle{\sum \frac{x^3}{(y+1)(z+1)} \geq \sum\frac{4x^3}{(2+y+z)^2}\geq \frac{(x+y+z)^3}{[3+x+y+z]^2}} \displaystyle{\sum \frac{x^3}{(y+1)(z+1)} \geq \sum\frac{4x^3}{(2+y+z)^2}\geq \frac{(x+y+z)^3}{[3+x+y+z]^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/93e68ee7b9f527e081c4a07b8d644b49.png) . (*)
. (*)Οπότε αρκεί να αποδείξουμε ότι
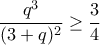 , η οποία ισοδυναμεί με την προφανή
, η οποία ισοδυναμεί με την προφανή 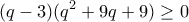 ,
, ![\displaystyle{q=x+y+z\geq 3\sqrt[3]{xyz}=3.} \displaystyle{q=x+y+z\geq 3\sqrt[3]{xyz}=3.}](/forum/ext/geomar/texintegr/latexrender/pictures/a43c47ca697e0dcea0b5553ffc116666.png)
Η (*) είναι άμεση από Hölder.
Μάγκος Θάνος
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Ελάχιστη τιμή αθροίσματος κλασμάτων.
Θα δείξουμε ότι η ελάχιστη τιμή είναι 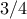 που λαμβάνεται όταν
που λαμβάνεται όταν  .
.
Μπορούμε να βρούμε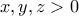 ώστε
ώστε 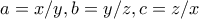 . Τότε
. Τότε
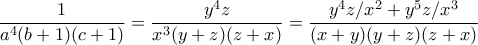
Αρκεί να δείξουμε ότι
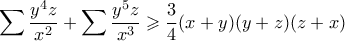
Από ΑΜ-ΓΜ έχουμε
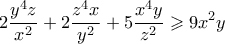
και προσθέτοντας κυκλικά παίρνουμε
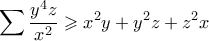
Πάλι από ΑΜ-ΓΜ έχουμε
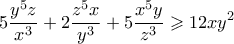
και προσθέτοντας κυκλικά παίρνουμε
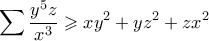
Συνολικά παίρνουμε
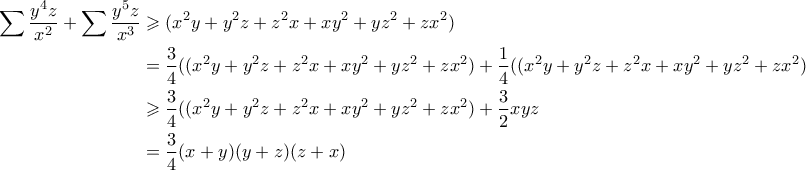
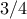 που λαμβάνεται όταν
που λαμβάνεται όταν  .
.Μπορούμε να βρούμε
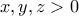 ώστε
ώστε 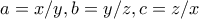 . Τότε
. Τότε 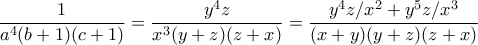
Αρκεί να δείξουμε ότι
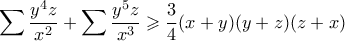
Από ΑΜ-ΓΜ έχουμε
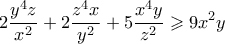
και προσθέτοντας κυκλικά παίρνουμε
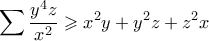
Πάλι από ΑΜ-ΓΜ έχουμε
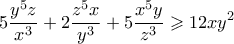
και προσθέτοντας κυκλικά παίρνουμε
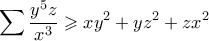
Συνολικά παίρνουμε
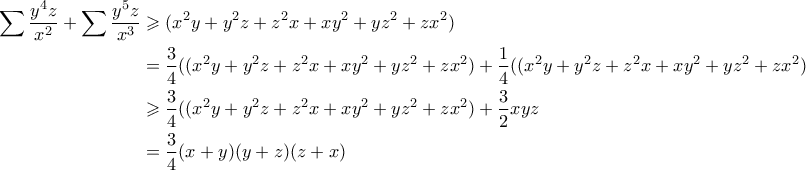
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
