 θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:
θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:![\displaystyle{\frac{16}{27} \left ( \frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} \right )^3 + \sqrt[3]{\frac{abc}{\left ( a+b \right )\left ( b+c \right )\left ( c+a \right )}} \geq \frac{5}{2}} \displaystyle{\frac{16}{27} \left ( \frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} \right )^3 + \sqrt[3]{\frac{abc}{\left ( a+b \right )\left ( b+c \right )\left ( c+a \right )}} \geq \frac{5}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/ce9df23c0636388ae75a14866878d594.png)
Συντονιστές: achilleas, emouroukos, silouan
Μη αναγνωσμένη δημοσίευση από Tolaso J Kos » Τετ Μαρ 22, 2023 8:39 am
 θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:
θετικοί πραγματικοί αριθμοί. Να δειχθεί ότι:![\displaystyle{\frac{16}{27} \left ( \frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} \right )^3 + \sqrt[3]{\frac{abc}{\left ( a+b \right )\left ( b+c \right )\left ( c+a \right )}} \geq \frac{5}{2}} \displaystyle{\frac{16}{27} \left ( \frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} \right )^3 + \sqrt[3]{\frac{abc}{\left ( a+b \right )\left ( b+c \right )\left ( c+a \right )}} \geq \frac{5}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/ce9df23c0636388ae75a14866878d594.png)

Μη αναγνωσμένη δημοσίευση από Manolis Petrakis » Τετ Μαρ 22, 2023 2:55 pm
Κατ' αρχάς από την ανισότητα Nesbitt:
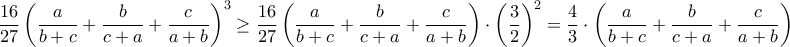
![\dfrac{1}{8}\geq\dfrac{abc}{(a+b)(b+c)(c+a)}\Rightarrow \sqrt[3]{\dfrac{abc}{(a+b)(b+c)(c+a)}}\geq \dfrac{4abc}{(a+b)(b+c)(c+a)} \dfrac{1}{8}\geq\dfrac{abc}{(a+b)(b+c)(c+a)}\Rightarrow \sqrt[3]{\dfrac{abc}{(a+b)(b+c)(c+a)}}\geq \dfrac{4abc}{(a+b)(b+c)(c+a)}](/forum/ext/geomar/texintegr/latexrender/pictures/eda08dde3f5f8bd84311e0aa5641666e.png)
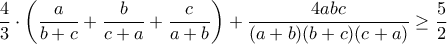
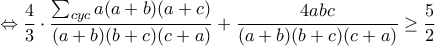
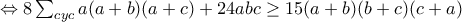
![\Leftrightarrow 8(a^3+b^3+c^3) +18abc\geq 7[ab(a+b)+bc(b+c)+ca(c+a)] \Leftrightarrow 8(a^3+b^3+c^3) +18abc\geq 7[ab(a+b)+bc(b+c)+ca(c+a)]](/forum/ext/geomar/texintegr/latexrender/pictures/54e248236e6e57e04b252314ffff0ae0.png)
![7(a^3+b^3+c^3+3abc)\geq 7[ab(a+b)+bc(b+c)+ca(c+a)]\ (Schur) 7(a^3+b^3+c^3+3abc)\geq 7[ab(a+b)+bc(b+c)+ca(c+a)]\ (Schur)](/forum/ext/geomar/texintegr/latexrender/pictures/d5f4ef9c36bf8debef27570a5a55498a.png)
Επιστροφή σε “Άλγεβρα - Επίπεδο Αρχιμήδη (Seniors)”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off