 , του τεταρτοκυκλίου
, του τεταρτοκυκλίου  , κατά τμήμα :
, κατά τμήμα :  και
και φέρω το εφαπτόμενο τμήμα
 , το οποίο τέμνει την προέκταση της
, το οποίο τέμνει την προέκταση της  στο σημείο
στο σημείο  .
.Υπολογίστε το τμήμα
 ( συναρτήσει της ακτίνας
( συναρτήσει της ακτίνας 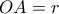 ) και την
) και την  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , του τεταρτοκυκλίου
, του τεταρτοκυκλίου  , κατά τμήμα :
, κατά τμήμα :  και
και  , το οποίο τέμνει την προέκταση της
, το οποίο τέμνει την προέκταση της  στο σημείο
στο σημείο  .
. ( συναρτήσει της ακτίνας
( συναρτήσει της ακτίνας 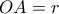 ) και την
) και την  .
.Αν η εφαπτόμενη στο
 τέμνει την
τέμνει την  sto
sto  ,θα είναι
,θα είναι  και λόγω ισότητας των τριγώνων
και λόγω ισότητας των τριγώνων είναι και
είναι και  άρα
άρα  οπότε
οπότε 
 άρα
άρα 
 )
)
Ας είναι
 το αντιδιαμετρικό του
το αντιδιαμετρικό του  και
και  η προβολή του
η προβολή του  στην ευθεία
στην ευθεία  . Άμεσες συνέπειες :
. Άμεσες συνέπειες :  .
. είναι εγγράψιμο με ίσες διαγωνίους δηλαδή ισοσκελές τραπέζιο.
Θέτω
είναι εγγράψιμο με ίσες διαγωνίους δηλαδή ισοσκελές τραπέζιο.
Θέτω  , θα έχω:
, θα έχω:  . Το Π. Θ. στο
. Το Π. Θ. στο  και λόγω της
και λόγω της  δίδει:
δίδει:  .
.
Είναι
 και
και  Εξάλλου με Π.Θ προκύπτει
Εξάλλου με Π.Θ προκύπτει  Με νόμο συνημιτόνου στο
Με νόμο συνημιτόνου στο 

 κι επειδή είναι οξείες,
κι επειδή είναι οξείες, 


 και
και 
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 8 επισκέπτες