 το κέντρο ημικυκλίου διαμέτρου
το κέντρο ημικυκλίου διαμέτρου  . Ας είναι
. Ας είναι  εσωτερικό σημείο της ακτίνας
εσωτερικό σημείο της ακτίνας  .
.Θεωρούμε την ευθεία
 , κάθετη στην
, κάθετη στην  στο
στο  . Σημείο
. Σημείο  κινείται επί του ημικυκλίου . Οι
κινείται επί του ημικυκλίου . Οι  τέμνουν την
τέμνουν την  στα
στα  α) Δείξετε ότι οι ευθείες ,
α) Δείξετε ότι οι ευθείες , τέμνονται σε σημείο , έστω
τέμνονται σε σημείο , έστω  , πάνω στο ημικύκλιο.
, πάνω στο ημικύκλιο. β) Αν το
 σταθερό και το
σταθερό και το  μεταβλητό , δείξετε ότι η ευθεία
μεταβλητό , δείξετε ότι η ευθεία  διέρχεται από σταθερό σημείο , έστω
διέρχεται από σταθερό σημείο , έστω  , επί πλέον δε
, επί πλέον δε γ) δείξετε ότι τα εφαπτόμενα τμήματα,
 προς τον κύκλο
προς τον κύκλο  , έχουν σταθερό μήκος το καθένα.
, έχουν σταθερό μήκος το καθένα.δ) Να βρείτε πως θα επιλέξουμε το σταθερό
 πάνω στην
πάνω στην  , ώστε
, ώστε  .
.
 είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  Άρα η
Άρα η  θα τέμνει την
θα τέμνει την  σε σημείο
σε σημείο  στο
στο 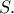 Θέτω
Θέτω  την ακτίνα του ημικυκλίου, το σταθερό τμήμα
την ακτίνα του ημικυκλίου, το σταθερό τμήμα  και
και 
 στο
στο 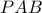 και Μενέλαο στο ίδιο τρίγωνο με διατέμνουσα
και Μενέλαο στο ίδιο τρίγωνο με διατέμνουσα  παίρνω διαδοχικά:
παίρνω διαδοχικά:
 που είναι σταθερό.
που είναι σταθερό.








 σταθερό .Επειδή
σταθερό .Επειδή  θα είναι
θα είναι  .
. άρα
άρα  συνευθειακά
συνευθειακά του τριγώνου
του τριγώνου  θα είναι
θα είναι 

 είναι ο κύκλος Euler του τριγώνου
είναι ο κύκλος Euler του τριγώνου  απ όπου
απ όπου 
 και
και 