ΑνΧΡΗΣΤΟΣ ΡΑΠΤΗΣ έγραψε:Γεια σας και απο εμενα. Παρακολουθω μερες τωρα την προσπαθεια σας αλλα δεν μπορουσα να συμμετεχω λογω υποχρεωσεων. Θα ηθελα κι εγω να στειλω καποιες λυσεις ομως δεν το εχω με την LaTex. Θα μπορουσα να στειλω σε καποιον αρχειο .docx ή (περισσοτερο ευκολο για μενα) σκαναρισμενο χειρογραφο.
Και μια βοηθεια για οποιον εχει λιγο χρονο : Εχω κολλησει στην 3708 στο (β) ερωτημα. Οποιος μπορει ας στειλει μια υποδειξη (ή και λυση...)
Υ.Γ. : Οι 3708 και 3709 ειναι ιδιες. Επισης στην 3711 το ερωτημα α.iii. θα επρεπε να προηγειται του α.ii.
 είναι το μέσο του
είναι το μέσο του  και
και  το μέσο του
το μέσο του  , τότε το
, τότε το 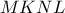 είναι ορθογώνιο. Άρα
είναι ορθογώνιο. Άρα 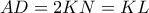 , διότι το τρίγωνο
, διότι το τρίγωνο 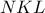 είναι ορθογώνιο.
είναι ορθογώνιο.Βλέπω και άλλη λύση, αλλά για την ώρα καλή είναι και αυτή . Νομίζω επίσης ότι το μέσο Μ μπορούμε και να μην το πάρουμε. Μας αρκεί που το τρίγωνο
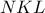 είναι ορθογώνιο και ότι η γωνία
είναι ορθογώνιο και ότι η γωνία 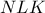 είναι ίση με την γωνία
είναι ίση με την γωνία 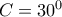
Μπάμπης

 , είναι
, είναι 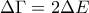 .
. ισχύουν:
ισχύουν: 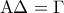 ,
, 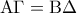 , και
, και 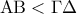 .
. και
και 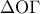 είναι ισοσκελή. (Μονάδες 8)
είναι ισοσκελή. (Μονάδες 8) 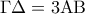 και
και  τα μέσα των διαγωνίων
τα μέσα των διαγωνίων 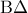 και
και  αντίστοιχα, να αποδείξετε ότι το τετράπλευρο
αντίστοιχα, να αποδείξετε ότι το τετράπλευρο 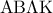 είναι ορθογώνιο παραλληλόγραμμο. (Μονάδες 9)
είναι ορθογώνιο παραλληλόγραμμο. (Μονάδες 9)
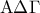 και
και 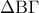 είναι ίσα μεταξύ τους καθώς έχουν τρείς πλευρές ίσες. Τις
είναι ίσα μεταξύ τους καθώς έχουν τρείς πλευρές ίσες. Τις 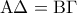 ,
,  κοινή.
κοινή. 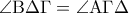 , άρα το τρίγωνο
, άρα το τρίγωνο 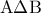 και
και  είναι ίσα μεταξύ τους καθώς έχουν τρείς πλευρές ίσες. Τις
είναι ίσα μεταξύ τους καθώς έχουν τρείς πλευρές ίσες. Τις 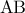
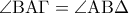 , άρα το τρίγωνο
, άρα το τρίγωνο 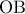 είναι ισοσκελές.
είναι ισοσκελές.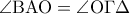 το οποίο σημαίνει ότι οι εντός εναλλάξ γωνίες που σχηματίζονται είναι ίσες άρα
το οποίο σημαίνει ότι οι εντός εναλλάξ γωνίες που σχηματίζονται είναι ίσες άρα 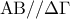 και το τετράπλευρο είναι τραπέζιο.
και το τετράπλευρο είναι τραπέζιο.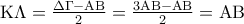
 διαπιστώνουμε ότι είναι ίσα καθώς
διαπιστώνουμε ότι είναι ίσα καθώς 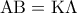 ,
,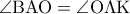
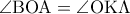 ως εντός εναλλάξ, είναι ισοσκελή άρα οι διαγώνιοι του παραλληλογράμμου είναι ίσες συνεπώς το παραλληλόγραμμο είναι ορθογώνιο.
ως εντός εναλλάξ, είναι ισοσκελή άρα οι διαγώνιοι του παραλληλογράμμου είναι ίσες συνεπώς το παραλληλόγραμμο είναι ορθογώνιο.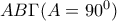 και
και 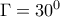 με
με  τα μέσα των πλευρών
τα μέσα των πλευρών  και
και  στο σημείο
στο σημείο  .
. είναι διχοτόμος της γωνίας Β. (Μονάδες
είναι διχοτόμος της γωνίας Β. (Μονάδες  )
)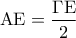 (Μονάδες
(Μονάδες  . (Μονάδες
. (Μονάδες  )
) είναι το ύψος του τριγώνου
είναι το ύψος του τριγώνου  που τέμνει τη
που τέμνει τη  , να αποδείξετε ότι τα σημεία
, να αποδείξετε ότι τα σημεία 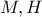 και
και 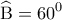 . Το τρίγωνο
. Το τρίγωνο  είναι ισοσκελές επειδή η
είναι ισοσκελές επειδή η 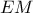 είναι μεσοκάθετος της
είναι μεσοκάθετος της 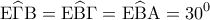
 θα ισαπέχει από τις πλευρές της, οπότε:
θα ισαπέχει από τις πλευρές της, οπότε: 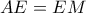 .
.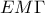 έχουμε:
έχουμε: 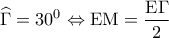 .
.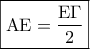
 (η διάμεσος
(η διάμεσος  , η
, η .
.  είναι ύψη του τριγώνου
είναι ύψη του τριγώνου είναι το τρίτο ύψος του τριγώνου.
είναι το τρίτο ύψος του τριγώνου.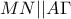 (ενώνει τα μέσα των πλευρών του τριγώνου) κι επειδή
(ενώνει τα μέσα των πλευρών του τριγώνου) κι επειδή 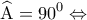
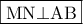
 ενός κύκλου φέρνουμε τα εφαπτόμενα τμήματα
ενός κύκλου φέρνουμε τα εφαπτόμενα τμήματα 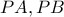 και τη διακεντρική ευθεία
και τη διακεντρική ευθεία 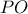 που τέμνει τον κύκλο στα
που τέμνει τον κύκλο στα 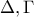 αντίστοιχα.Η εφαπτομένη του κύκλου στο
αντίστοιχα.Η εφαπτομένη του κύκλου στο  τέμνει τις προεκτάσεις των
τέμνει τις προεκτάσεις των 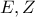 αντίστοιχα.
αντίστοιχα.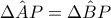
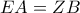
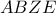 είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.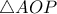 και
και 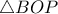 .
. ως εφαπτόμενα τμήματα και
ως εφαπτόμενα τμήματα και 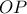 κοινή άρα είναι ίσα.Επομένως
κοινή άρα είναι ίσα.Επομένως 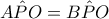 .
.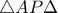 και
και 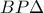 .Αυτά έχουν
.Αυτά έχουν 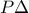 κοινή και όπως δείξαμε στην προηγούμενη σύγκριση
κοινή και όπως δείξαμε στην προηγούμενη σύγκριση 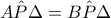 επομένως από Π-Γ-Π είναι ίσα κι έτσι
επομένως από Π-Γ-Π είναι ίσα κι έτσι 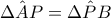 .
.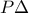 που περνά και από τα
που περνά και από τα 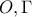 είναι κάθετη στην
είναι κάθετη στην  επειδή η τελευταία είναι εφαπτόμενη του κύκλου στο
επειδή η τελευταία είναι εφαπτόμενη του κύκλου στο 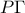 ταυτίζεται με την ακτίνα
ταυτίζεται με την ακτίνα 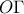 στο τμήμα αυτό.
στο τμήμα αυτό.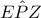 όπως δείξαμε παραπάνω άρα το τρίγωνο
όπως δείξαμε παραπάνω άρα το τρίγωνο 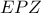 είναι ισοσκελές κι έτσι
είναι ισοσκελές κι έτσι 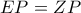 .Αφαιρώντας κατά μέλη με την
.Αφαιρώντας κατά μέλη με την 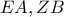 δεν είναι παράλληλες αφού τέμνονται στο
δεν είναι παράλληλες αφού τέμνονται στο 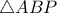 και
και 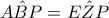 κι επειδή αυτές οι δύο είναι εντός-εκτός και επί τα αυτά,οι ευθείες
κι επειδή αυτές οι δύο είναι εντός-εκτός και επί τα αυτά,οι ευθείες 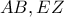 θα είναι παράλληλες.
θα είναι παράλληλες. με
με 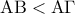 και η διχοτόμος
και η διχοτόμος 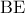 της γωνίας
της γωνίας  .
.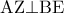 όπου
όπου 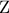 σημείο της
σημείο της 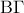 και
και 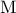 το μέσον της
το μέσον της 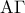 , να αποδείξετε ότι :
, να αποδείξετε ότι : 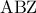 είναι ισοσκελές . (Μονάδες 7)
είναι ισοσκελές . (Μονάδες 7) 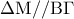 και
και 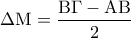 (Μονάδες 10)
(Μονάδες 10) 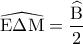 όπου
όπου 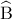 η γωνία του τριγώνου
η γωνία του τριγώνου 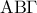 . (Μονάδες 8)
. (Μονάδες 8)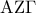 τα
τα 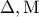 είναι τα μέσα δυο πλευρών , οπότε
είναι τα μέσα δυο πλευρών , οπότε 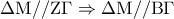 .
.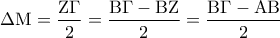 , αφού από το (α) ισχύει
, αφού από το (α) ισχύει 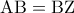 .
.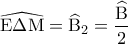 , ως εντός εκτός και επί τα αυτά μέρη των παραλλήλων
, ως εντός εκτός και επί τα αυτά μέρη των παραλλήλων  , τεμνομένων υπό της
, τεμνομένων υπό της 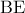 !!
!! η διχοτόμος
η διχοτόμος 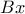 της γωνίας
της γωνίας 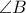 και η διχοτόμος
και η διχοτόμος 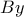 της εξωτερικής γωνίας
της εξωτερικής γωνίας 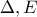 οι προβολές της κορυφής
οι προβολές της κορυφής  στις
στις 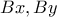 αντίστοιχα,να αποδειχθεί ότι:
αντίστοιχα,να αποδειχθεί ότι: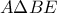 είναι ορθογώνιο,
είναι ορθογώνιο,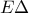 είναι παράλληλη προς τη
είναι παράλληλη προς τη  και διέρχεται από το μέσο
και διέρχεται από το μέσο  της
της 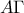 ,
,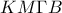 είναι τραπέζιο του οποίου η διάμεσος ισούται με
είναι τραπέζιο του οποίου η διάμεσος ισούται με 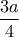 όπου
όπου 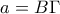 .
. 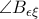 είναι εφεξής και παραπληρωματικές άρα οι διχοτόμοι τους σχηματίζουν ορθή γωνία.Ακόμη
είναι εφεξής και παραπληρωματικές άρα οι διχοτόμοι τους σχηματίζουν ορθή γωνία.Ακόμη 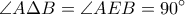 επειδή οι
επειδή οι 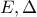 είναι προβολές του σημείου
είναι προβολές του σημείου 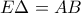 ως διαγώνιοι ορθογωνίου.Ξέρουμε πως αυτές διχοτομούνται άρα
ως διαγώνιοι ορθογωνίου.Ξέρουμε πως αυτές διχοτομούνται άρα 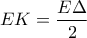 και
και 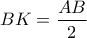 άρα
άρα 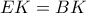 κι έτσι το τρίγωνο
κι έτσι το τρίγωνο 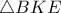 είναι ισοσκελές.
είναι ισοσκελές.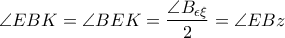 .
.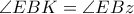 κι επειδή οι γωνίες αυτές είναι εντός εναλλάξ των ευθειών
κι επειδή οι γωνίες αυτές είναι εντός εναλλάξ των ευθειών 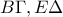 άρα
άρα 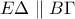 .
. αφού τα δύο αυτά τμήματα είναι διαγώνιοι παραλληλογράμμου..
αφού τα δύο αυτά τμήματα είναι διαγώνιοι παραλληλογράμμου..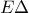 είναι παράλληλη μίας πλευράς λοιπόν που περνά από το μέσο της άλλης άρα θα περνά από το μέσο και της τρίτης πλευράς το οποίο είναι το σημείο
είναι παράλληλη μίας πλευράς λοιπόν που περνά από το μέσο της άλλης άρα θα περνά από το μέσο και της τρίτης πλευράς το οποίο είναι το σημείο 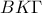 δεν είναι παράλληλες αφού τέμνονται στο
δεν είναι παράλληλες αφού τέμνονται στο 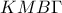 είναι τραπέζιο.Η διάμεσός του είναι ίση με
είναι τραπέζιο.Η διάμεσός του είναι ίση με 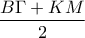 .Όμως η
.Όμως η  συνδέει μέσα πλευρών άρα θα είναι ίση με
συνδέει μέσα πλευρών άρα θα είναι ίση με 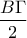 .
.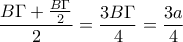 όπως θέλαμε.
όπως θέλαμε. δίνονται σημεία
δίνονται σημεία  στις πλευρές
στις πλευρές 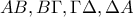 ώστε
ώστε 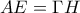 και
και 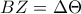 .
.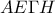 είναι παραλληλόγραμμο,
είναι παραλληλόγραμμο,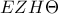 είναι παραλληλόγραμμο,
είναι παραλληλόγραμμο,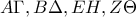 διέρχονται από το ίδιο σημείο.
διέρχονται από το ίδιο σημείο.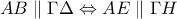 αφού τα σημεία
αφού τα σημεία 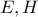 βρίσκονται πάνω στα τμήματα
βρίσκονται πάνω στα τμήματα 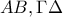 .
.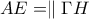 κι έτσι το τετράπλευρο
κι έτσι το τετράπλευρο 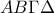 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.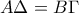 και
και 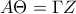 .
.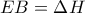 .
.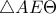 και
και 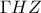 έχουν
έχουν 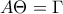 και
και 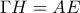 .
.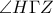 και
και 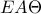 είναι ίσες ως απέναντι παραλληλογράμμου.Επομένως τα δύο τρίγωνα αυτά είναι ίσα από Π-Γ-Π.Ομοίως είναι ίσα τα τρίγωνα
είναι ίσες ως απέναντι παραλληλογράμμου.Επομένως τα δύο τρίγωνα αυτά είναι ίσα από Π-Γ-Π.Ομοίως είναι ίσα τα τρίγωνα 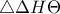 και
και 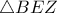 .Από τις δύο αυτές ισότητες λαμβάνουμε
.Από τις δύο αυτές ισότητες λαμβάνουμε 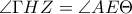 και
και 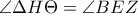 .
.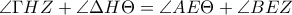 .Όμως
.Όμως 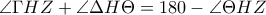 και
και 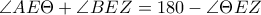 .Επομένως
.Επομένως 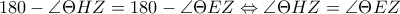 .
.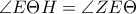 .Άρα οι απέναντι γωνίες του τετραπλεύρου
.Άρα οι απέναντι γωνίες του τετραπλεύρου  περνά από το μέσο της
περνά από το μέσο της 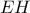 περνά από το μέσο της
περνά από το μέσο της 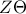 περνά από το μέσο της
περνά από το μέσο της 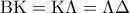 .
. 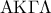 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. 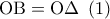
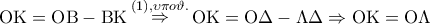
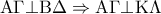
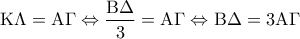
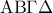 και έστω
και έστω  το σημείο τομής των διαγωνίων
το σημείο τομής των διαγωνίων 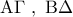 .
.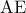 κάθετη στη διαγώνιο
κάθετη στη διαγώνιο 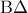 . Εάν
. Εάν 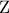 είναι το συμμετρικό του
είναι το συμμετρικό του 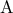 ως προς τη διαγώνιο ΒΔ
ως προς τη διαγώνιο ΒΔ 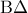 , τότε να αποδείξετε ότι:
, τότε να αποδείξετε ότι: 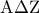 είναι ισοσκελές . (Μονάδες 7)
είναι ισοσκελές . (Μονάδες 7) 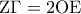 . (Μονάδες 9)
. (Μονάδες 9) 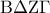 είναι ισοσκελές τραπέζιο. (Μονάδες 9)
είναι ισοσκελές τραπέζιο. (Μονάδες 9)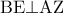 , και το
, και το 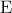 είναι μέσον της
είναι μέσον της 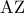 , η
, η 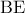 είναι μεσοκάθετη της
είναι μεσοκάθετη της 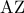 κι αφού το
κι αφού το 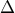 είναι σημείο της μεσοκαθέτου , έχουμε
είναι σημείο της μεσοκαθέτου , έχουμε 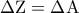 άρα το
άρα το 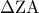 είναι ισοσκελές
είναι ισοσκελές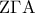 τα
τα 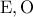 είναι μέσα δυο πλευρών (το
είναι μέσα δυο πλευρών (το 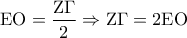 .
.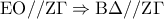 άρα το
άρα το 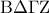 είναι τραπέζιο .
είναι τραπέζιο .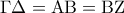 αφού το
αφού το 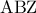 είναι ισοσκελές . Άρα είναι ισοσκελές τραπέζιο .
είναι ισοσκελές . Άρα είναι ισοσκελές τραπέζιο .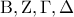 είναι ισοσκελές τραπέζιο , διότι ανάλογα με την κατασκευή του σχήματος , αλλάζει η διάταξη των γραμμάτων .
είναι ισοσκελές τραπέζιο , διότι ανάλογα με την κατασκευή του σχήματος , αλλάζει η διάταξη των γραμμάτων .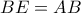 και στην προέκταση της
και στην προέκταση της 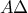 παίρνουμε τμήμα
παίρνουμε τμήμα 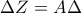 .
.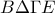 και
και 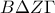 είναι παραλληλόγραμμα.
είναι παραλληλόγραμμα.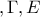 είναι συνευθειακά.
είναι συνευθειακά.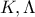 τα μέσα των
τα μέσα των 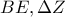 αντίστοιχα τότε να αποδειχθεί ότι
αντίστοιχα τότε να αποδειχθεί ότι 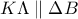 και
και 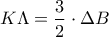 .
.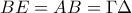 από το παραλληλόγραμμο
από το παραλληλόγραμμο 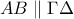 κι επειδή το
κι επειδή το  βρίσκεται στην ευθεία
βρίσκεται στην ευθεία 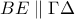 .Άρα
.Άρα 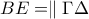 κι έτσι το τετράπλευρο
κι έτσι το τετράπλευρο 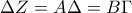 από το
από το 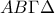 που είναι παραλληλόγραμμο.Ακόμη
που είναι παραλληλόγραμμο.Ακόμη 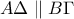 κι επειδή το
κι επειδή το  βρίσκεται στην ευθεία
βρίσκεται στην ευθεία 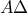 θα είναι
θα είναι 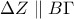 .Τελικά
.Τελικά 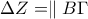 άρα το τετράπλευρο
άρα το τετράπλευρο 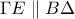 και
και 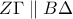 .Από το
.Από το  και
και 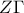 ανήκουν στην ίδια ευθεία.Έτσι τα σημεία
ανήκουν στην ίδια ευθεία.Έτσι τα σημεία 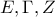 είναι συνευθειακά.
είναι συνευθειακά.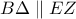 και οι ευθείες
και οι ευθείες 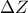 και
και  δεν είναι παράλληλες αφού τέμνονται στο
δεν είναι παράλληλες αφού τέμνονται στο 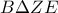 είναι τραπέζιο.Η
είναι τραπέζιο.Η  είναι διάμεσός του.Έτσι ισούται
είναι διάμεσός του.Έτσι ισούται 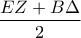 .Όμως
.Όμως 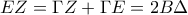 .Επομένως
.Επομένως 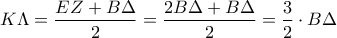 όπως θέλαμε.
όπως θέλαμε.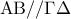 θα είναι
θα είναι 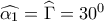 .
.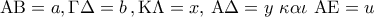 .
.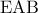 επειδή η κάθετη πλευρά
επειδή η κάθετη πλευρά  βρίσκεται απέναντι των
βρίσκεται απέναντι των 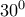 θα είναι ίση με το μισό της υποτείνουσας , δηλαδή
θα είναι ίση με το μισό της υποτείνουσας , δηλαδή 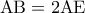 ή
ή 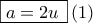 .
.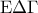 προκύπτει :
προκύπτει : 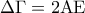 ή
ή 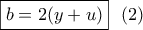 . Από τις (1) και
. Από τις (1) και  έχουμε :
έχουμε : 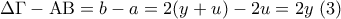 .
. 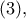
 .
.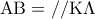 και άρα
και άρα 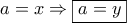 ( λόγω του β ερωτήματος) . Μα τότε το τρίγωνο
( λόγω του β ερωτήματος) . Μα τότε το τρίγωνο  και άρα
και άρα 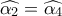 . Όμως
. Όμως 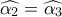 ως εντός εναλλάξ των παραλλήλων
ως εντός εναλλάξ των παραλλήλων 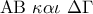 που τέμνονται από την
που τέμνονται από την  . Έτσι και λόγω μεταβατικότητας
. Έτσι και λόγω μεταβατικότητας 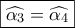 . Δηλαδή η
. Δηλαδή η 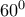 του
του  και ακτίνας
και ακτίνας  . Από τυχαίο σημείο
. Από τυχαίο σημείο  του
του 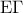 φέρνουμε παράλληλη
φέρνουμε παράλληλη  στο
στο  .
. με
με 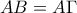 και το ύψος του
και το ύψος του  .Φέρνουμε
.Φέρνουμε 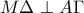 και θεωρούμε το μέσο
και θεωρούμε το μέσο  του
του 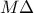 .Από το
.Από το 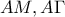 στα
στα 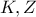 αντίστοιχα.
αντίστοιχα.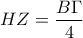 ,
,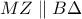 ,
, είναι κάθετη στη
είναι κάθετη στη 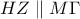 κι επειδή το
κι επειδή το  και
και 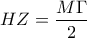 .
.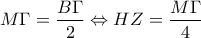 .
.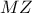 περνά από τα μέσα των
περνά από τα μέσα των 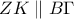 και
και 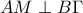 θα είναι
θα είναι 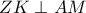 .Επομένως το
.Επομένως το 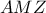 κι έτσι
κι έτσι 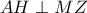 .
.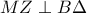 άρα
άρα 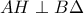 .
. για την οποία ισχύει
για την οποία ισχύει 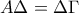 . Η
. Η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας 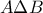 και η
και η  είναι παράλληλη στην
είναι παράλληλη στην 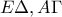 είναι παράλληλα. (Μονάδες
είναι παράλληλα. (Μονάδες  )
)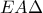 είναι ισοσκελές. (Μονάδες
είναι ισοσκελές. (Μονάδες  )
)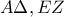 διχοτομούνται. (Μονάδες
διχοτομούνται. (Μονάδες 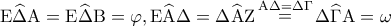
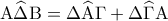 (ως εξωτερική στο τρίγωνο
(ως εξωτερική στο τρίγωνο 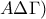
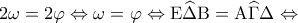
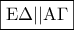 (επειδή οι εντός εκτός και επί τα αυτά μέρη γωνίες είναι ίσες)
(επειδή οι εντός εκτός και επί τα αυτά μέρη γωνίες είναι ίσες)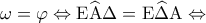
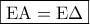 και το τρίγωνο
και το τρίγωνο 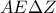 είναι παραλληλόγραμμο, οπότε τα τμήματα
είναι παραλληλόγραμμο, οπότε τα τμήματα 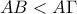 .Στην προέκταση της
.Στην προέκταση της  παίρνουμε σημείο
παίρνουμε σημείο 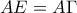 .Στην πλευρά
.Στην πλευρά 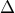 ώστε
ώστε 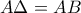 .Αν τα τμήματα
.Αν τα τμήματα 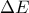 και
και  και προέκταση της
και προέκταση της  τέμνει την
τέμνει την  στο
στο 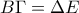 ,
, ,
,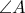 ,
,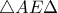 και
και 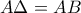 (από υπόθεση).Ακόμη έχουν κοινή τη γωνία
(από υπόθεση).Ακόμη έχουν κοινή τη γωνία 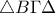 και
και 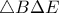 .Έχουν κοινή την
.Έχουν κοινή την 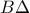 και
και 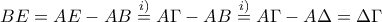 .Επομένως από Π-Π-Π τα τρίγωνα είναι ίσα κι έτσι
.Επομένως από Π-Π-Π τα τρίγωνα είναι ίσα κι έτσι 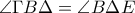 .Επομένως το τρίγωνο
.Επομένως το τρίγωνο 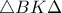 είναι ισοσκελές κι έτσι
είναι ισοσκελές κι έτσι 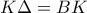 .
.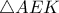 και
και 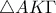 .Έχουν κοινή την
.Έχουν κοινή την 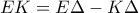 .Όμως
.Όμως 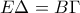 και
και 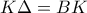 οπότε
οπότε 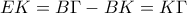 .Τελικά από Π-Π-Π τα δύο τρίγωνα είναι ίσα κι έτσι
.Τελικά από Π-Π-Π τα δύο τρίγωνα είναι ίσα κι έτσι 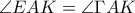 ή ισοδύναμα η
ή ισοδύναμα η 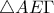 είναι ισοσκελές και η
είναι ισοσκελές και η 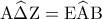 ( εντός εκτός και επί τα αυτά μέρη των
( εντός εκτός και επί τα αυτά μέρη των 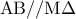 που τέμνονται από την
που τέμνονται από την  » θεωρεί κακώς τα σημεία
» θεωρεί κακώς τα σημεία 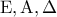 συνευθειακά γιατί αυτό είναι ζητούμενο και συνεπώς αυτό είναι το σημείο στο οποίο εστιάζεται το λάθος .
συνευθειακά γιατί αυτό είναι ζητούμενο και συνεπώς αυτό είναι το σημείο στο οποίο εστιάζεται το λάθος . και ακτίνα
και ακτίνα 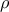 . Έστω σημείο
. Έστω σημείο 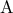 εξωτερικό του κύκλου και τα εφαπτόμενα τμήματα
εξωτερικό του κύκλου και τα εφαπτόμενα τμήματα 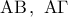 ώστε να ισχύει
ώστε να ισχύει 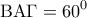 . Έστω ότι η εφαπτόμενη του κύκλου στο
. Έστω ότι η εφαπτόμενη του κύκλου στο 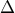 τέμνει τις
τέμνει τις 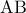 και
και 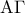 στα
στα 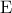 και
και  αντίστοιχα.
αντίστοιχα. 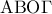 είναι εγγράψιμο με
είναι εγγράψιμο με 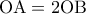 . (Μονάδες 6)
. (Μονάδες 6) 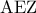 είναι ισόπλευρο. (Μονάδες 6)
είναι ισόπλευρο. (Μονάδες 6) 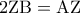 (Μονάδες 7)
(Μονάδες 7) 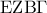 είναι ισοσκελές τραπέζιο. (Μονάδες 6)
είναι ισοσκελές τραπέζιο. (Μονάδες 6)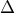 ;
;