Σωτήρη, απλά, όμορφα και γεωματρικά. Ευχαριστώ πολύ.
Βάζω και την δική μου προσέγγιση:
Ξεκινώ από το

και παίρνω τυχόντα σημεία

και

της έλλειψης.
Θα αδιαφορήσω για την συνθήκη
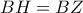
και θα βρω τις συνθήκες για τα
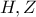
ώστε το εμβαδόν του

να είναι το μέγιστο δυνατό. Αν για αυτές τις τιμές ισχύει επιπλέον ότι

τότε τελείωσα. Το εμβαδόν του τριγώνου ισούται με

Αυτό το υπολόγισα με τον τύπο που λέει ότι δοθέντων

στο επίπεδο, το εμβαδόν του τριγώνου

ισούται με το μισό της απόλυτης τιμής της ορίζουσας του πίνακα

[Όπως με ενημέρωσαν ο τύπος αυτός είναι γνωστός στους μαθητές. Αλλά ακόμη και αν δεν είναι ήταν γνωστός, αυτό βγαίνει και με αναλυτική γεωμετρία αρκεί να γίνουν περισσότερες πράξεις.]
Θα βρω τις τιμές των

οι οποίες μεγιστοποιούν την ποσότητα

Θέτω λοιπόν

και παρατηρώ ότι

. Οπότε αρκεί να μεγιστοποιήσω το

και έτσι αποφεύγω την απόλυτη τιμή.
Είναι τώρα

όπου

και

.
Αν

, τότε

με ισότητα αν και μόνο αν

. Με λογισμό έχουμε μεγιστοποίηση όταν

. Από αυτά καταλήγουμε στα

και

.
Αν

τότε

με ισότητα αν και μόνο αν

. Με λογισμό έχουμε μεγιστοποίηση όταν

. Από αυτά καταλήγουμε στα

και

.
Οπότε και στις δύο περιπτώσεις βρίσκουμε τις συντεταγμένες

και

. (Η και το αντίστροφο αφού ελέγξαμε μόνο το

αντί το

|.)
[Στην προτεινόμενη λύση όπου έπαιρνε τα
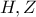
συμμετρικά, προχωρούσε πάλι με λογισμό για να βρει το μέγιστο της

. Το μέγιστο της

βρίσκεται με παρόμοιο τρόπο. Παρέλειψα τις πράξεις μιας και οι μέθοδοι από δω και πέρα είναι γνωστές.]
 με
με  . Δίνεται ισοσκελές τρίγωνο
. Δίνεται ισοσκελές τρίγωνο  εγγεγραμμένο στην έλλειψη με
εγγεγραμμένο στην έλλειψη με  και
και  . Δίνεται επίσης σημείο του επιπέδου
. Δίνεται επίσης σημείο του επιπέδου 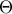 ώστε το
ώστε το  να είναι παραλληλόγραμμο.
να είναι παραλληλόγραμμο.  για τις οποίες το εμβαδόν του παραλληλογράμμου γίνεται μέγιστο.
για τις οποίες το εμβαδόν του παραλληλογράμμου γίνεται μέγιστο.
 . [Εν τέλει, η συνθήκη
. [Εν τέλει, η συνθήκη  δεν είναι ικανή από μόνη της για να μας δώσει ότι τα
δεν είναι ικανή από μόνη της για να μας δώσει ότι τα 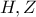 είναι συμμετρικά.]
είναι συμμετρικά.] που είναι παράλληλη στο μεγάλο
που είναι παράλληλη στο μεγάλο 

 τυχόν τρίγωνο του οποίου θεωρούμε την βάση
τυχόν τρίγωνο του οποίου θεωρούμε την βάση  ταυτιστεί με το
ταυτιστεί με το  . Αυτό είναι αρχικά αντιληπτό καθότι η διάμετρος
. Αυτό είναι αρχικά αντιληπτό καθότι η διάμετρος  είναι ο γ. τόπος των μέσων των χορδών που είναι παράλληλες στην
είναι ο γ. τόπος των μέσων των χορδών που είναι παράλληλες στην  ) . Συνεπώς για το μέγιστο τρίγωνο που είναι το
) . Συνεπώς για το μέγιστο τρίγωνο που είναι το  να είναι σημείο της διαμέσου
να είναι σημείο της διαμέσου  . Αν δράσουμε κυκλικά τότε παίρνουμε ότι το
. Αν δράσουμε κυκλικά τότε παίρνουμε ότι το  και
και  της έλλειψης.
της έλλειψης.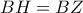 και θα βρω τις συνθήκες για τα
και θα βρω τις συνθήκες για τα  να είναι το μέγιστο δυνατό. Αν για αυτές τις τιμές ισχύει επιπλέον ότι
να είναι το μέγιστο δυνατό. Αν για αυτές τις τιμές ισχύει επιπλέον ότι  τότε τελείωσα. Το εμβαδόν του τριγώνου ισούται με
τότε τελείωσα. Το εμβαδόν του τριγώνου ισούται με 
 στο επίπεδο, το εμβαδόν του τριγώνου
στο επίπεδο, το εμβαδόν του τριγώνου  ισούται με το μισό της απόλυτης τιμής της ορίζουσας του πίνακα
ισούται με το μισό της απόλυτης τιμής της ορίζουσας του πίνακα
 οι οποίες μεγιστοποιούν την ποσότητα
οι οποίες μεγιστοποιούν την ποσότητα
 και παρατηρώ ότι
και παρατηρώ ότι  . Οπότε αρκεί να μεγιστοποιήσω το
. Οπότε αρκεί να μεγιστοποιήσω το  και έτσι αποφεύγω την απόλυτη τιμή.
και έτσι αποφεύγω την απόλυτη τιμή. 
 και
και  .
. , τότε
, τότε  με ισότητα αν και μόνο αν
με ισότητα αν και μόνο αν  . Με λογισμό έχουμε μεγιστοποίηση όταν
. Με λογισμό έχουμε μεγιστοποίηση όταν  . Από αυτά καταλήγουμε στα
. Από αυτά καταλήγουμε στα  και
και  .
. τότε
τότε  με ισότητα αν και μόνο αν
με ισότητα αν και μόνο αν  . Με λογισμό έχουμε μεγιστοποίηση όταν
. Με λογισμό έχουμε μεγιστοποίηση όταν  . Από αυτά καταλήγουμε στα
. Από αυτά καταλήγουμε στα  και
και  και
και  . (Η και το αντίστροφο αφού ελέγξαμε μόνο το
. (Η και το αντίστροφο αφού ελέγξαμε μόνο το  |.)
|.) . Το μέγιστο της
. Το μέγιστο της  (αυθαίρετα) οριζόντια "ανταμείφθηκαν πλουσιοπάροχα". Τα συμπεράσματα τα αφήνω στον κάθε ένα από μας.
(αυθαίρετα) οριζόντια "ανταμείφθηκαν πλουσιοπάροχα". Τα συμπεράσματα τα αφήνω στον κάθε ένα από μας.