Όμορφο γινόμενο με συνάρτηση Gamma

pprime · #1

Να αποδειχθεί ότι
$\displaystyle{\prod\limits_{k=1}^{+\infty }{\left( 1-\frac{z^{n}}{k^{n}} \right)}=\prod\limits_{k=0}^{n-1}{\frac{1}{\Gamma \left( 1-\exp \left( \frac{2\pi ik}{n} \right)z \right)}}}$

Tolaso J Kos · #2

pprime έγραψε:Για να αποδειχθεί ότι
$\displaystyle{\prod\limits_{k=1}^{+\infty }{\left( 1-\frac{z^{n}}{k^{n}} \right)}=\prod\limits_{k=0}^{n-1}{\frac{1}{\Gamma \left( 1-\exp \left( \frac{2\pi ik}{n} \right)z \right)}}}$

Αυτό είναι γνωστό αποτέλεσμα... μία απόδειξη που κυκλοφορεί εκεί έξω είναι η εξής:

Ξεκινάμε από τον ορισμό του ορίου της συνάρτησης $\Gamma$ του Euler που δεν είναι κανένας άλλος παρά ο επόμενος:
$\displaystyle{\Gamma(z) = \lim_{m \to +\infty} \frac{m! \ m^{z}}{z(z+1) \cdots (z+m)}}$ Τότε
$\displaystyle{\begin{aligned} \Gamma\left ( 1+z \right ) &= z \Gamma(z) \\ &= \lim_{m \to +\infty} \frac{m! \ m^{z}}{(z+1) \cdots (z+m)}\\ &= \lim_{m \to +\infty} m^{z} \prod_{k=1}^{m} \Big(1+ \frac{z}{k} \Big)^{-1} \end{aligned}}$ καθώς και
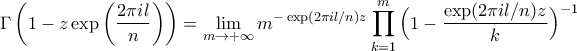$\displaystyle{\Gamma \left ( 1- z\exp \left ( \frac{2 \pi i l}{n} \right ) \right ) = \lim_{m \to +\infty} m^{-\exp(2 \pi i l /n)z} \prod_{k=1}^{m} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1}}$ Οπότε
$\displaystyle{\begin{aligned} \prod_{l=0}^{n-1} \Gamma \big[1-\exp(2 \pi i l/n)z \big] &= \lim_{m \to +\infty} m^{- \sum_{l=0}^{n-1} \exp(2 \pi i l/n)z} \prod_{l=0}^{n-1} \prod_{k=1}^{m} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1} \\ &= \lim_{m \to +\infty} \prod_{k=1}^{m} \prod_{l=0}^{n-1} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1} \end{aligned}}$ Όμως
$\displaystyle{x^n-z = \prod_{k=0}^{n-1} \left ( x - z^{1/n} \exp \left ( 2 \pi i k/n \right ) \right ) \Rightarrow 1-z = \prod_{k=0}^{n-1} \left ( 1 - z^{1/n} \exp \left ( 2 \pi i k/n \right ) \right)}$ και κατά συνέπεια
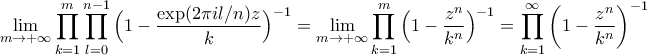$\displaystyle{\lim_{m \to +\infty} \prod_{k=1}^{m} \prod_{l=0}^{n-1} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1} = \lim_{m \to +\infty} \prod_{k=1}^{m} \Big( 1- \frac{z^{n}}{k^{n}} \Big) ^{-1} = \prod_{k=1}^{\infty} \left(1 - \frac{z^{n}}{k^{n}} \right)^{-1}}$ Υ.Σ: Από το παραπάνω τύπο προκύπτει τo εξής ( γνωστό ) αποτελέσμα:
$\displaystyle{\prod_{k=1}^{\infty} \left(1- \frac{z^{2}}{k^{2}} \right) = \frac{\sin \pi z}{\pi z}}$ Άσκηση: Κάντε χρήση του παραπάνω τύπου για να υπολογίσετε το γινόμενο:
$\displaystyle{\Pi = \prod_{k=2}^{\infty} \left(1- \frac{1}{k^{3}} \right)}$

pprime · #3

Tolaso J Kos έγραψε:
pprime έγραψε:Για να αποδειχθεί ότι
$\displaystyle{\prod\limits_{k=1}^{+\infty }{\left( 1-\frac{z^{n}}{k^{n}} \right)}=\prod\limits_{k=0}^{n-1}{\frac{1}{\Gamma \left( 1-\exp \left( \frac{2\pi ik}{n} \right)z \right)}}}$
Αυτό είναι γνωστό αποτέλεσμα... μία απόδειξη που κυκλοφορεί εκεί έξω είναι η εξής:

Ξεκινάμε από τον ορισμό του ορίου της συνάρτησης $\Gamma$ του Euler που δεν είναι κανένας άλλος παρά ο επόμενος:
$\displaystyle{\Gamma(z) = \lim_{m \to +\infty} \frac{m! \ m^{z}}{z(z+1) \cdots (z+m)}}$ Τότε
$\displaystyle{\begin{aligned} \Gamma\left ( 1+z \right ) &= z \Gamma(z) \\ &= \lim_{m \to +\infty} \frac{m! \ m^{z}}{(z+1) \cdots (z+m)}\\ &= \lim_{m \to +\infty} m^{z} \prod_{k=1}^{m} \Big(1+ \frac{z}{k} \Big)^{-1} \end{aligned}}$ καθώς και
$\displaystyle{\Gamma \left ( 1- z\exp \left ( \frac{2 \pi i l}{n} \right ) \right ) = \lim_{m \to +\infty} m^{-\exp(2 \pi i l /n)z} \prod_{k=1}^{m} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1}}$ Οπότε
$\displaystyle{\begin{aligned} \prod_{l=0}^{n-1} \Gamma \big[1-\exp(2 \pi i l/n)z \big] &= \lim_{m \to +\infty} m^{- \sum_{l=0}^{n-1} \exp(2 \pi i l/n)z} \prod_{l=0}^{n-1} \prod_{k=1}^{m} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1} \\ &= \lim_{m \to +\infty} \prod_{k=1}^{m} \prod_{l=0}^{n-1} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1} \end{aligned}}$ Όμως
$\displaystyle{x^n-z = \prod_{k=0}^{n-1} \left ( x - z^{1/n} \exp \left ( 2 \pi i k/n \right ) \right ) \Rightarrow 1-z = \prod_{k=0}^{n-1} \left ( 1 - z^{1/n} \exp \left ( 2 \pi i k/n \right ) \right)}$ και κατά συνέπεια
$\displaystyle{\lim_{m \to +\infty} \prod_{k=1}^{m} \prod_{l=0}^{n-1} \Big(1- \frac{\exp(2 \pi i l/n)z}{k} \Big)^{-1} = \lim_{m \to +\infty} \prod_{k=1}^{m} \Big( 1- \frac{z^{n}}{k^{n}} \Big) ^{-1} = \prod_{k=1}^{\infty} \left(1 - \frac{z^{n}}{k^{n}} \right)^{-1}}$ Υ.Σ: Από το παραπάνω τύπο προκύπτει τo εξής ( γνωστό ) αποτελέσμα:
$\displaystyle{\prod_{k=1}^{\infty} \left(1- \frac{z^{2}}{k^{2}} \right) = \frac{\sin \pi z}{\pi z}}$ Άσκηση: Κάντε χρήση του παραπάνω τύπου για να υπολογίσετε το γινόμενο:
$\displaystyle{\Pi = \prod_{k=2}^{\infty} \left(1- \frac{1}{k^{3}} \right)}$

pprime · #4

https://de.wikibooks.org/wiki/Formelsam ... rodukte#20

Όμορφο γινόμενο με συνάρτηση Gamma

Όμορφο γινόμενο με συνάρτηση Gamma

Re: Όμορφο γινόμενο με συνάρτηση Gamma

Re: Όμορφο γινόμενο με συνάρτηση Gamma

Re: Όμορφο γινόμενο με συνάρτηση Gamma

Μέλη σε σύνδεση