m.pαpαgrigorakis έγραψε:
Μάκη δεν έχω μελετήσει αναλυτικά τις οδηγίες επειδή δεν διδάσκω φέτος στην Α Λυκείου. Αυτός είναι ο λόγος που έβαλα και το σχόλιο ότι "πιθανόν κάποια ερωτήματα να ξεφεύγουν από το αυστηρό πλαίσιο της διδακτέας ύλης"
Τις ασκήσεις αυτές τις συνθέτω τις τελευταίες μέρες. Τις δίνω για επανάληψη στο γιος μου που πάει στην Α Λυκείου.
Σκέφτηκα ότι ίσως φανούν χρήσιμες και σε κάποιον άλλο, αφού βέβαια τις προσαρμόσει κατάλληλα για αυτό και τις ανεβάζω εδώ.
Αρχικά
Μίλτο πρέπει να ομολογήσω ότι κάνεις μια αξιέπαινη προσπάθεια στην Α΄ Λυκείου, όπως αξιοσημείωτο είναι και το ενδιαφέρον που δείχνει ο Στάθης με τις όμορφες λύσεις που μας παρουσιάζει.
Νομίζω ότι έχετε υποχρέωση να τα μαζέψετε και να τα κάνετε ένα όμορφο φυλλαδιάκι!!
Ένσταση! Μιας που κάνεις τον κόπο (ή κάνετε), γιατί δεν θέτεις ασκήσεις εντός της ύλης, να φανούν χρήσιμες σε όλους αλλά και στον υιό σου;;
Όλοι μας έχουμε σημειώσεις - ασκήσεις από την παλιά ύλη - βιβλίο, άρα θα ήταν ωφέλιμο να φρεσκάρουμε τα αρχεία μας με νέα σύγχρονα θέματα προσαρμοσμένα στο νέο βιβλίο, στην νέα ύλη και να μην αναπαράγουμε παλιές ασκήσεις, τι λες;;
Δίνω μια άσκηση με αυτό το σκεπτικό!!
Άσκηση 6η
Δίνεται το τριώνυμο

, όπου λ πραγματικός αριθμός.
α. Να αποδείξετε ότι η διακρίνουσα του τριωνύμου ισούται με: Δ = 4(λ – 5)(λ – 3).
β. Να βρείτε για ποιες τιμές του πραγματικού αριθμού λ το τριώνυμο έχει δύο ρίζες πραγματικές και άνισες.
γ. Αν

,

είναι οι άνισες ρίζες του τριωνύμου, να βρείτε το λ αν ισχύει:

= 0,75
δ. Να βρείτε τις τιμές του

ώστε

για κάθε πραγματικό αριθμό x.
Σημείωση: Αν θέλουμε να το ψειρίσουμε και το γ υποερώτημα είναι εκτός του πνεύματος του νέου βιβλίου...
edit: διόρθωση του Latex με
με  .
. έχει δύο ρίζες πραγματικές και άνισες για κάθε
έχει δύο ρίζες πραγματικές και άνισες για κάθε  .
. ώστε η συνάρτηση
ώστε η συνάρτηση 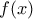 με
με  να έχει ελάχιστο στο
να έχει ελάχιστο στο  .
. 

 τέμνει τους άξονες
τέμνει τους άξονες  και
και 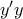

 είναι πάνω από την ευθεία
είναι πάνω από την ευθεία 
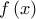 και το σημείο στο οποίο η
και το σημείο στο οποίο η 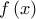 τέμνει τον
τέμνει τον 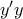

 για κάθε
για κάθε  οπότε η εξίσωση έχει δύο ρίζες πραγματικές και άνισες
οπότε η εξίσωση έχει δύο ρίζες πραγματικές και άνισες
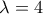 έχουμε:
έχουμε:  οπότε από την ανίσωση έχουμε:
οπότε από την ανίσωση έχουμε:

![\displaystyle{
\boxed{x \in \left( { - \infty , - 3} \right] \cup \left[ { - 1,0} \right)}
} \displaystyle{
\boxed{x \in \left( { - \infty , - 3} \right] \cup \left[ { - 1,0} \right)}
}](/forum/ext/geomar/texintegr/latexrender/pictures/f2483bc083cbbabf514e79f73df99e2d.png)




![\displaystyle{
\left\{ \begin{gathered}
\left\{ \begin{gathered}
x^2 - 4x + 3 = x - 1 \hfill \\
x \in \left( { - \infty ,1} \right] \cup \left[ {3, + \infty } \right) \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
- x^2 + 4x - 3 = x - 1 \hfill \\
x \in \left( {1,3} \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \ldots \left\{ \begin{gathered}
\left\{ \begin{gathered}
x^2 - 5x + 4 = 0 \hfill \\
x \in \left( { - \infty ,1} \right] \cup \left[ {3, + \infty } \right) \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x^2 - 3x + 2 = 0 \hfill \\
x \in \left( {1,3} \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left\{ \begin{gathered}
\boxed{x = 1,x = 4} \hfill \\
x \in \left( { - \infty ,1} \right] \cup \left[ {3, + \infty } \right) \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x = 1(\alpha \pi o\rho ),\boxed{x = 2} \hfill \\
x \in \left( {1,3} \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.
} \displaystyle{
\left\{ \begin{gathered}
\left\{ \begin{gathered}
x^2 - 4x + 3 = x - 1 \hfill \\
x \in \left( { - \infty ,1} \right] \cup \left[ {3, + \infty } \right) \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
- x^2 + 4x - 3 = x - 1 \hfill \\
x \in \left( {1,3} \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \ldots \left\{ \begin{gathered}
\left\{ \begin{gathered}
x^2 - 5x + 4 = 0 \hfill \\
x \in \left( { - \infty ,1} \right] \cup \left[ {3, + \infty } \right) \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x^2 - 3x + 2 = 0 \hfill \\
x \in \left( {1,3} \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left\{ \begin{gathered}
\boxed{x = 1,x = 4} \hfill \\
x \in \left( { - \infty ,1} \right] \cup \left[ {3, + \infty } \right) \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x = 1(\alpha \pi o\rho ),\boxed{x = 2} \hfill \\
x \in \left( {1,3} \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.
}](/forum/ext/geomar/texintegr/latexrender/pictures/4bd21cca26bbdc870e3d129f11991d55.png)




 και με
και με 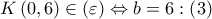
 και
και 


 είναι περιττή
είναι περιττή τέμνει τις ευθείες
τέμνει τις ευθείες  ,
, 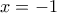 ,
,  ή
ή 
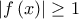
 ,
,  , και
, και  είναι συνευθειακά.
είναι συνευθειακά.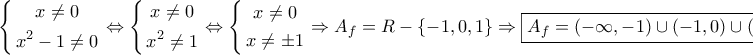

 παριστάνει το πεδίο ορισμού της f
παριστάνει το πεδίο ορισμού της f και
και  άρα η f είναι περιττή
άρα η f είναι περιττή με
με  γνησίως φθίνουσα στο
γνησίως φθίνουσα στο  .
.  με
με  γνησίως φθίνουσα στο
γνησίως φθίνουσα στο 
 τελικά η f είναι γνησίως φθίνουσα στο
τελικά η f είναι γνησίως φθίνουσα στο 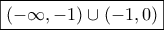
 με
με  γνησίως φθίνουσα στο
γνησίως φθίνουσα στο  .
. με
με  γνησίως φθίνουσα στο
γνησίως φθίνουσα στο 
 τελικά η f είναι γνησίως φθίνουσα στο
τελικά η f είναι γνησίως φθίνουσα στο 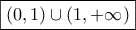

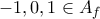 προφανώς η
προφανώς η  δεν τέμνει τις (κατακόρυφες) ευθείες με εξισώσεις
δεν τέμνει τις (κατακόρυφες) ευθείες με εξισώσεις  αλλά και επειδή
αλλά και επειδή 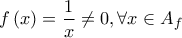 η
η 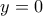 (τον άξονα x'x)
(τον άξονα x'x)
 ,
,  και
και 
 και από το σημείο
και από το σημείο  .
.

 οι συντεταγμένες και του Α επαληθεύουν την εξίσωση της
οι συντεταγμένες και του Α επαληθεύουν την εξίσωση της 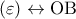 οπότε το σημεία Ο, Α, Β είναι συνευθειακά.
οπότε το σημεία Ο, Α, Β είναι συνευθειακά. ,
,  είναι συμμετρικά ως προς το
είναι συμμετρικά ως προς το 
 είναι συνευθειακά.
είναι συνευθειακά. με .
με .

 και
και 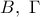 είναι τα κοινά σημεία της γραφικής παράστασης της συνάρτησης
είναι τα κοινά σημεία της γραφικής παράστασης της συνάρτησης  είναι
είναι 
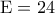
 , να κάνετε πίνακα μονοτονίας και ακροτάτων της
, να κάνετε πίνακα μονοτονίας και ακροτάτων της 
![\displaystyle{
\Delta = \left[ { - 2\left( {\lambda + 2} \right)} \right]^2 - 32\lambda = 4\left( {\lambda + 2} \right)^2 - 32\lambda = 4\left[ {\left( {\lambda + 2} \right)^2 - 8\lambda } \right] \Rightarrow \ldots \boxed{\Delta = 4\left( {\lambda - 2} \right)^2 \geqslant 0,\forall \lambda \in R}
} \displaystyle{
\Delta = \left[ { - 2\left( {\lambda + 2} \right)} \right]^2 - 32\lambda = 4\left( {\lambda + 2} \right)^2 - 32\lambda = 4\left[ {\left( {\lambda + 2} \right)^2 - 8\lambda } \right] \Rightarrow \ldots \boxed{\Delta = 4\left( {\lambda - 2} \right)^2 \geqslant 0,\forall \lambda \in R}
}](/forum/ext/geomar/texintegr/latexrender/pictures/ab2ffc174fbfa9c389cb53f6d3b8f7de.png)
 θα έχει ρίζες τις
θα έχει ρίζες τις 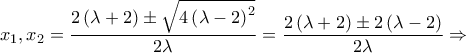





 με
με  οπότε με
οπότε με  έχουμε:
έχουμε:![\displaystyle{
\left( { - \infty ,\frac{3}
{2}} \right]
} \displaystyle{
\left( { - \infty ,\frac{3}
{2}} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/5be79236952dac91f7fe31103aaa3034.png) και
και 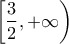
 το
το 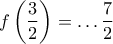
 με
με 
 τότε:
τότε:![\sqrt {3\sqrt[3]{{f\left( {18} \right)}}} \sqrt {3\sqrt[3]{{f\left( {18} \right)}}}](/forum/ext/geomar/texintegr/latexrender/pictures/bc6d1c3a61f08db9cfb20fb7c286501a.png)
 και
και 


 έχουμε:
έχουμε: 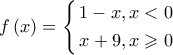
![\displaystyle{
f\left( {18} \right) = 18 + 9 = 27 \Rightarrow \sqrt[3]{{f\left( {18} \right)}} = \sqrt[3]{{27}} = 3 \Rightarrow \sqrt {3 \cdot \sqrt[3]{{f\left( {18} \right)}}} = \sqrt 9 = 3
} \displaystyle{
f\left( {18} \right) = 18 + 9 = 27 \Rightarrow \sqrt[3]{{f\left( {18} \right)}} = \sqrt[3]{{27}} = 3 \Rightarrow \sqrt {3 \cdot \sqrt[3]{{f\left( {18} \right)}}} = \sqrt 9 = 3
}](/forum/ext/geomar/texintegr/latexrender/pictures/11fe2e6cacb9534a279ada17cfc135c7.png)
 και
και 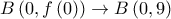 θα είναι
θα είναι 
 και
και  δηλαδή η γραφική παράσταση της f δεν τέμνει τον άξονα x’x
δηλαδή η γραφική παράσταση της f δεν τέμνει τον άξονα x’x![\displaystyle{
f\left( x \right) \leqslant 9 \Leftrightarrow \left\{ \begin{gathered}
\left\{ \begin{gathered}
1 - x \leqslant 9 \hfill \\
x < 0 \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x + 9 \leqslant 9 \hfill \\
x \geqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left\{ \begin{gathered}
x \geqslant - 8 \hfill \\
x < 0 \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x \leqslant 0 \hfill \\
x \geqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x \in \left[ { - 8,0} \right) \hfill \\
v \hfill \\
x = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \boxed{x \in \left[ { - 8,0} \right]}
} \displaystyle{
f\left( x \right) \leqslant 9 \Leftrightarrow \left\{ \begin{gathered}
\left\{ \begin{gathered}
1 - x \leqslant 9 \hfill \\
x < 0 \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x + 9 \leqslant 9 \hfill \\
x \geqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left\{ \begin{gathered}
x \geqslant - 8 \hfill \\
x < 0 \hfill \\
\end{gathered} \right. \hfill \\
v \hfill \\
\left\{ \begin{gathered}
x \leqslant 0 \hfill \\
x \geqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x \in \left[ { - 8,0} \right) \hfill \\
v \hfill \\
x = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \boxed{x \in \left[ { - 8,0} \right]}
}](/forum/ext/geomar/texintegr/latexrender/pictures/0b086a8c962402efb8e78b7f4e75eb81.png)
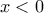 επειδή ο τύπος της f είναι τύπος ευθείες με συντελεστή διεύθυνσης -1 η f θα είναι γνησίως φθίνουσα στο
επειδή ο τύπος της f είναι τύπος ευθείες με συντελεστή διεύθυνσης -1 η f θα είναι γνησίως φθίνουσα στο 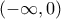
 επειδή ο τύπος της f είναι τύπος ευθείες με συντελεστή διεύθυνσης 1 η f θα είναι γνησίως αύξουσα στο
επειδή ο τύπος της f είναι τύπος ευθείες με συντελεστή διεύθυνσης 1 η f θα είναι γνησίως αύξουσα στο 
 με
με  και
και  . Γνωρίζουμε ότι για
. Γνωρίζουμε ότι για  .
. και
και  και
και 
 με
με 



 \displaystyle{\displaystyle{
\displaystyle{\displaystyle{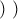 \displaystyle{
\displaystyle{ \displaystyle{
\displaystyle{

![\displaystyle{
- x^2 + 4x + 5 \geqslant 0\mathop \Leftrightarrow \limits^{ - x^2 + 4x + 5 = 0 \Leftrightarrow x = - 1,x = 5} \boxed{x \in \left[ { - 1,5} \right]}
} \displaystyle{
- x^2 + 4x + 5 \geqslant 0\mathop \Leftrightarrow \limits^{ - x^2 + 4x + 5 = 0 \Leftrightarrow x = - 1,x = 5} \boxed{x \in \left[ { - 1,5} \right]}
}](/forum/ext/geomar/texintegr/latexrender/pictures/4661db1570e43e3c33ab5b4d2a082254.png)
![\displaystyle{
\left( { - \infty , - \frac{\beta }
{{2\alpha }}} \right] \to \boxed{\left( { - \infty ,1} \right]}
} \displaystyle{
\left( { - \infty , - \frac{\beta }
{{2\alpha }}} \right] \to \boxed{\left( { - \infty ,1} \right]}
}](/forum/ext/geomar/texintegr/latexrender/pictures/d153b5904b70587c38bbdab80dafa84e.png) και γνησίως αύξουσα στο διάστημα
και γνησίως αύξουσα στο διάστημα 
 \displaystyle{\displaystyle{
\displaystyle{\displaystyle{ \displaystyle{
\displaystyle{ \displaystyle{
\displaystyle{


 παρουσιάζει ακρότατο στη θέση
παρουσιάζει ακρότατο στη θέση  το
το  . Άρα
. Άρα 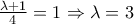 και
και  .
. . Επομένως
. Επομένως  το οποίο ισχύει για
το οποίο ισχύει για  .
. . Πρέπει
. Πρέπει 
![\Rightarrow x\epsilon \left[-1,5 \right] \Rightarrow x\epsilon \left[-1,5 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b0e3c442698de26f1c1c2518bd0d0774.png) .
.![(-\propto ,1] (-\propto ,1]](/forum/ext/geomar/texintegr/latexrender/pictures/255c5144ca6fcdfdded8c2eaffe6875b.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 


 . Άρα η γραφική παράσταση της συνάρτησης g τέμνει τον άξονα των y στο σημείο
. Άρα η γραφική παράσταση της συνάρτησης g τέμνει τον άξονα των y στο σημείο 
 x=-1 ή x=5. Άρα η γραφική παράσταση της συνάρτησης g τέμνει τον άξονα των x στα σημεία
x=-1 ή x=5. Άρα η γραφική παράσταση της συνάρτησης g τέμνει τον άξονα των x στα σημεία 
 προκύπτουν
προκύπτουν 
 , όπου λ πραγματικός αριθμός.
, όπου λ πραγματικός αριθμός. ,
,  είναι οι άνισες ρίζες του τριωνύμου, να βρείτε το λ αν ισχύει:
είναι οι άνισες ρίζες του τριωνύμου, να βρείτε το λ αν ισχύει: = 0,75
= 0,75 ώστε
ώστε  για κάθε πραγματικό αριθμό x.
για κάθε πραγματικό αριθμό x.