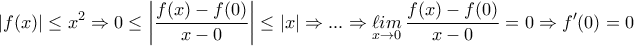Ας φτιάξουμε στο φάκελλο αυτό μια σειρά ασκήσεων σε όλη την ύλη, από απλές έως θέματα εξετάσεων.
Ξεκινάω με τη πρώτη τριάδα θεμάτων: Μιγαδικοί, Όρια , Παράγωγοι
Άσκηση 1
Δίνονται οι μιγαδικοί
 και
και  ,
,  . Αν
. Αν  , να δειχθεί ότι:
, να δειχθεί ότι: 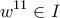 .
.Άσκηση 2*
Έστω η συνάρτηση
 με την ιδιότητα
με την ιδιότητα ![\displaystyle{2\left[ {f\left( {\frac{x}{y}} \right) + f\left( {\frac{x}{w}} \right)} \right] - f(x)f\left( {\frac{{y + w}}{2}} \right) \ge 4} \displaystyle{2\left[ {f\left( {\frac{x}{y}} \right) + f\left( {\frac{x}{w}} \right)} \right] - f(x)f\left( {\frac{{y + w}}{2}} \right) \ge 4}](/forum/ext/geomar/texintegr/latexrender/pictures/e166a5942b95c92cd4704418adb40a86.png) για κάθε
για κάθε  .
.Να υπολογισθούν τα όρια:
i.

ii.
 .
.iii.
 .
.Άσκηση 3*
Έστω η παραγωγίσιμη συνάρτηση
 με f(0)=0 και για την οποία ισχύει για κάθε
με f(0)=0 και για την οποία ισχύει για κάθε  ότι:
ότι: . Να δειχθεί ότι υπάρχει
. Να δειχθεί ότι υπάρχει  ώστε να ισχύει:
ώστε να ισχύει:  για κάθε
για κάθε  .
.Να έχουμε μια καλή μέρα,
Θωμάς

 ,
, .
. , άρα
, άρα  ,
, 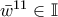 ή
ή 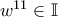 .
. .
.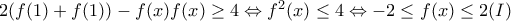 .
. .
. .
.
 ,
,
 .
. η αρχική σχέση γίνεται:
η αρχική σχέση γίνεται: .
. έχουμε:
έχουμε: ,
, (και αφού η f είναι παραγωγίσιμη) βρίσκουμε ότι:
(και αφού η f είναι παραγωγίσιμη) βρίσκουμε ότι: 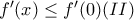
 έχουμε:
έχουμε: ,
, (και αφού η f είναι παραγωγίσιμη) βρίσκουμε ότι:
(και αφού η f είναι παραγωγίσιμη) βρίσκουμε ότι: 
 ,οπότε
,οπότε  , όπου c σταθερά.
, όπου c σταθερά. .
. . Να αποδειχθεί ότι η εξίσωση
. Να αποδειχθεί ότι η εξίσωση  έχει μια τουλάχιστον λύση στο
έχει μια τουλάχιστον λύση στο ![(0,\frac{\pi }{2}] (0,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/b89536b2363697c1fc0e5893c8b88eb3.png)

 , ρίζα της εξίσωσης είναι το
, ρίζα της εξίσωσης είναι το  .
. 
![\displaystyle{g:\Big[0,\frac{\pi}{2}\Big]\rightarrow \mathbb{R}} \displaystyle{g:\Big[0,\frac{\pi}{2}\Big]\rightarrow \mathbb{R}}](/forum/ext/geomar/texintegr/latexrender/pictures/ece27564dcdd6180f9fa9ea1568c0afd.png) με
με 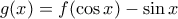
![\displaystyle{\Big[0,\frac{\pi}{2}\Big]} \displaystyle{\Big[0,\frac{\pi}{2}\Big]}](/forum/ext/geomar/texintegr/latexrender/pictures/5ab1da2786b0e04be55e087a173a29c7.png) και
και 

 ,
,  .
.  , άρα είναι γν. φθίνουσα στο
, άρα είναι γν. φθίνουσα στο  . Τέλος
. Τέλος  και
και  . Από μονοτονία + θ. Bolzano παίρνουμε το ζητούμενο.
. Από μονοτονία + θ. Bolzano παίρνουμε το ζητούμενο.
 Αν
Αν  να δειχθεί ότι η
να δειχθεί ότι η  δεν μπορεί να είναι συνεχής στο
δεν μπορεί να είναι συνεχής στο 
 είναι συνεχής στο
είναι συνεχής στο 
 και προκύπτει
και προκύπτει  άρα
άρα  δηλαδή
δηλαδή 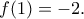
![\displaystyle{[0,1]} \displaystyle{[0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/1109a14ceae9f7dfdce6cfbb76246020.png) και λαμβάνει ετερόσημες τιμές στα άκρα του διαστήματος.
και λαμβάνει ετερόσημες τιμές στα άκρα του διαστήματος.  τέτοιο ώστε
τέτοιο ώστε 
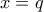 , προκύπτει
, προκύπτει  δηλαδή
δηλαδή 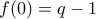 άρα
άρα  , άτοπο.
, άτοπο.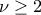 .
. για κάθε
για κάθε  ισχύει:
ισχύει: 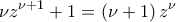 , να δειχθεί ότι
, να δειχθεί ότι  .
. και ν περιττός με
και ν περιττός με  .
. με
με  .
.
 ,
, ,
,![(-\infty,1] (-\infty,1]](/forum/ext/geomar/texintegr/latexrender/pictures/6a1672dd28da95aacd838a7cd55045ed.png)
 .
.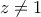 , έχουμε ότι:
, έχουμε ότι:





 ,
,  .
.
 ο οποίος να βρεθεί.
ο οποίος να βρεθεί. έχουμε
έχουμε 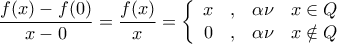

 Έστω η γνησίως αύξουσα συνάρτηση
Έστω η γνησίως αύξουσα συνάρτηση  , για την οποία ισχύει
, για την οποία ισχύει  , για κάθε
, για κάθε  .
. τέτοιο ώστε
τέτοιο ώστε 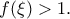
 , για κάθε
, για κάθε 
 για κάθε
για κάθε  και να χρησιμοποιήσουμε το κριτήριο παρεμβολής.
και να χρησιμοποιήσουμε το κριτήριο παρεμβολής.
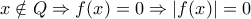 , επομένως
, επομένως