 συνεχής και μη σταθερή. Υποθέτουμε ότι υπάρχει συνάρτηση
συνεχής και μη σταθερή. Υποθέτουμε ότι υπάρχει συνάρτηση  ώστε
ώστε  για κάθε
για κάθε  . Αποδείξτε ότι η
. Αποδείξτε ότι η  είναι γνησίως μονότονη.
είναι γνησίως μονότονη.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 συνεχής και μη σταθερή. Υποθέτουμε ότι υπάρχει συνάρτηση
συνεχής και μη σταθερή. Υποθέτουμε ότι υπάρχει συνάρτηση  ώστε
ώστε  για κάθε
για κάθε  . Αποδείξτε ότι η
. Αποδείξτε ότι η  είναι γνησίως μονότονη.
είναι γνησίως μονότονη.Αρκεί να αποδείξουμε ότι ηpeter έγραψε:Έστωσυνεχής και μη σταθερή. Υποθέτουμε ότι υπάρχει συνάρτηση
ώστε
για κάθε
. Αποδείξτε ότι η
είναι γνησίως μονότονη.
 είναι 1-1. Έστω ότι αληθεύει το αντίθετο.
είναι 1-1. Έστω ότι αληθεύει το αντίθετο. 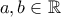 (χωρίς βλάβη
(χωρίς βλάβη  ) ώστε
) ώστε  .
. είναι συνεχής, μη σταθερή και
είναι συνεχής, μη σταθερή και  , τότε το γράφημα της
, τότε το γράφημα της![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) οσοδήποτε μικρές θέλουμε οριζόντιες χορδές, δηλαδή για κάθε
οσοδήποτε μικρές θέλουμε οριζόντιες χορδές, δηλαδή για κάθε 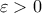 υπάρχουν
υπάρχουν ![x_1,x_2 \in [a,b] x_1,x_2 \in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/59f3dc726effaec2393e0be638448484.png) με
με  , άρα
, άρα  , άρα η
, άρα η  είναι περιοδική, χωρίς ελάχιστη θετική περίοδο.
είναι περιοδική, χωρίς ελάχιστη θετική περίοδο.Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 2 επισκέπτες