Ας δούμε μία απόδειξη του Λήμματος, που δεν έχει τύχει να τη δω στην βιβλιογραφία που έχω υπόψη μου. Προέκυψε από την ανάγνωση της λύσης του Ανδρέα πιο πάνω ( ανάρτηση #16 ) ως μία αναλυτική μεταγραφή του κειμένου.

Έστω

το ισοσκελές τρίγωνο προς το μέρος της

που δεν κείται το

, με

και

.
Τα τρίγωνα
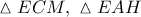
είναι όμοια γιατί έχουν

και
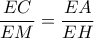
και άρα, ισχύει
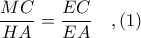
Ομοίως, από τα όμοια τρίγωνα

, γιατί έχουν

και
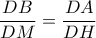
, έχουμε
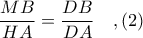
Από
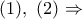
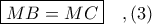
λόγω
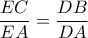

- Όμοια ισοσκελή τρίγωνα - Απόδειξη του Λήμματος στο #11
- f=181 t=72025 (3b).PNG (19.61 KiB) Προβλήθηκε 1805 φορές

Έστω τα σημεία

και

.
Από


λόγω της ομοιότητας των τριγώνων
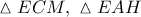

προκύπτει ότι το τετράπλευρο

είναι εγγράψιμο
και επομένως ισχύει

Από


λόγω της ομοιότητας των τριγώνων


έχουμε ότι το τετράπλευρο
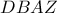
είναι εγγράψιμο
και άρα ισχύει
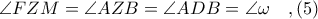
Από
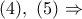
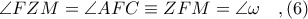
Από
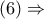
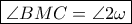
και το
Λήμμα έχει αποδειχθεί.
Κώστας Βήττας.
ΥΓ. Είναι προφανές ότι λόγω του ισοσκελούς τριγώνου

η ευθεία

, ως παράλληλη προς την διχοτόμο της γωνίας
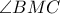
του ισοσκελούς τριγώνου

, είναι κάθετη επί την

όπως καταλήγει ο Ανδρέας στην λύση του ( #16 ).
 και εξωτερικά αυτού, κατασκευάζουμε τα όμοια ισοσκελή τρίγωνα
και εξωτερικά αυτού, κατασκευάζουμε τα όμοια ισοσκελή τρίγωνα  . Κατασκευάζουμε άλλο ένα όμοιο προς αυτά τρίγωνο
. Κατασκευάζουμε άλλο ένα όμοιο προς αυτά τρίγωνο  καθώς και το συμμετρικό του
καθώς και το συμμετρικό του  ως προς
ως προς  σημείο
σημείο  . Αν
. Αν  είναι τα ορθόκεντρα των
είναι τα ορθόκεντρα των 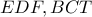 αντίστοιχα, να αποδείξετε ότι:
αντίστοιχα, να αποδείξετε ότι: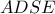 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. και
και 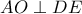 .
.
 , κατασκευάζουμε τα όμοια ισοσκελή τρίγωνα
, κατασκευάζουμε τα όμοια ισοσκελή τρίγωνα  προς το εξωτερικό μέρος του τριγώνου και το
προς το εξωτερικό μέρος του τριγώνου και το  προς το εσωτερικό μέρος αυτού. Αποδείξτε ότι το τετράπλευρο
προς το εσωτερικό μέρος αυτού. Αποδείξτε ότι το τετράπλευρο 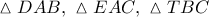 . Αποδείξτε ότι
. Αποδείξτε ότι  είναι το ορθόκεντρο του
είναι το ορθόκεντρο του 
 δοσμένου τριγώνου
δοσμένου τριγώνου  , το όμοιο με τα προηγούμενα ισοσκελές τρίγωνο, προς το μέρος της
, το όμοιο με τα προηγούμενα ισοσκελές τρίγωνο, προς το μέρος της  που δεν κείται το
που δεν κείται το  είναι το ορθόκεντρο του
είναι το ορθόκεντρο του 
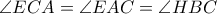 Άρα το
Άρα το 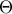 . Άρα
. Άρα 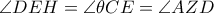
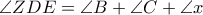
 (από το τρίγωνο ΔΗΓ)
(από το τρίγωνο ΔΗΓ) (αφού
(αφού  λόγω της ομοιότητας των ισοσκελών τριγώνων
λόγω της ομοιότητας των ισοσκελών τριγώνων 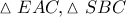 ) από την οποία ομοιότητα προκύπτει ότι:
) από την οποία ομοιότητα προκύπτει ότι:  . Με ακριβώς όμοιο τρόπο προκύπτει ότι:
. Με ακριβώς όμοιο τρόπο προκύπτει ότι:  . Από
. Από  και επειδή οι ομόλογες πλευρές τους
και επειδή οι ομόλογες πλευρές τους 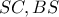 είναι ίσες (λόγω του ισοσκελούς
είναι ίσες (λόγω του ισοσκελούς  και
και 
 παραλληλόγραμμο (οι απέναντι πλευρές του είναι ίσες) και το ζητούμενο έχει αποδειχθεί.
παραλληλόγραμμο (οι απέναντι πλευρές του είναι ίσες) και το ζητούμενο έχει αποδειχθεί. οι κύκλοι κέντρων
οι κύκλοι κέντρων  αντίστοιχα και ακτινών
αντίστοιχα και ακτινών  αντίστοιχα και ας είναι
αντίστοιχα και ας είναι  ) κοινό σημείο τομής τους. Τότε
) κοινό σημείο τομής τους. Τότε  και συνεπως
και συνεπως  είναι διχοτόμος της
είναι διχοτόμος της  και
και  εγγράψιμο σε κύκλο και με
εγγράψιμο σε κύκλο και με  ισοσκελές λόγω των υψών και του ισοσκελούς τριγώνου
ισοσκελές λόγω των υψών και του ισοσκελούς τριγώνου  ) η διχοτόμος της
) η διχοτόμος της 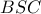 (δηλαδή η
(δηλαδή η  ) θα διέρχεται από το
) θα διέρχεται από το  συνευθειακά, δηλαδή
συνευθειακά, δηλαδή  και προφανώς
και προφανώς 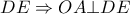 και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί . Έστω
Έστω  οι προβολές του σημείου
οι προβολές του σημείου  αντιστοίχως και έστω τα σημεία
αντιστοίχως και έστω τα σημεία  και
και  .
. έχουμε ότι τα ορθογώνια τρίγωνα
έχουμε ότι τα ορθογώνια τρίγωνα 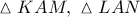 είναι όμοια
είναι όμοια
 τώρα, προκύπτει ότι τα σημεία
τώρα, προκύπτει ότι τα σημεία  είναι ομοκυκλικά και επομένως
είναι ομοκυκλικά και επομένως 

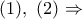

 , σύμφωνα με το
, σύμφωνα με το  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. του δοσμένου τριγώνου
του δοσμένου τριγώνου  , αντιστοίχως.
, αντιστοίχως. , λόγω
, λόγω  και
και 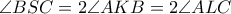 .
. των πλευρών του τριγώνου
των πλευρών του τριγώνου  , προκύπτει άμεσα ότι το τετράπλευρο
, προκύπτει άμεσα ότι το τετράπλευρο  με
με  και ισογώνιες τις υποτείνουσες ως προς τη γωνία
και ισογώνιες τις υποτείνουσες ως προς τη γωνία  . Αποδείξτε ότι το τρίγωνο
. Αποδείξτε ότι το τρίγωνο 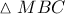 είναι ισοσκελές με
είναι ισοσκελές με  και
και  , όπου
, όπου  είναι το μέσον του τμήματος
είναι το μέσον του τμήματος 
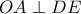 αρκεί να αποδειχθεί ότι
αρκεί να αποδειχθεί ότι 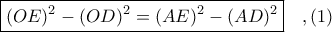
 τα μέσα των πλευρών
τα μέσα των πλευρών  και
και  .
. και
και 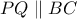 , έχουμε ότι και το τρίγωνο
, έχουμε ότι και το τρίγωνο  είναι ισοσκελές με
είναι ισοσκελές με 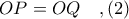
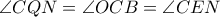 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο σε κύκλο με διάμετρο
είναι εγγράψιμο σε κύκλο με διάμετρο 
 και ομοίως έχουμε
και ομοίως έχουμε 
 , σύμφωνα με το
, σύμφωνα με το 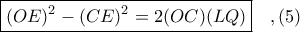
 είναι το μέσον του
είναι το μέσον του  .
. έχουμε
έχουμε  όπου
όπου  είναι το μέσον του
είναι το μέσον του  .
.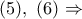
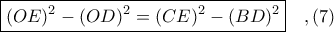 λόγω
λόγω  .
.
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. είναι όμοια μέσω μετασχηματισμού ομοιότητας λόγου
είναι όμοια μέσω μετασχηματισμού ομοιότητας λόγου  και γωνίας
και γωνίας  της βάσης των όμοιων ισοσκελών τριγώνων. Μέσω του παραπάνω μετασχηματισμού, η εικόνα του
της βάσης των όμοιων ισοσκελών τριγώνων. Μέσω του παραπάνω μετασχηματισμού, η εικόνα του  είναι το
είναι το 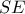 . Το
. Το  έχουν ίδια σχέση αναλογίας και γωνίας. Επομένως τα
έχουν ίδια σχέση αναλογίας και γωνίας. Επομένως τα  είναι παράλληλα και ίσα.
είναι παράλληλα και ίσα.
 τα μέσα των αντίστοιχων πλευρών.
τα μέσα των αντίστοιχων πλευρών. 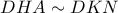 και
και  οι οποίες έχουν ίσους λόγους και γωνίες, προκύπτει ότι
οι οποίες έχουν ίσους λόγους και γωνίες, προκύπτει ότι  καθώς και ότι η
καθώς και ότι η  σχηματίζει ίσες γωνίες με τα σκέλη του ισοσκελούς τριγώνου
σχηματίζει ίσες γωνίες με τα σκέλη του ισοσκελούς τριγώνου  , επομένως είναι κάθετη στην βάση του
, επομένως είναι κάθετη στην βάση του  άρα και στην
άρα και στην  οι προβολές των
οι προβολές των  στις πλευρές
στις πλευρές  αντίστοιχα και
αντίστοιχα και 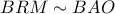 και
και 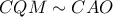 οι οποίες έχουν ίσους λόγους και γωνίες, προκύπτει ότι
οι οποίες έχουν ίσους λόγους και γωνίες, προκύπτει ότι 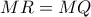 καθώς και ότι η
καθώς και ότι η  σχηματίζει ίσες γωνίες με τα σκέλη του ισοσκελούς τριγώνου
σχηματίζει ίσες γωνίες με τα σκέλη του ισοσκελούς τριγώνου 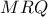 , επομένως είναι κάθετη στην βάση του
, επομένως είναι κάθετη στην βάση του 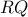 άρα και στην
άρα και στην  το ισοσκελές τρίγωνο προς το μέρος της
το ισοσκελές τρίγωνο προς το μέρος της  και
και  .
.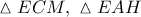 είναι όμοια γιατί έχουν
είναι όμοια γιατί έχουν  και
και 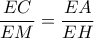 και άρα, ισχύει
και άρα, ισχύει 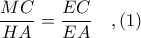
 , γιατί έχουν
, γιατί έχουν  και
και 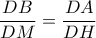 , έχουμε
, έχουμε 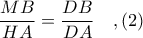
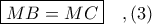 λόγω
λόγω 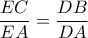
 και
και  .
.
 λόγω της ομοιότητας των τριγώνων
λόγω της ομοιότητας των τριγώνων  προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο
είναι εγγράψιμο 

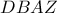 είναι εγγράψιμο
είναι εγγράψιμο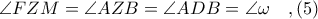
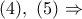
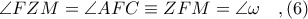
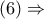
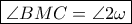 και το
και το  η ευθεία
η ευθεία  , ως παράλληλη προς την διχοτόμο της γωνίας
, ως παράλληλη προς την διχοτόμο της γωνίας 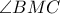 του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  , είναι κάθετη επί την
, είναι κάθετη επί την  .
. οι ευθείες
οι ευθείες  είναι ισογώνιες ως προς την γωνία
είναι ισογώνιες ως προς την γωνία  .
.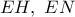 είναι ισογώνιες ως προς την γωνία
είναι ισογώνιες ως προς την γωνία  και οι ευθείες
και οι ευθείες  είναι ισογώνιες ως προς την γωνία
είναι ισογώνιες ως προς την γωνία  .
.
 είναι ισογώνια της
είναι ισογώνια της 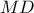 ως προς την γωνία
ως προς την γωνία  και η δια του σημείου
και η δια του σημείου  κάθετη ευθεία επί την
κάθετη ευθεία επί την  ως προς την γωνία
ως προς την γωνία  .
. τώρα, σύμφωνα πάλι με το
τώρα, σύμφωνα πάλι με το  και η δια του σημείου
και η δια του σημείου 

 και επειδή οι ευθείες
και επειδή οι ευθείες  ταυτίζονται, συμπεραίνεται ότι
ταυτίζονται, συμπεραίνεται ότι