 , ακτίνας
, ακτίνας  , κινείται σημείο
, κινείται σημείο  . Η εφαπτομένη του τόξου
. Η εφαπτομένη του τόξουστο
 , τέμνει τις προεκτάσεις των
, τέμνει τις προεκτάσεις των  στα σημεία
στα σημεία  αντίστοιχα και έστω
αντίστοιχα και έστω 
το μέσο του τμήματος
 . Υπολογίστε το ελάχιστο μήκος του τμήματος
. Υπολογίστε το ελάχιστο μήκος του τμήματος  .
.Συντονιστής: KAKABASBASILEIOS
 , ακτίνας
, ακτίνας  , κινείται σημείο
, κινείται σημείο  . Η εφαπτομένη του τόξου
. Η εφαπτομένη του τόξου , τέμνει τις προεκτάσεις των
, τέμνει τις προεκτάσεις των  στα σημεία
στα σημεία  αντίστοιχα και έστω
αντίστοιχα και έστω 
 . Υπολογίστε το ελάχιστο μήκος του τμήματος
. Υπολογίστε το ελάχιστο μήκος του τμήματος  .
. (στο 1ο τεταρτημόριο).
(στο 1ο τεταρτημόριο). , οπότε η εξίσωση της εφαπτομένης είναι η
, οπότε η εξίσωση της εφαπτομένης είναι η 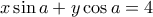 . Τότε φανερά είναι
. Τότε φανερά είναι 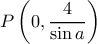 και
και 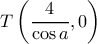 . Άρα είναι
. Άρα είναι 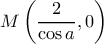 .
.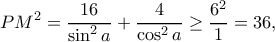 οπότε
οπότε 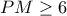 και η ισότητα ισχύει όταν
και η ισότητα ισχύει όταν 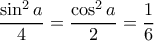 , δηλαδή όταν
, δηλαδή όταν  δηλαδή
δηλαδή 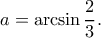
Αν
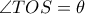 , τότε
, τότε  και
και 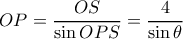 . Από Πυθαγόρειο
. Από Πυθαγόρειο  .
. , από όπου
, από όπου 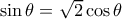 ή αλλιώς
ή αλλιώς 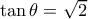 .
.  , είναι άμεσα από τις
, είναι άμεσα από τις 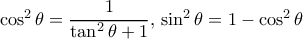
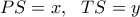 τότε:
τότε: 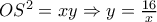
 και
και 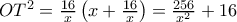
 οπότε
οπότε 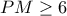 και το ίσον ισχύει όταν
και το ίσον ισχύει όταν 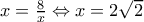
 ,
,  , και με τη βοήθεια της παραγώγου βρίσκουμε ότι έχει ελάχιστο για
, και με τη βοήθεια της παραγώγου βρίσκουμε ότι έχει ελάχιστο για  με τιμή
με τιμή  .
.

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες