Ολοκλήρωμα Riemann

TrItOs · #1

Έστω $f:[ a , b ] \rightarrow \mathbb{R}$ μια παραγωγίσιμη συνάρτηση ώστε η f'(x)

να είναι ολοκληρώσιμη κατά Riemann

στο

Θέτουμε
$\displaystyle{ a_{n} = \int\limits_{a}^{b} f(x) \text{ } dx - \frac{b-a}{n} \cdot \sum\limits_{k=1}^{n} f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \quad , \quad \forall n \in \mathbb{N} }$

Αποδείξτε ότι:
$\displaystyle{ \lim\limits_{n \to + \infty} \big( n \cdot a_{n} \big) = \frac{b-a}{2} \cdot \bigg( f(a) - f(b) \bigg) }$

ii)

Υπολογίστε το όριο:
$\displaystyle{ \lim\limits_{n \to + \infty} \bigg[ n \cdot \bigg( \frac{1^{k} + 2^{k} + 3^{k} + \cdots + (n-1)^{k} + n^{k}}{n^{k+1}} - \frac{1}{k+1} \bigg) \bigg] \quad , \quad \forall k \in \mathbb{N} }$

#2

TrItOs έγραψε: ↑
Δευ Σεπ 07, 2020 11:42 am
Έστω $f:[ a , b ] \rightarrow \mathbb{R}$ μια παραγωγίσιμη συνάρτηση ώστε η να είναι ολοκληρώσιμη κατά στο Θέτουμε
$\displaystyle{ a_{n} = \int\limits_{a}^{b} f(x) \text{ } dx - \frac{b-a}{n} \cdot \sum\limits_{k=1}^{n} f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \quad , \quad \forall n \in \mathbb{N} }$
Αποδείξτε ότι:
$\displaystyle{ \lim\limits_{n \to + \infty} \big( n \cdot a_{n} \big) = \frac{b-a}{2} \cdot \bigg( f(a) - f(b) \bigg) }$

Υπολογίστε το όριο:
$\displaystyle{ \lim\limits_{n \to + \infty} \bigg[ n \cdot \bigg( \frac{1^{k} + 2^{k} + 3^{k} + \cdots + (n-1)^{k} + n^{k}}{n^{k+1}} - \frac{1}{k+1} \bigg) \bigg] \quad , \quad \forall k \in \mathbb{N} }$

Επειδή είναι στάνταρ άσκηση που υπάρχει σε όλα τα βιβλία Ανάλυσης και επειδή η πληκτρολόγηση είναι επίπονη, θα δώσω μόνο υπόδειξη.

Πρώτα απ' 'ολα σου αρκεί

φραγμένη.

Χώρησε το ολοκλήρωμα σε άθροισμα άλλων, στα σημεία $a + k \cdot \frac{b-a}{n}$ . Σε κάθε ένα από αυτά το ολοκλήρωμα, από το ΘΜΤ, ισούται

με όρο της μορφής $f(\xi_k) \cdot \frac{b-a}{n}$ . Με τον αντίστοιχο όρο στο δοθέν άθροισμα εμφανίζονται όροι τύπου

$\displaystyle{\left ( f(\xi_k)- f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \right ) \cdot \frac{b-a}{n}}$

Τώρα Rolle στην πρώτη παρένθεση, και τα υπόλοιπα άμεσα.

Το ιι) είναι άμεση εφαρμογή του ι).

stranger · #3

Για το ii) παίρνουμε f(x)=x^k

, όπου $x \in [0,1]$ και χρησιμοποιώντας το i) παίρνουμε ότι το όριο είναι $\frac{1}{2}$ .

TrItOs · #4

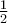Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm

TrItOs έγραψε: ↑
Δευ Σεπ 07, 2020 11:42 am
Έστω $f:[ a , b ] \rightarrow \mathbb{R}$ μια παραγωγίσιμη συνάρτηση ώστε η να είναι ολοκληρώσιμη κατά στο Θέτουμε
$\displaystyle{ a_{n} = \int\limits_{a}^{b} f(x) \text{ } dx - \frac{b-a}{n} \cdot \sum\limits_{k=1}^{n} f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \quad , \quad \forall n \in \mathbb{N} }$
Αποδείξτε ότι:
$\displaystyle{ \lim\limits_{n \to + \infty} \big( n \cdot a_{n} \big) = \frac{b-a}{2} \cdot \bigg( f(a) - f(b) \bigg) }$

Υπολογίστε το όριο:
$\displaystyle{ \lim\limits_{n \to + \infty} \bigg[ n \cdot \bigg( \frac{1^{k} + 2^{k} + 3^{k} + \cdots + (n-1)^{k} + n^{k}}{n^{k+1}} - \frac{1}{k+1} \bigg) \bigg] \quad , \quad \forall k \in \mathbb{N} }$
Επειδή είναι στάνταρ άσκηση που υπάρχει σε όλα τα βιβλία Ανάλυσης και επειδή η πληκτρολόγηση είναι επίπονη, θα δώσω μόνο υπόδειξη.

Πρώτα απ' 'ολα σου αρκεί φραγμένη.

Χώρησε το ολοκλήρωμα σε άθροισμα άλλων, στα σημεία $a + k \cdot \frac{b-a}{n}$ . Σε κάθε ένα από αυτά το ολοκλήρωμα, από το ΘΜΤ, ισούται

με όρο της μορφής $f(\xi_k) \cdot \frac{b-a}{n}$ . Με τον αντίστοιχο όρο στο δοθέν άθροισμα εμφανίζονται όροι τύπου

$\displaystyle{\left ( f(\xi_k)- f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \right ) \cdot \frac{b-a}{n}}$

Τώρα Rolle στην πρώτη παρένθεση, και τα υπόλοιπα άμεσα. (Δεν έχω καταλάβει πως θα εφαρμόσω το θεωρημα του Rolle )

Το ιι) είναι άμεση εφαρμογή του ι).

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #5

Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm

TrItOs έγραψε: ↑
Δευ Σεπ 07, 2020 11:42 am
Έστω $f:[ a , b ] \rightarrow \mathbb{R}$ μια παραγωγίσιμη συνάρτηση ώστε η να είναι ολοκληρώσιμη κατά στο Θέτουμε
$\displaystyle{ a_{n} = \int\limits_{a}^{b} f(x) \text{ } dx - \frac{b-a}{n} \cdot \sum\limits_{k=1}^{n} f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \quad , \quad \forall n \in \mathbb{N} }$
Αποδείξτε ότι:
$\displaystyle{ \lim\limits_{n \to + \infty} \big( n \cdot a_{n} \big) = \frac{b-a}{2} \cdot \bigg( f(a) - f(b) \bigg) }$

Υπολογίστε το όριο:
$\displaystyle{ \lim\limits_{n \to + \infty} \bigg[ n \cdot \bigg( \frac{1^{k} + 2^{k} + 3^{k} + \cdots + (n-1)^{k} + n^{k}}{n^{k+1}} - \frac{1}{k+1} \bigg) \bigg] \quad , \quad \forall k \in \mathbb{N} }$
Επειδή είναι στάνταρ άσκηση που υπάρχει σε όλα τα βιβλία Ανάλυσης και επειδή η πληκτρολόγηση είναι επίπονη, θα δώσω μόνο υπόδειξη.

Πρώτα απ' 'ολα σου αρκεί φραγμένη.

Χώρησε το ολοκλήρωμα σε άθροισμα άλλων, στα σημεία $a + k \cdot \frac{b-a}{n}$ . Σε κάθε ένα από αυτά το ολοκλήρωμα, από το ΘΜΤ, ισούται

με όρο της μορφής $f(\xi_k) \cdot \frac{b-a}{n}$ . Με τον αντίστοιχο όρο στο δοθέν άθροισμα εμφανίζονται όροι τύπου

$\displaystyle{\left ( f(\xi_k)- f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \right ) \cdot \frac{b-a}{n}}$

Τώρα Rolle στην πρώτη παρένθεση, και τα υπόλοιπα άμεσα.

Το ιι) είναι άμεση εφαρμογή του ι).

Μιχάλη δεν βλέπω πως μπορεί αυτό να φτάνει.

Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm
Πρώτα απ' 'ολα σου αρκεί φραγμένη.

Συμπλήρωμα.
Φτάνει αν χρησιμοποιήσουμε ολοκλήρωμα Lebesgue.

#6

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Σεπ 08, 2020 12:59 am

Μιχάλη δεν βλέπω πως μπορεί αυτό να φτάνει.
Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm
Πρώτα απ' 'ολα σου αρκεί φραγμένη.
Συμπλήρωμα.
Φτάνει αν χρησιμοποιήσουμε ολοκλήρωμα Lebesgue.

Σταύρο, δεν σε ξέχασα. Θα το κοιτάξω.

Αυτό τον καιρό έχω πολύ φόρτο εργασίας, ξενυχτάω, οπότε κοιτάω μόνο ... τα εύκολα. Τα δικά σου
είναι πάντα δύσκολα!

TrItOs · #7

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Σεπ 08, 2020 12:59 am

Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm

TrItOs έγραψε: ↑
Δευ Σεπ 07, 2020 11:42 am
Έστω $f:[ a , b ] \rightarrow \mathbb{R}$ μια παραγωγίσιμη συνάρτηση ώστε η να είναι ολοκληρώσιμη κατά στο Θέτουμε
$\displaystyle{ a_{n} = \int\limits_{a}^{b} f(x) \text{ } dx - \frac{b-a}{n} \cdot \sum\limits_{k=1}^{n} f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \quad , \quad \forall n \in \mathbb{N} }$
Αποδείξτε ότι:
$\displaystyle{ \lim\limits_{n \to + \infty} \big( n \cdot a_{n} \big) = \frac{b-a}{2} \cdot \bigg( f(a) - f(b) \bigg) }$

Υπολογίστε το όριο:
$\displaystyle{ \lim\limits_{n \to + \infty} \bigg[ n \cdot \bigg( \frac{1^{k} + 2^{k} + 3^{k} + \cdots + (n-1)^{k} + n^{k}}{n^{k+1}} - \frac{1}{k+1} \bigg) \bigg] \quad , \quad \forall k \in \mathbb{N} }$
Επειδή είναι στάνταρ άσκηση που υπάρχει σε όλα τα βιβλία Ανάλυσης και επειδή η πληκτρολόγηση είναι επίπονη, θα δώσω μόνο υπόδειξη.

Πρώτα απ' 'ολα σου αρκεί φραγμένη.

Χώρησε το ολοκλήρωμα σε άθροισμα άλλων, στα σημεία $a + k \cdot \frac{b-a}{n}$ . Σε κάθε ένα από αυτά το ολοκλήρωμα, από το ΘΜΤ, ισούται

με όρο της μορφής $f(\xi_k) \cdot \frac{b-a}{n}$ . Με τον αντίστοιχο όρο στο δοθέν άθροισμα εμφανίζονται όροι τύπου

$\displaystyle{\left ( f(\xi_k)- f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \right ) \cdot \frac{b-a}{n}}$

Τώρα Rolle στην πρώτη παρένθεση, και τα υπόλοιπα άμεσα.

$\rightarrow$ ( Πως επιλύεται το πρώτο ερώτημα του προβλήματος και πως ακριβλως εφαρμόζω το θεώρημα του Rolle ) $\leftarrow$

Το ιι) είναι άμεση εφαρμογή του ι).
Μιχάλη δεν βλέπω πως μπορεί αυτό να φτάνει.
Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm
Πρώτα απ' 'ολα σου αρκεί φραγμένη.
Συμπλήρωμα.
Φτάνει αν χρησιμοποιήσουμε ολοκλήρωμα Lebesgue.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #8

TrItOs έγραψε: ↑
Τετ Σεπ 09, 2020 2:24 pm

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Σεπ 08, 2020 12:59 am

Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm

TrItOs έγραψε: ↑
Δευ Σεπ 07, 2020 11:42 am
Έστω $f:[ a , b ] \rightarrow \mathbb{R}$ μια παραγωγίσιμη συνάρτηση ώστε η να είναι ολοκληρώσιμη κατά στο Θέτουμε
$\displaystyle{ a_{n} = \int\limits_{a}^{b} f(x) \text{ } dx - \frac{b-a}{n} \cdot \sum\limits_{k=1}^{n} f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \quad , \quad \forall n \in \mathbb{N} }$
Αποδείξτε ότι:
$\displaystyle{ \lim\limits_{n \to + \infty} \big( n \cdot a_{n} \big) = \frac{b-a}{2} \cdot \bigg( f(a) - f(b) \bigg) }$

Υπολογίστε το όριο:
$\displaystyle{ \lim\limits_{n \to + \infty} \bigg[ n \cdot \bigg( \frac{1^{k} + 2^{k} + 3^{k} + \cdots + (n-1)^{k} + n^{k}}{n^{k+1}} - \frac{1}{k+1} \bigg) \bigg] \quad , \quad \forall k \in \mathbb{N} }$
Επειδή είναι στάνταρ άσκηση που υπάρχει σε όλα τα βιβλία Ανάλυσης και επειδή η πληκτρολόγηση είναι επίπονη, θα δώσω μόνο υπόδειξη.

Πρώτα απ' 'ολα σου αρκεί φραγμένη.

Χώρησε το ολοκλήρωμα σε άθροισμα άλλων, στα σημεία $a + k \cdot \frac{b-a}{n}$ . Σε κάθε ένα από αυτά το ολοκλήρωμα, από το ΘΜΤ, ισούται

με όρο της μορφής $f(\xi_k) \cdot \frac{b-a}{n}$ . Με τον αντίστοιχο όρο στο δοθέν άθροισμα εμφανίζονται όροι τύπου

$\displaystyle{\left ( f(\xi_k)- f \bigg( a + k \cdot \frac{b-a}{n} \bigg) \right ) \cdot \frac{b-a}{n}}$

Τώρα Rolle στην πρώτη παρένθεση, και τα υπόλοιπα άμεσα.

$\rightarrow$ ( Πως επιλύεται το πρώτο ερώτημα του προβλήματος και πως ακριβλως εφαρμόζω το θεώρημα του Rolle ) $\leftarrow$

Το ιι) είναι άμεση εφαρμογή του ι).
Μιχάλη δεν βλέπω πως μπορεί αυτό να φτάνει.
Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm
Πρώτα απ' 'ολα σου αρκεί φραγμένη.
Συμπλήρωμα.
Φτάνει αν χρησιμοποιήσουμε ολοκλήρωμα Lebesgue.

Δεν καταλαβαίνω το νόημα της παράθεσης.
Ο Μιχάλης έχει υποσχεθεί να το δει.
Θα γράψω μετά από αυτόν.
Με την ευκαιρία έχεις λύση ;
Από που είναι η άσκηση -πρόταση ;

#9

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑
Τρί Σεπ 08, 2020 12:59 am
Μιχάλη δεν βλέπω πως μπορεί αυτό να φτάνει.
Mihalis_Lambrou έγραψε: ↑
Δευ Σεπ 07, 2020 3:31 pm
Πρώτα απ' 'ολα σου αρκεί φραγμένη.

.
Σταύρο, έχεις δίκιο. Δίνω λύση στο ερώτημα με την συνθήκη όπως δόθηκε αρχικά, όχι με την βελτίωση που πρότεινα.

Η αλήθεια είναι ότι δεν βλέπω γιατί ο TrItOs πιέζει για πλήρη λύση αφού αυτά που είχα γράψει είναι σχεδόν έτοιμη πλήρης λύση.
Θα μπορούσε να συνεχίσει μόνος του. Όπως και να είναι, αρχίζω από την αρχή αλλά κάνω μία μικρή παραλλαγή αυτών που έγραψα ήδη.

Χώρησε το ολοκλήρωμα σε άθροισμα άλλων, στα σημεία $a + k \cdot \frac{b-a}{n}$ . Σε κάθε ένα από αυτά έχουμε το ολοκλήρωμα του

$\displaystyle{f(x)- a - k \cdot \frac{b-a}{n}}$

Aπό Rolle, ισούται με το ολοκλήρωμα από $a + (k-1) \cdot \frac{b-a}{n}$ έως $a + k \cdot \frac{b-a}{n}$

με όρο της μορφής $(x- a - k \frac{b-a}{n}) f'(\xi_k)$ . Προσοχή, το μέσα είναι αρνητικός. Αν m_k, M_k

το κάτω και το άνω φράγμα της

στο συγκεκριιμένο διάστημα, το εν λόγω ολοκλήρωμα είναι μεταξύ του

$\displaystyle{ -M_k\int _{a + (k-1) \cdot \frac{b-a}{n} }^{a + k \cdot \frac{b-a}{n}} \left (x- a-k\cdot \frac{b-a}{n}\right ) dx}$ και του $\displaystyle{ -m_k\int _{a + (k-1) \cdot \frac{b-a}{n} }^{a + k \cdot \frac{b-a}{n}}\left ( x- a-k \cdot \frac{b-a}{n}\right ) dx}$

δηλαδή μεταξύ του $\displaystyle{ -\dfrac {1}{2} M_k \left ( \dfrac {b-a}{n}\right )^2}$ και του $\displaystyle{ -\dfrac {1}{2} m_k \left ( \dfrac {b-a}{n}\right )^2}$

Ποσθέτουμε και πολλαπλασιάζουμε επί

οπότε

$\displaystyle{ -\dfrac {1}{2} \dfrac {(b-a)^2}{n} \sum M_k \le na_n \le -\dfrac {1}{2} \dfrac {(b-a)^2}{n}\sum m_k }$

Τώρα, επειδή η

είναι ολοκληρώσιμη, έχουμε ότι από κριτήριο Riemann τα $\displaystyle{\dfrac {b-a}{n} \sum M_k }$ και $\displaystyle{\dfrac {b-a}{n} \sum m_k }$ τείνουν στο

$\displaystyle{\int _a^bf'(x)dx= f(b)-f(a)}$ .

To ζητούμενο είναι τώρα άμεσο.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #10

Ας το δείξουμε χωρίς η παράγωγος να είναι Riemann ολοκληρώσιμη αλλά απλώς φραγμένη.
Να σημειώσω ότι υπάρχει συνεχής συνάρτηση με φραγμένη παράγωγο της οποίας η παράγωγος δεν είναι Riemann ολοκληρώσιμη.
Βλέπε ασκηση 18-112 στο
Απειροστικός Λογισμός Τόμος ΙΙ
Σ.Νεγρεπόντης Σ.Γιωτόπουλος Ε.Γιαννακούλιας.

Στο
viewtopic.php?f=9&t=65830&p=318764#p318764
βλέπουμε ότι αν η παράγωγος είναι φραγμένη τότε είναι Lebesgue ολοκληρώσιμη και ισχύει
για αυτήν το Θεμελιώδες θεώρημα του Απειροστικού.

Θέτουμε $h=\frac{b-a}{n},x_{k}=a+kh,k=0,1,...n$
Είναι
$\displaystyle a_{n}=\int_{a}^{b}f(x)dx-h\sum_{k=1}^{n}f(x_k)=\sum_{k=1}^{n}\int_{x_{k-1}}^{x_k}(f(x)-f(x_k))dx$

Αλλά
$\displaystyle \int_{x_{k-1}}^{x_k}(f(x)-f(x_k))dx=\int_{x_{k-1}}^{x_k}(f(x)-f(x_k))(x-x_{k-1})'dx$
$\displaystyle =-\int_{x_{k-1}}^{x_k}f'(x)(x-x_{k-1})dx$

Αμεσα προκύπτει ότι
$\displaystyle na_n=-\frac{b-a}{h}\sum_{k=1}^{n} \int_{x_{k-1}}^{x_k}f'(x)(x-x_{k-1})dx$ (1)

Χρησιμοποιώντας ότι
$\displaystyle f(b)-f(a)=\int_{a}^{b}f'(x)dx$
σπάζοντας το τελευταίο ολοκλήρωμα η (1) δίνει

$\displaystyle na_n+\frac{b-a}{2}(f(b)-f(a))=\frac{b-a}{2}\sum_{k=1}^{n} (\int_{x_{k-1}}^{x_k}f'(x)dx-\frac{2}{h}\int_{x_{k-1}}^{x_k}f'(x)(x-x_{k-1})dx)$ (2)

είναι
$\displaystyle \int_{x_{k-1}}^{x_k}f'(x)dx-\frac{2}{h}\int_{x_{k-1}}^{x_k}f'(x)(x-x_{k-1})dx=$
$\displaystyle \frac{1}{h}(\int_{x_{k-1}}^{x_k}f'(x)(x_k-x_{k-1})dx-\int_{x_{k-1}}^{x_k}f'(x)(2x-2x_{k-1})dx)$
$\displaystyle =\frac{2}{h}\int_{x_{k-1}}^{x_k}f'(x)(\frac{x_k+x_{k-1}}{2}-x)dx$

Επειδή
$\displaystyle \int_{x_{k-1}}^{x_k}(\frac{x_k+x_{k-1}}{2}-x)dx=0$

παίρνουμε ότι
$\displaystyle \frac{2}{h}\int_{x_{k-1}}^{x_k}f'(x)(\frac{x_k+x_{k-1}}{2}-x)dx$
$\displaystyle =\frac{2}{h}\int_{x_{k-1}}^{x_k}(f'(x)-f'(\frac{x_k+x_{k-1}}{2})(\frac{x_k+x_{k-1}}{2}-x)dx$

Αν

είναι το απόλυτο φράγμα της παραγώγου ,κάνουμε ένα ΘΜΤ βλέπουμε ότι η απόλυτη τιμή του τελευταίου ολοκληρώματος δεν ξεπερνάει το

$\displaystyle \frac{2}{h}M\int_{x_{k-1}}^{x_k}(x-\frac{x_k+x_{k-1}}{2})^{2}dx=\frac{2}{h}Mc(x_k-x_{k-1})^{3}=CMh^{2}$

οπου c,C

απόλυτες υπολογίσημες σταθερές .

Ετσι η απόλυτη τιμή του πρώτου μέλους της (2) δεν ξεπερνάει

$\displaystyle\frac{b-a}{2} CMnh^2=\frac{1}{2}CM(b-a)^2h$

προφανώς το τελευταίο πάει στο

όταν $n\rightarrow \infty$
και έχουμε την ολοκλήρωση της απόδειξης.

Το αποτέλεσμα έχει άμεση εφαρμογή στην Αριθμητική Ανάλυση για προσεγγιστική τιμή ολοκληρώματος
δίνοντας και εκτίμηση σφάλματος.
Εγω τουλάχιστον δεν το γνώριζα.

Ολοκλήρωμα Riemann

Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Re: Ολοκλήρωμα Riemann

Μέλη σε σύνδεση