 της προέκτασης της διαμέτρου
της προέκτασης της διαμέτρου  ενός ημικυκλίου , φέρουμε το εφαπτόμενο τμήμα
ενός ημικυκλίου , φέρουμε το εφαπτόμενο τμήμα 
και την διχοτόμο της
 , η οποία τέμνει το τόξο σε δύο σημεία και ονομάζω
, η οποία τέμνει το τόξο σε δύο σημεία και ονομάζω  το πλησιέστερο στο
το πλησιέστερο στο  .
.Αν
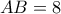 και
και  , υπολογίστε το ακριβές μήκος της χορδής
, υπολογίστε το ακριβές μήκος της χορδής 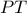 . Σημαντική σημείωση :
. Σημαντική σημείωση : Είναι κυρίως άσκηση Άλγεβρας , γι' αυτό στην λύση σας να φαίνεται η υπερπήδηση των αλγεβρικών εμποδίων

 η προβολή του
η προβολή του  στην
στην  Τότε
Τότε  και
και 


 και με Π. Θ στο
και με Π. Θ στο 



 (
( )
) το μέσο του
το μέσο του  μισό του
μισό του  ,
,






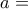



 και η
και η  είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  η προβολή του
η προβολή του  το κέντρο του ημικυκλίου. Θέτω
το κέντρο του ημικυκλίου. Θέτω  και άρα
και άρα 
 έχω :
έχω :  . Αν
. Αν  έχω:
έχω: οπότε :
οπότε : 
 . Έξω απ αυτό γράφω νέο ημικύκλιο διαμέτρου
. Έξω απ αυτό γράφω νέο ημικύκλιο διαμέτρου  και «υψώνω» κάθετη,
και «υψώνω» κάθετη,  ,στο
,στο  τέμνει το μικρό ημικύκλιο στο
τέμνει το μικρό ημικύκλιο στο  . Ας είναι
. Ας είναι  το μέσο του
το μέσο του  .
. . Η κάθετη στο
. Η κάθετη στο 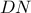 τέμνει αυτό το τρίτο ημικύκλιο στο
τέμνει αυτό το τρίτο ημικύκλιο στο  ,
, τέμνει την
τέμνει την  στο
στο