lagrange υπό συνθήκη

Sissy · #1

Καλησπέρα σας,θέλω μια βοήθεια στην παρακάτω άσκηση. Έχω βρει τις παραγώγους αλλά όταν πάω να λύσω τις εξισώσεις δεν μπορώ να βρω τα x,y,λ.
$f(x,y)=x^{4} + 4x^{2}y^{2} + y^{4} -4x^{3} - 4y^{3}$
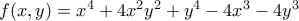
όταν η f ορίζεται στον κλειστό τόπο D που περικλείεται από τα ευθύγραμμα τμήματα ΟΑ, ΟΒ και το τόξο
AB= ${(x,y)\epsilon \mathbb{R}^{2} : x^{2} + y^{2} =4 , x,y \geq 0}$
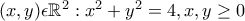
όπου Ο (0,0)

Α

Β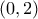

Εγώ βρίσκω τις εξής εξισώσεις:
$4x^{3}+8xy^{2}-12x^{2}+2\lambda x=0$

$4y^{3}+8yx^{2}-12y^{2}+2\lambda y=0$

$x^{2} + y^{2}= 4$

Λύνω τις 2 εξισώσεις ως προς λ και και τις παίρνω ίσες, ώστε να βρω τα x,y .
Αλλά δεν ξέρω αν είναι σωστός ο τρόπος μου.

Summand · #2

Καλησπέρα σου!

Από αυτό που βλέπω καταλαβαίνω ότι πας να μελετήσεις τα ακρότατα υπό συνθήκη με την μέθοδο πολλαπλασιαστών Lagrange, όμως για να μην κάνουμε εικασίες, θα μπορούσες να μας δώσεις την πλήρη εκφώνηση της άσκησης;

#3

$\begin{aligned} \left\{\begin{array}{r} 4x^3+8xy^2-12x^2-2\lambda x = 0\\ 4y^3+8x^2y-12y^2-2\lambda y = 0\\ x^2+y^2 = 4 \end{array} \right\}\quad&\Rightarrow\quad\left\{\begin{array}{r} 4(x-y)\big(\underbrace{x^2+y^2}\limits_{=4}-xy-3x-3y-\frac{1}{2}\lambda\big) = 0\\ 4y^3+8x^2y-12y^2-2\lambda y = 0\\ x^2+y^2 = 4 \end{array} \right\}\\ &\Rightarrow\quad\ldots \end{aligned}$

Από όπου προκύπτουν οι λύσεις του συστήματος.

Sissy · #4

Summand έγραψε: ↑
Τετ Ιούλ 29, 2020 4:14 am
Καλησπέρα σου!

Από αυτό που βλέπω καταλαβαίνω ότι πας να μελετήσεις τα ακρότατα υπό συνθήκη με την μέθοδο πολλαπλασιαστών Lagrange, όμως για να μην κάνουμε εικασίες, θα μπορούσες να μας δώσεις την πλήρη εκφώνηση της άσκησης;

Ναι συγνώμη έχετε δίκιο, παράλειψη μου. Θέλει να βρούμε το μέγιστο και το ελάχιστο από την συνάρτηση που δίνω πιο πάνω.
Απλά έχω μια δυσκολία στην λύση των εξισώσεων, ώστε να μπορέσω μετά να πάρω τα σημεία και να ελέγξω αν είναι μέγιστα ή ελάχιστα.

Sissy · #5

grigkost έγραψε: ↑
Τετ Ιούλ 29, 2020 6:50 am
$\begin{aligned} \left\{\begin{array}{r} 4x^3+8xy^2-12x^2-2\lambda x = 0\\ 4y^3+8x^2y-12y^2-2\lambda y = 0\\ x^2+y^2 = 4 \end{array} \right\}\quad&\Rightarrow\quad\left\{\begin{array}{r} 4(x-y)\big(\underbrace{x^2+y^2}\limits_{=4}-xy-3x-3y-\frac{1}{2}\lambda\big) = 0\\ 4y^3+8x^2y-12y^2-2\lambda y = 0\\ x^2+y^2 = 4 \end{array} \right\}\\ &\Rightarrow\quad\ldots \end{aligned}$

Από όπου προκύπτουν οι λύσεις του συστήματος.

Καλημέρα, έτσι το έκανα και εγώ ... και πήρα μετά 2 περιπτώσεις.
$\chi =\psi$
όπου το έκανα αντικατάσταση στις άλλες και βρήκα $\chi =\sqrt{2} , \psi =\sqrt{2}, \lambda =12-6\sqrt{2}$
και στην δεύτερη περίπτωση
$4-\chi \psi -3\chi -3\psi -\frac{1}{2}\lambda =0$
την λύνω ως προς λ ώστε να το αντικαταστήσω στην άλλη εξίσωση, και εκεί δεν μπορώ να συνεχίσω ....
Κάπου μάλλον μπερδεύομαι.

Al.Koutsouridis · #6

Sissy έγραψε: ↑
Τετ Ιούλ 29, 2020 11:04 am

grigkost έγραψε: ↑
Τετ Ιούλ 29, 2020 6:50 am
$\begin{aligned} \left\{\begin{array}{r} 4x^3+8xy^2-12x^2-2\lambda x = 0\\ 4y^3+8x^2y-12y^2-2\lambda y = 0\\ x^2+y^2 = 4 \end{array} \right\}\quad&\Rightarrow\quad\left\{\begin{array}{r} 4(x-y)\big(\underbrace{x^2+y^2}\limits_{=4}-xy-3x-3y-\frac{1}{2}\lambda\big) = 0\\ 4y^3+8x^2y-12y^2-2\lambda y = 0\\ x^2+y^2 = 4 \end{array} \right\}\\ &\Rightarrow\quad\ldots \end{aligned}$

Από όπου προκύπτουν οι λύσεις του συστήματος.
Καλημέρα, έτσι το έκανα και εγώ ... και πήρα μετά 2 περιπτώσεις.
$\chi =\psi$
όπου το έκανα αντικατάσταση στις άλλες και βρήκα $\chi =\sqrt{2} , \psi =\sqrt{2}, \lambda =12-6\sqrt{2}$
και στην δεύτερη περίπτωση
$4-\chi \psi -3\chi -3\psi -\frac{1}{2}\lambda =0$
την λύνω ως προς λ ώστε να το αντικαταστήσω στην άλλη εξίσωση, και εκεί δεν μπορώ να συνεχίσω ....
Κάπου μάλλον μπερδεύομαι.

Θεώρησε το αρχικό σύστημα

$\begin{aligned} \left\{\begin{array}{r} 4x^3+8xy^2-12x^2-2\lambda x = 0\\ 4y^3+8x^2y-12y^2-2\lambda y = 0\\ x^2+y^2 = 4 \end{array} \right\} \end{aligned}$

και μελέτα το για $x \neq y$ και $x,y \neq 0$ . Δηλαδή διαίρεσε με

και

αντίστοιχα τις πρώτες δυο εξισώσεις για να απλοποιθούν λίγο. Ύστερα σχημάτισε δυο νέες εξισώσεις με προσθαφαίρεση αυτών των δυο. Προκύπτει ένα νέο σύστημα, το οποίο νομίζω μπορεί να λύθεί...

Sissy · #7

Σας ευχαριστώ όλους για την βοήθεια , το βρήκα!!!

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #8

Η πιο εύκολη λύση στο παραπάνω πρόβλημα είναι η εξής:
Θέτουμε
$x=2\cos \theta ,y=2\sin \theta ,0\leq \theta \leq \frac{\pi }{2}$

η συνάρτηση γίνεται

$16+2^5((\cos \theta )^{2}(\sin \theta )^{2})-(\cos \theta )^{3}-(\sin \theta )^{3})$

εύκολα με παραγώγους βλέπουμε ότι έχει ακρότατα στα

$\theta =\frac{\pi }{2},\frac{\pi }{4},0$
κλπ

lagrange υπό συνθήκη

lagrange υπό συνθήκη

Re: lagrange υπό συνθήκη

Re: lagrange υπό συνθήκη

Re: lagrange υπό συνθήκη

Re: lagrange υπό συνθήκη

Re: lagrange υπό συνθήκη

Re: lagrange υπό συνθήκη

Re: lagrange υπό συνθήκη

Μέλη σε σύνδεση