 , για κάθε μια από τις οποίες η εξίσωση
, για κάθε μια από τις οποίες η εξίσωση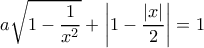
έχει ακριβώς δυο διαφορετικές ρίζες.
Συντονιστής: KAKABASBASILEIOS
 , για κάθε μια από τις οποίες η εξίσωση
, για κάθε μια από τις οποίες η εξίσωση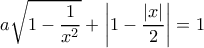
ΕίναιAl.Koutsouridis έγραψε: ↑Κυρ Ιουν 28, 2020 3:44 pmΝα βρείτε όλες τις τιμές της παραμέτρου, για κάθε μια από τις οποίες η εξίσωση
έχει ακριβώς δυο διαφορετικές ρίζες.

![(-\infty,-1]\cup [1,+\infty). (-\infty,-1]\cup [1,+\infty).](/forum/ext/geomar/texintegr/latexrender/pictures/60f725654bb6b783efe42503e00d3394.png) Παρατηρούμε ότι αν ο
Παρατηρούμε ότι αν ο  είναι ρίζα της εξίσωσης τότε
είναι ρίζα της εξίσωσης τότε  θα είναι. Επομένως μπορούμε να δουλέψουμε στο
θα είναι. Επομένως μπορούμε να δουλέψουμε στο  και να βρούμε τα
και να βρούμε τα  ώστε
ώστε  ο αριθμός
ο αριθμός  δεν είναι ρίζα της εξίσωσης.
δεν είναι ρίζα της εξίσωσης. 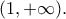 Θέτουμε
Θέτουμε  (1-1 μετασχηματισμός) και θα ισχύει τότε ότι
(1-1 μετασχηματισμός) και θα ισχύει τότε ότι 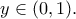 H εξίσωση παίρνει την μορφή
H εξίσωση παίρνει την μορφή 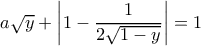 και πετώντας τα
και πετώντας τα ![a\sqrt{y}+ 1-\dfrac{1}{2\sqrt{1-y}} =1,y\in(0,\dfrac{3}{4}]\Leftrightarrow \dfrac{1}{2\sqrt{y(1-y)}}=a,y\in(0,\dfrac{3}{4}] a\sqrt{y}+ 1-\dfrac{1}{2\sqrt{1-y}} =1,y\in(0,\dfrac{3}{4}]\Leftrightarrow \dfrac{1}{2\sqrt{y(1-y)}}=a,y\in(0,\dfrac{3}{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/2fe42f1fec90f4cfe533a0350557e8c2.png)
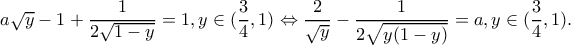
![f(y)=\left\{\begin{matrix} \dfrac{1}{2\sqrt{y(1-y)}}, &y\in(0,\frac{3}{4}] \\ \dfrac{2}{\sqrt{y}}-\dfrac{1}{2\sqrt{y(1-y)}}, &y\in(\frac{3}{4},1) \end{matrix}\right., f(y)=\left\{\begin{matrix} \dfrac{1}{2\sqrt{y(1-y)}}, &y\in(0,\frac{3}{4}] \\ \dfrac{2}{\sqrt{y}}-\dfrac{1}{2\sqrt{y(1-y)}}, &y\in(\frac{3}{4},1) \end{matrix}\right.,](/forum/ext/geomar/texintegr/latexrender/pictures/1ed7e97d4e9cdcb79db81d4d989ee844.png)
![y\in(0,\frac{3}{4}] y\in(0,\frac{3}{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/14864e90c45714a59544b2d51adb17a0.png) έχουμε ότι το
έχουμε ότι το 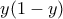 αυξάνει στο
αυξάνει στο ![[0,\frac{1}{2}] [0,\frac{1}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/6f5d1434932730c96a74db6c217a5e86.png) και μειώνεται στο
και μειώνεται στο ![[\frac{1}{2},\frac{3}{4}]. [\frac{1}{2},\frac{3}{4}].](/forum/ext/geomar/texintegr/latexrender/pictures/80a469c2920164cd0f7f25c78b27582d.png)
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![(0,\frac{1}{2}] (0,\frac{1}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/9915d06b2bcd9324f58678de1336fc78.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο ![[\frac{1}{2},\frac{3}{4}]. [\frac{1}{2},\frac{3}{4}].](/forum/ext/geomar/texintegr/latexrender/pictures/80a469c2920164cd0f7f25c78b27582d.png)
![y\in(0,\frac{3}{4}] y\in(0,\frac{3}{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/14864e90c45714a59544b2d51adb17a0.png) , είναι το
, είναι το ![[f(\frac{1}{2}),\lim_{y\rightarrow 0}f(y))\cup [f(\frac{1}{2}),f(\frac{3}{4})]=[1,+\infty)\cup [1,\frac{2}{\sqrt{3}}]=[1,+\infty). [f(\frac{1}{2}),\lim_{y\rightarrow 0}f(y))\cup [f(\frac{1}{2}),f(\frac{3}{4})]=[1,+\infty)\cup [1,\frac{2}{\sqrt{3}}]=[1,+\infty).](/forum/ext/geomar/texintegr/latexrender/pictures/71be1b9267321998623a868636f2f49a.png)
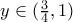 η
η  είναι γνησίως φθίνουσα αφού
είναι γνησίως φθίνουσα αφού 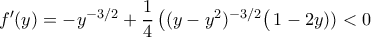
 , είναι το
, είναι το 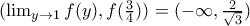 .
. είναι όλοι οι αριθμοί του
είναι όλοι οι αριθμοί του 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες