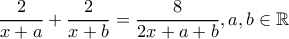
β) Λύστε την εξίσωση :

Σημείωση : Η άσκηση απευθύνεται σε μαθητές της Α' Λυκείου . Παρακαλείται λοιπόν ο λύτης
να αναρτήσει λύση λεπτομερή , σαν αυτή δηλαδή που θα προτείναμε να γράψει ο μαθητής .
Συντονιστής: stranton
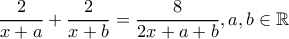

 εκτός από
εκτός από  .
. , οπότε η εξίσωση ορίζεται για
, οπότε η εξίσωση ορίζεται για 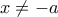 και είναι η
και είναι η 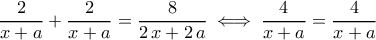 αόριστη δηλαδή εκτός του
αόριστη δηλαδή εκτός του  .
. . Έχουμε,
. Έχουμε, ![\begin{aligned}\dfrac{2}{x+a}+\dfrac{2}{x+b}=\dfrac{8}{2\,x+a+b}&\iff \dfrac{2\,(x+b)+2\,(x+a)}{(x+a)\,(x+b)}=\dfrac{8}{(x+a)+(x+b)}\\&\iff 2\,\left[(x+a)+(x+b)\right]^2=8\,(x+a)\,(x+b)\\&\iff 2\,(x+a)^2+2\,(x+b)^2+4\,(x+a)\,(x+b)-8\,(x+a)\,(x+b)=0\\&\iff 2\,(x+a)^2+2\,(x+b)^2-4\,(x+a)\,(x+b)=0\\&\iff 2\,[(x+a)-(x+b)]^2=0\\&\iff 0\,x=a-b \end{aligned} \begin{aligned}\dfrac{2}{x+a}+\dfrac{2}{x+b}=\dfrac{8}{2\,x+a+b}&\iff \dfrac{2\,(x+b)+2\,(x+a)}{(x+a)\,(x+b)}=\dfrac{8}{(x+a)+(x+b)}\\&\iff 2\,\left[(x+a)+(x+b)\right]^2=8\,(x+a)\,(x+b)\\&\iff 2\,(x+a)^2+2\,(x+b)^2+4\,(x+a)\,(x+b)-8\,(x+a)\,(x+b)=0\\&\iff 2\,(x+a)^2+2\,(x+b)^2-4\,(x+a)\,(x+b)=0\\&\iff 2\,[(x+a)-(x+b)]^2=0\\&\iff 0\,x=a-b \end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/60a52578ce58223489a360c5fb3454cd.png)
 εκτός των
εκτός των  .
. ![2\,[(x+a)+(x+b)]^2=9\,(x+a)\,(x+b) 2\,[(x+a)+(x+b)]^2=9\,(x+a)\,(x+b)](/forum/ext/geomar/texintegr/latexrender/pictures/71d2106f3b6343514d8f23c1cdc6512b.png) .
.  (με σύνολο ορισμού για
(με σύνολο ορισμού για 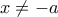 ) τότε έχουμε την εξίσωση
) τότε έχουμε την εξίσωση 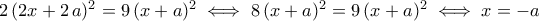 , απορρίπτεται.
, απορρίπτεται. , τότε η εξίσωση γίνεται
, τότε η εξίσωση γίνεται 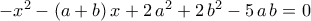 . Υπολογίζουμε τη διακρίνουσα που είναι
. Υπολογίζουμε τη διακρίνουσα που είναι  , και άρα οι ρίζες είναι
, και άρα οι ρίζες είναι 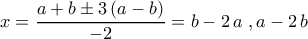 (δεκτές και οι 2 διότι καμία από αυτές δεν ισούται με κάποιο από τα
(δεκτές και οι 2 διότι καμία από αυτές δεν ισούται με κάποιο από τα  )
) με τους περιορισμούς
με τους περιορισμούς 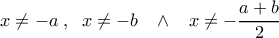

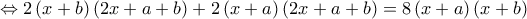

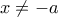 , αν και μόνο αν
, αν και μόνο αν  ,
, είναι αδύνατη.
είναι αδύνατη. με τους περιορισμούς
με τους περιορισμούς 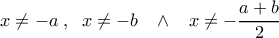
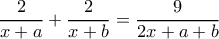
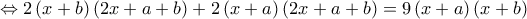
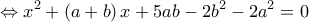
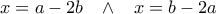
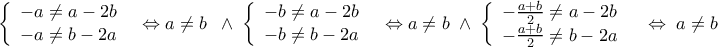
 η εξίσωση είναι αδύνατη, ενώ αν
η εξίσωση είναι αδύνατη, ενώ αν  , έχει λύσεις της μορφής:
, έχει λύσεις της μορφής: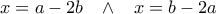 ,
, 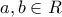 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες