Doloros έγραψε: ↑Τρί Απρ 28, 2020 12:25 pm
β) Δείξετε ότι η εξίσωση:

παριστάνει όλους τους κύκλους που διέρχονται από τα σημεία :
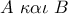
Μου τράβηξε την προσοχή το β) γιατί έχει ωραία λύση πέρα από την παραδοσιακή. Η λύση αυτή ερμηνεύει καλύτερα τα

και

στην ζητούμενη εξίσωση.
1) Παραδοσιακή: Το μέσον του

είναι το

οπότε η μεσοκάθετος του

είναι ...

. To κέντρο του τυχαίου κύκλου βρίσκεται στην μεσοκάθετο άρα είναι της μορφής

, οπότε εύκολα βρίσκουμε την εξίσωση του κύκλου από το κέντρο του και την ακτίνα του

. To αφήνω ως άμεσο και διότι
.
σίγουρα θα κάνω λάθος τις πράξεις την πρώτη φορά
2) Καλύτερα: Αν

τυχαίο σημείο του κύκλου, τότε η γωνία

είναι σταθερή. Δεδομένου ότι οι

έχουν κλίσεις

, αντίστοιχα, ο τύπος της μεταξύ τους γωνίας δίνει

ισοδύναμα

που είναι ισοδύναμο με το ζητούμενο (πάρε

) δεδομένου ότι ο αριθμητής είναι


 είναι :
είναι : 

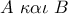
 κι εφάπτονται της ευθείας
κι εφάπτονται της ευθείας  , με εξίσωση :
, με εξίσωση :  .
.
 και
και 
 και
και  στην ζητούμενη εξίσωση.
στην ζητούμενη εξίσωση.  οπότε η μεσοκάθετος του
οπότε η μεσοκάθετος του  . To κέντρο του τυχαίου κύκλου βρίσκεται στην μεσοκάθετο άρα είναι της μορφής
. To κέντρο του τυχαίου κύκλου βρίσκεται στην μεσοκάθετο άρα είναι της μορφής  , οπότε εύκολα βρίσκουμε την εξίσωση του κύκλου από το κέντρο του και την ακτίνα του
, οπότε εύκολα βρίσκουμε την εξίσωση του κύκλου από το κέντρο του και την ακτίνα του  . To αφήνω ως άμεσο και διότι
. To αφήνω ως άμεσο και διότι  τυχαίο σημείο του κύκλου, τότε η γωνία
τυχαίο σημείο του κύκλου, τότε η γωνία  είναι σταθερή. Δεδομένου ότι οι
είναι σταθερή. Δεδομένου ότι οι  έχουν κλίσεις
έχουν κλίσεις  , αντίστοιχα, ο τύπος της μεταξύ τους γωνίας δίνει
, αντίστοιχα, ο τύπος της μεταξύ τους γωνίας δίνει  ισοδύναμα
ισοδύναμα  που είναι ισοδύναμο με το ζητούμενο (πάρε
που είναι ισοδύναμο με το ζητούμενο (πάρε  ) δεδομένου ότι ο αριθμητής είναι
) δεδομένου ότι ο αριθμητής είναι 
 και παριστάνει κύκλο
και παριστάνει κύκλο  και ακτίνα
και ακτίνα  Αφού οι κύκλοι εφάπτονται στην ευθεία
Αφού οι κύκλοι εφάπτονται στην ευθεία  θα είναι
θα είναι 
 ή
ή  απ' όπου παίρνουμε δύο κύκλους
απ' όπου παίρνουμε δύο κύκλους  με εξισώσεις:
με εξισώσεις:  και
και 