 με διευθετούσα την έλικα
με διευθετούσα την έλικα ![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείο
 της
της  , η τομή της
, η τομή της  με το κάθετο στην
με το κάθετο στην  επίπεδο είναι κύκλος με κέντρο το
επίπεδο είναι κύκλος με κέντρο το  και ακτίνα
και ακτίνα  .
. Να βρεθεί μια παραμετρική παράσταση της επιφάνειας
 και να υπολογισθεί το εμβαδόν της
και να υπολογισθεί το εμβαδόν της  .
. Συντονιστής: matha
 με διευθετούσα την έλικα
με διευθετούσα την έλικα ![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
 της
της  , η τομή της
, η τομή της  με το κάθετο στην
με το κάθετο στην  επίπεδο είναι κύκλος με κέντρο το
επίπεδο είναι κύκλος με κέντρο το  και ακτίνα
και ακτίνα  .
.  και να υπολογισθεί το εμβαδόν της
και να υπολογισθεί το εμβαδόν της  .
. 
να συμπληρώσω ότι ζητείται το εμβαδόν
 με απλό τρόπο, χωρίς να κάνουμε ολοκλήρωση. Ίσως αυτό έχει κατά νου ο Γρηγόρης...
με απλό τρόπο, χωρίς να κάνουμε ολοκλήρωση. Ίσως αυτό έχει κατά νου ο Γρηγόρης...Γρηγόρη καλημέρα και Χρόνια Πολλά από τα Γρεβενά...grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
(Συνέχεια...)grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
 του κύκλου
του κύκλου  .
.  είναι ένα τυχαίο σημείο της έλικας, τότε στο σημείο αυτό θεωρούμε,
είναι ένα τυχαίο σημείο της έλικας, τότε στο σημείο αυτό θεωρούμε, 
 είναι μοναδιαία και είναι αντίστοιχα
είναι μοναδιαία και είναι αντίστοιχα 

 είναι η γωνία που σχηματίζει το τμήμα
είναι η γωνία που σχηματίζει το τμήμα  με το διάνυσμα
με το διάνυσμα  της πρώτης καθέτου.
της πρώτης καθέτου. 




Το πρόβλημα είναι αν υπάρχει τέτοια επιφάνεια.grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
helicoid_surf.png
 είναι ''μεγάλο'' υπάρχει πρόβλημα.
είναι ''μεγάλο'' υπάρχει πρόβλημα. ''μικρό''
''μικρό'' έχει σχέση με την καμπυλότητα
έχει σχέση με την καμπυλότητα  με διευθετούσα την καμπύλη
με διευθετούσα την καμπύλη  με
με 
 της
της  , η τομή της
, η τομή της  με το κάθετο στην
με το κάθετο στην  επίπεδο είναι κύκλος με κέντρο το
επίπεδο είναι κύκλος με κέντρο το  και ακτίνα
και ακτίνα  .
.  και να υπολογισθεί το εμβαδόν της
και να υπολογισθεί το εμβαδόν της  .
. είναι ένα πεπερασμένο διάστημα των πραγματικών)
είναι ένα πεπερασμένο διάστημα των πραγματικών) είναι τέτοιο ώστε οι κύκλοι δεν τέμνονται.
είναι τέτοιο ώστε οι κύκλοι δεν τέμνονται.
 είναι το μήκος της καμπύλης.Υπολογίζεται χωρίζοντας σε μικρά κομμάτια και υπολογίζοντας
είναι το μήκος της καμπύλης.Υπολογίζεται χωρίζοντας σε μικρά κομμάτια και υπολογίζοντας  είναι το εφαπτόμενο ,πρώτο κάθετο ,δεύτερο κάθετο της καμπύλης στο
είναι το εφαπτόμενο ,πρώτο κάθετο ,δεύτερο κάθετο της καμπύλης στο  τότε ο κύκλος βρίσκεται στο επίπεδο που ορίζουν τα
τότε ο κύκλος βρίσκεται στο επίπεδο που ορίζουν τα  μετατοπισμένος στο
μετατοπισμένος στο  .
.
 είναι τα εσωτερικά σημεία του
είναι τα εσωτερικά σημεία του 
 (1)
(1) (2)
(2) και
και  είναι η καμπυλότητα και η στρέψη της καμπύλης τότε
είναι η καμπυλότητα και η στρέψη της καμπύλης τότε 
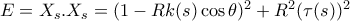


 (3)
(3)

 .
.
 είναι
είναι 

Αυτό που είχα κατά νου είναι η πολύ γενικότερη περίπτωση που παρουσίασε ο Σταύρος στην αμέσως προηγούμενη δημοσίευση. Να σημειωθεί ότι πρόκειται για σημαντική γενίκευση αφού η διευθετούσαMihalis_Lambrou έγραψε: ↑Κυρ Απρ 19, 2020 10:49 pm...να συμπληρώσω ότι ζητείται το εμβαδόνμε απλό τρόπο, χωρίς να κάνουμε ολοκλήρωση. Ίσως αυτό έχει κατά νου ο Γρηγόρης...
 μπορεί να είναι οποιαδήποτε κανονική καμπύλη για την οποία πρέπει να ισχύει
μπορεί να είναι οποιαδήποτε κανονική καμπύλη για την οποία πρέπει να ισχύει  , όπου
, όπου  η καμπυλότητα της
η καμπυλότητα της  αν έχουμε μια φυσική παραμετρικοποίησή της.
αν έχουμε μια φυσική παραμετρικοποίησή της.
Καλημέρα από Γρεβενά ...ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Απρ 25, 2020 11:15 pmΤο πρόβλημα είναι αν υπάρχει τέτοια επιφάνεια.grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
helicoid_surf.png
Δηλαδή οι κύκλοι να μην τέμνονται.(1)
Είναι σαφές ότι αν τοείναι ''μεγάλο'' υπάρχει πρόβλημα.
Θα φανεί και από την απόδειξη που θα κάνω παρακάτω.
Νομίζω ότι μπορεί να αποδειχθεί η ύπαρξη της επιφάνειας για''μικρό''
αλλά θα έχει πολύ φασαρία.
Η καμπύλη που είναι οδηγός της επιφάνειας μπορεί να είναι οποιαδήποτε .(2)
Τότε το πόσο μεγάλο μπορούμε να πάρουμε τοέχει σχέση με την καμπυλότητα
της καμπύλης.
........................................................
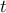 κινήθηκε στο διάστημα
κινήθηκε στο διάστημα ![\displaystyle{[0,8 \pi]} \displaystyle{[0,8 \pi]}](/forum/ext/geomar/texintegr/latexrender/pictures/97bda3935eb3b51e6a143fac99ea08df.png) και η γενέτειρα γραμμή της
και η γενέτειρα γραμμή της Προφανώς είναι μια επιφάνεια, αλλά δεν είναι κανονική επιφάνεια -αφού το
 μηδενίζεται για κάποιες τιμές- και, επομένως, δεν μπορούμε να χρησιμοποιήσουμε την θεωρία που χρησιμοποίησε παραπάνω ο Σταύρος για να εξάγει το αποτέλεσμα.
μηδενίζεται για κάποιες τιμές- και, επομένως, δεν μπορούμε να χρησιμοποιήσουμε την θεωρία που χρησιμοποίησε παραπάνω ο Σταύρος για να εξάγει το αποτέλεσμα.
Αντρέα καλησπέρα....Ανδρέας Πούλος έγραψε: ↑Δευ Απρ 27, 2020 11:42 amΔεν έχω να συνεισφέρω κάτι στον εκπληκτικό αυτό διάλογο (εξάλλου δεν μπορώ) και στις λύσεις που δόθηκαν,
απλά θέλω να εκφράσω τον θαυμασμό μου για όσα έμαθα. Το Φόρουμ είναι ένα "Κέντρο μάθησης" ανοιχτό μέρα-νύχτα.
Το μόνο που μπορώ να κάνω είναι να αναρτήσω μια φωτογραφία κοχυλιού, η "εξέλιξη" του οποίου σχετίζεται έμμεσα με το θέμα της συζήτησης.
Σας ευχαριστώ πολύ.
Γρηγόρη γειά.grigkost έγραψε: ↑Κυρ Απρ 26, 2020 2:30 amΑυτό που είχα κατά νου είναι η πολύ γενικότερη περίπτωση που παρουσίασε ο Σταύρος στην αμέσως προηγούμενη δημοσίευση. Να σημειωθεί ότι πρόκειται για σημαντική γενίκευση αφού η διευθετούσαMihalis_Lambrou έγραψε: ↑Κυρ Απρ 19, 2020 10:49 pm...να συμπληρώσω ότι ζητείται το εμβαδόνμε απλό τρόπο, χωρίς να κάνουμε ολοκλήρωση. Ίσως αυτό έχει κατά νου ο Γρηγόρης...
μπορεί να είναι οποιαδήποτε κανονική καμπύλη για την οποία πρέπει να ισχύει
, όπου
η καμπυλότητα της
αν έχουμε μια φυσική παραμετρικοποίησή της.
Βέβαια στην περίπτωση που η διευθετούσα είναι έλικα, ο υπολογισμός του εμβαδού της σωληνοειδούς επιφάνειας χωρίς ολοκλήρωση έχει το δικό της ενδιαφέρον. Όπως και η αναλυτική προσέγγιση της εύρεσης της παραμετρικής παράστασης που έδωσε ο Κώστας.
 δεν μας εξασφαλίζει ότι οι κύκλοι δεν τέμνονται.
δεν μας εξασφαλίζει ότι οι κύκλοι δεν τέμνονται.![a:[0,l]\rightarrow \mathbb{R}^{3} a:[0,l]\rightarrow \mathbb{R}^{3}](/forum/ext/geomar/texintegr/latexrender/pictures/58978a50ea7d87c6a4fb035a6e91ec46.png)

Κώστα γειά.KDORTSI έγραψε: ↑Κυρ Απρ 26, 2020 8:46 amΚαλημέρα από Γρεβενά ...ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Απρ 25, 2020 11:15 pmΤο πρόβλημα είναι αν υπάρχει τέτοια επιφάνεια.grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
helicoid_surf.png
Δηλαδή οι κύκλοι να μην τέμνονται.(1)
Είναι σαφές ότι αν τοείναι ''μεγάλο'' υπάρχει πρόβλημα.
Θα φανεί και από την απόδειξη που θα κάνω παρακάτω.
Νομίζω ότι μπορεί να αποδειχθεί η ύπαρξη της επιφάνειας για''μικρό''
αλλά θα έχει πολύ φασαρία.
Η καμπύλη που είναι οδηγός της επιφάνειας μπορεί να είναι οποιαδήποτε .(2)
Τότε το πόσο μεγάλο μπορούμε να πάρουμε τοέχει σχέση με την καμπυλότητα
της καμπύλης.
........................................................
Για την παρατήρηση (1) :
Δηλαδή θα αποκλείαμε(;) από την έννοια του "σωληνοειδούς" και την περίπτωση που δείχνει το σχήμα:
Σωληνοειδές 3.png
Στο σχήμα αυτό η γωνίακινήθηκε στο διάστημα
και η γενέτειρα γραμμή της
επιφάνειας αυτής είναι κύκλος με ακτίνα τέτοια ώστε η παραγόμενη επιφάνεια δημιουργεί
"αλληλοτομές" που τις βλέπουμε στο σχήμα αυτό.( Αυτό που λέει η φράση (1), αν και ο κύκλος
που "γεννάει" το σωληνοειδές αυτό είναι ένας και δεν τέμνει ποτέ τον εαυτό του. Ίσως βέβαια η
έκφραση να θέλει να πει ότι τέμνονται τα ίχνη των κύκλων αυτών...)
Ασφαλώς και είναι μια ενδιαφέρουσα περίπτωση του γενικευμένου σωληνοειδούς που αξίζει μελέτη.
Εξάλλου τέτοιες επιφάνειες με ενδιαφέρουσες τοπολογικές ιδιότητες έχουν μελετηθεί,
όπως "η φιάλη του Klein" ή ακόμα "η επιφάνεια του Boy" η οποία φαίνεται στο ακόλουθο σχήμα:
Επιφάνεια του Boy 1.png
Για την παρατήρηση (2):
Προφανώς. Αρκεί οι καμπύλες αυτές να είναι κανονικές.
Κι ακόμα:
Αντί του κύκλου αυτού που παράγει τα σωληνοειδή αυτά, μπορούμε να θεωρήσουμε τρίγωνα, τετράγωνα,
πολύγωνα(κυρτά ή μη κυρτά), ακόμα και ελλείψεις, καρδιοειδείς καμπύλες κλπ. Έτσι θα μπορούσαμε
να απολαύσουμε το μεγαλείο της φύσης! της φύσης που τα μαθηματικά προσπαθούν να ερμηνεύσουν!
Κώστας Δόρτσιος
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Απρ 28, 2020 1:40 pmΣταύρε γειά σου...KDORTSI έγραψε: ↑Κυρ Απρ 26, 2020 8:46 amΚώστα γειά.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Απρ 25, 2020 11:15 pm...................................grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
helicoid_surf.png
Κώστας Δόρτσιος
Αυτό που υπάρχει στο 3 έχω την εντύπωση ότι δεν είναι επιφάνεια.
Εψαξα τους ορισμούς της επιφάνειας.
Με κανέναν από αυτούς που είδα δεν είναι.
Αν έχεις υπ οψιν σου κάποιον γράφτον.
Το σχήμα 3 που ανάρτησα, θεωρώντας ακτίνα μεγάλη ώστε να προκύπτουν "τομές" κατά την εξέλιξή της,
πιστεύω ότι είναι μια επιφάνεια παραμετρικής μορφής η οποία βέβαια σχεδιάστηκε από τη σχέση (6) της
δεύτερης ανάρτησης που έβαλα.
Δεν είναι όμως κανονική, γιατί στα σημεία εκείνα των "τομών" δεν ορίζεται η κάθετος, όπως αναφέρει
και ο Γρηγόρης σε ένα από τα μηνύματά του.
Έτσι η επιφάνεια αυτή ανήκει στην κατηγορία εκείνη που ορίζονται με παραμετρικές εξισώσεις.
https://lescoursdemathsdepjh.monsite-or ... 213bff.pdf
Για να φανεί ίσως καλύτερα αυτό παραθέτω μια εικόνα:
Ίσως αυτό φανεί καλύτερα, όταν θα παραθέσω( ίσως αύριο) και το τελικό μου μήνυμα, όπου υπολογίζω το εμβαδόν
του αρχικού σωληνοειδούς όπου το αποτέλεσμά μου συμφωνεί με τη δικιά σου άποψη όταν μελετά το θέμα αυτό
γενικότερα.
Κώστας Δόρτσιος
Καλησπέρα...grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
 .
.







 τότε
τότε  απορρίπτεται.
απορρίπτεται.  τότε
τότε 


ενω είναι


Η δικαιολόγηση μπορεί να γίνει και ως εξής:
 το βρίσκουμε.
το βρίσκουμε.Γρηγόρη και Σταύρο καλησπέρα και καλό μήνα...grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.

 είναι το μέσο του τμήματος
είναι το μέσο του τμήματος  με
με  τα άκρα της αρχικής έλικας.
τα άκρα της αρχικής έλικας.  είναι η γωνία που σχηματίζει η
είναι η γωνία που σχηματίζει η  με το επίπεδο του κύκλου αυτού.
με το επίπεδο του κύκλου αυτού.  , την αρχική έλικα, ή καλύτερα, σχεδιάζοντας
, την αρχική έλικα, ή καλύτερα, σχεδιάζοντας 
Γρηγόρη καλησπέρα...grigkost έγραψε: ↑Κυρ Απρ 19, 2020 9:06 amΘεωρούμε την σωληνοειδή επιφάνειαμε διευθετούσα την έλικα
![{\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,, {\bf{c}}(t)=(\alpha\cos{t},\alpha\sin{t},\beta\, t )\,, \; t\in [0,2\pi],\; \alpha>0,\; \beta>0\,,](/forum/ext/geomar/texintegr/latexrender/pictures/8ad6e89471d8efb9872b1247a5bce1c5.png)
για την οποία, σε κάθε σημείοτης
, η τομή της
με το κάθετο στην
επίπεδο είναι κύκλος με κέντρο το
και ακτίνα
.
Να βρεθεί μια παραμετρική παράσταση της επιφάνειαςκαι να υπολογισθεί το εμβαδόν της
.
 και
και με μήκος ίσο με το μήκος της έλικας
με μήκος ίσο με το μήκος της έλικας  .
. και κύκλο τον
και κύκλο τον  .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης