Να βρείτε όλες τις συναρτήσεις
 για τις οποίες ισχύει
για τις οποίες ισχύει 
για όλους τους πραγματικούς αριθμούς

ΘΕΜΑ 2
 φορτηγά είναι διαθέσιμα για τη μεταφορά
φορτηγά είναι διαθέσιμα για τη μεταφορά  κιλών καρπούζια. Κάθε καρπούζι ζυγίζει το πολύ
κιλών καρπούζια. Κάθε καρπούζι ζυγίζει το πολύ  κιλά, ενώ κάθε φορτηγό μπορεί να μεταφέρει μέχρι
κιλά, ενώ κάθε φορτηγό μπορεί να μεταφέρει μέχρι  κιλά καρπούζια σε κάθε δρομολόγιο. Αν κάθε φορτηγό μπορεί να κάνει το πολύ ένα δρομολόγιο, να αποδείξετε ότι είναι δυνατόν να μεταφερθούν όλα τα καρπούζια!
κιλά καρπούζια σε κάθε δρομολόγιο. Αν κάθε φορτηγό μπορεί να κάνει το πολύ ένα δρομολόγιο, να αποδείξετε ότι είναι δυνατόν να μεταφερθούν όλα τα καρπούζια! ΘΕΜΑ 3
Να βρείτε όλα τα ζεύγη θετικών ακεραίων
 για τα οποία ισχύει
για τα οποία ισχύει 
ΘΕΜΑ 4
Θεωρούμε τρίγωνο
 με
με  Ο εγγεγραμμένος κύκλος
Ο εγγεγραμμένος κύκλος  του τριγώνου
του τριγώνου  εφάπτεται στις πλευρές
εφάπτεται στις πλευρές  στα σημεία
στα σημεία 
Η ευθεία
 τέμνει τον κύκλο
τέμνει τον κύκλο  για δεύτερη φορά στο
για δεύτερη φορά στο  Έστω
Έστω  το σημείο τομής της
το σημείο τομής της  με την κάθετη στην
με την κάθετη στην  στο
στο 
Έστω, τέλος,
 τα σημεία τομής της
τα σημεία τομής της  με την
με την  και την
και την  αντίστοιχα.
αντίστοιχα.Δείξτε ότι το
 είναι το μέσο του τμήματος
είναι το μέσο του τμήματος 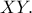

 .
. λαμβάνουμε πως το
λαμβάνουμε πως το  .
. .
. στην
στην  η δοσμένη.
η δοσμένη.  δίνει
δίνει  , άρα αν
, άρα αν  προκύπτει ότι
προκύπτει ότι  για κάθε
για κάθε  , άτοπο.
, άτοπο. . Άρα, η
. Άρα, η  δίνει
δίνει  .
. στην προηγούμενη και έχω
στην προηγούμενη και έχω  , άρα
, άρα  .
.
 Αν
Αν 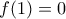 , τότε η
, τότε η  δίνει
δίνει  , οπότε
, οπότε  , δηλαδή
, δηλαδή 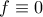 , που ικανοποιεί την συνθήκη.
, που ικανοποιεί την συνθήκη. , τότε η (*) με
, τότε η (*) με  για κάθε
για κάθε  . Επίσης, με
. Επίσης, με  η (*) δίνει
η (*) δίνει 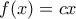 για κάθε
για κάθε  (με
(με  ).
).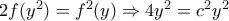 , οπότε
, οπότε  ή
ή 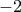 . Επομένως, έχω τις τρεις λύσεις:
. Επομένως, έχω τις τρεις λύσεις: , και η
, και η  και
και  .
. . Τότε
. Τότε  δίνει πως
δίνει πως  . H δεύτερη απορρίπτεται αφού στο
. H δεύτερη απορρίπτεται αφού στο  (άπειρες) τιμές. Έτσι,
(άπειρες) τιμές. Έτσι, 
 . Άρα
. Άρα  για
για  για
για  και
και  . Άρα
. Άρα  για
για  για
για  δίνουν τις
δίνουν τις  λύσεις μας.
λύσεις μας.
 οπότε αλλάζουν λίγο οι λύσεις...
οπότε αλλάζουν λίγο οι λύσεις...  έχω ότι
έχω ότι  . Έστω
. Έστω  , οπότε γράφω
, οπότε γράφω  .
. , οπότε διακρίνω 2 περιπτώσεις.
, οπότε διακρίνω 2 περιπτώσεις. . Τότε, έχω αναγκαστικά δύο περιπτώσεις:
. Τότε, έχω αναγκαστικά δύο περιπτώσεις: και
και  με
με  θετικούς ακεραίους, ή
θετικούς ακεραίους, ή και
και  με
με  στην
στην  , οπότε
, οπότε  και
και  . Τελικά
. Τελικά  .
. , άτοπο.
, άτοπο. . Τότε, αν πάρω
. Τότε, αν πάρω  , πρέπει
, πρέπει  , άρα
, άρα  . Άρα προκύπτει
. Άρα προκύπτει  με
με  . Οπότε θα προκύψουν πάλι 2 περιπτώσεις:
. Οπότε θα προκύψουν πάλι 2 περιπτώσεις: και
και  , ή
, ή και
και  .
. προκύπτει
προκύπτει  , δηλαδή
, δηλαδή  , άτοπο για
, άτοπο για  , οπότε
, οπότε  ή
ή  και
και  .
. , οπότε
, οπότε  , άρα
, άρα  . Οι δοκιμές δεν δίνουν κάποια λύση.
. Οι δοκιμές δεν δίνουν κάποια λύση. .
. . Συγκεκριμένα,
. Συγκεκριμένα, ως το σημείο τομής του κύκλου
ως το σημείο τομής του κύκλου  με την
με την  .
. ως το σημείο τομής του κύκλου
ως το σημείο τομής του κύκλου  με την
με την  είναι συνευθειακά, ότι ισχύει
είναι συνευθειακά, ότι ισχύει  , και ότι η
, και ότι η  περνάει από το
περνάει από το  .
. , άρα
, άρα  , και όμοια
, και όμοια  , οπότε
, οπότε  , και όμοια
, και όμοια  , άρα
, άρα  .
. . Είναι,
. Είναι,  , Και επίσης
, Και επίσης  , άρα τα
, άρα τα  και
και  είναι όμοια. Οπότε,
είναι όμοια. Οπότε, , οπότε και τα
, οπότε και τα  και
και  είναι όμοια. Επομένως
είναι όμοια. Επομένως  .
. .
. .
. είναι εγγράψιμο, όπως και τα
είναι εγγράψιμο, όπως και τα  και
και  (το τελευταίο διότι
(το τελευταίο διότι  ).
). , συντρέχουν στο ριζικό κέντρο των τριών κύκλων. Οπότε, όντως η
, συντρέχουν στο ριζικό κέντρο των τριών κύκλων. Οπότε, όντως η  .
. , και ανήκουν και στην
, και ανήκουν και στην  αντίστοιχα, όπως και αυτά της εκφώνησης. Άρα τα σημεία αυτά ταυτίζονται, οπότε έχω ότι
αντίστοιχα, όπως και αυτά της εκφώνησης. Άρα τα σημεία αυτά ταυτίζονται, οπότε έχω ότι  μας τα χαλάει. (δεν χωράει πουθενά ). Τότε αν
μας τα χαλάει. (δεν χωράει πουθενά ). Τότε αν  , ...,
, ...,  τα αθροίσματα των κιλών στο κάθε φορτηγό πρέπει
τα αθροίσματα των κιλών στο κάθε φορτηγό πρέπει  ,...,
,...,  . Προσθέτοντας,
. Προσθέτοντας,  . Το δεξί μέλος όμως είναι μικρότερο ή ίσο του
. Το δεξί μέλος όμως είναι μικρότερο ή ίσο του 

 . Έχουμε δηλαδή, ότι όλα τα καρπούζια που έχουν μπει σε φορτηγό συν το
. Έχουμε δηλαδή, ότι όλα τα καρπούζια που έχουν μπει σε φορτηγό συν το  . Δηλαδή,
. Δηλαδή, 


 . Τότε όμως μπορούμε να αφαιρέσουμε τα καρπούζια που έχουμε βάλει στα φορτηγά και μαζί με το Μ να τα χωρίσουμε σε
. Τότε όμως μπορούμε να αφαιρέσουμε τα καρπούζια που έχουμε βάλει στα φορτηγά και μαζί με το Μ να τα χωρίσουμε σε  .
. .
. κιλά.(περίσσευμα πάνω από
κιλά.(περίσσευμα πάνω από  κιλά).
κιλά). φορτηγά έχουν "γεμίσει" με καρπούζια με μάζες πάνω από
φορτηγά έχουν "γεμίσει" με καρπούζια με μάζες πάνω από  (χωράνε τουλάχιστον
(χωράνε τουλάχιστον  επίσης:Αν όχι,θα χωρούσε κι άλλο "μικρό" καρπούζι.
επίσης:Αν όχι,θα χωρούσε κι άλλο "μικρό" καρπούζι. άρτιο θέτω
άρτιο θέτω  οπότε παίρνω
οπότε παίρνω  και αφού
και αφού  έχω δύο περιπτώσεις
έχω δύο περιπτώσεις  και
και  η πρώτη δίνει εύκολα
η πρώτη δίνει εύκολα  και η δεύτερη άτοπο για
και η δεύτερη άτοπο για  με
με  δηλαδή
δηλαδή  αδύνατο. Άρα εδώ
αδύνατο. Άρα εδώ 
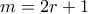 και
και  οπότε
οπότε  , (
, ( )
) έχει θεμελιώδη την
έχει θεμελιώδη την  οπότε αφού
οπότε αφού  θεμελιώδης της
θεμελιώδης της  βρίσκουμε
βρίσκουμε  από τις γνωστές σχέσεις. Επίσης παίρνουμε την αναδρομική
από τις γνωστές σχέσεις. Επίσης παίρνουμε την αναδρομική 
 άρα για να είναι
άρα για να είναι  και έτσι
και έτσι