Έστω
![[x] [x]](/forum/ext/geomar/texintegr/latexrender/pictures/3e5314e9fd31509fdeb83faa0f729ba2.png) το ακέραιο μέρος του
το ακέραιο μέρος του  και
και ![\{x\} = x − [x] \{x\} = x − [x]](/forum/ext/geomar/texintegr/latexrender/pictures/7f61dbfa825b8a75dbc45452c6ebab53.png) το δεκαδικό του μέρος. Να λύσετε στο
το δεκαδικό του μέρος. Να λύσετε στο  την εξίσωση
την εξίσωση ![\displaystyle{3\{x\} = x[x] + 1.} \displaystyle{3\{x\} = x[x] + 1.}](/forum/ext/geomar/texintegr/latexrender/pictures/f8979dcba58a09335b65d27de18f4cee.png)
ΘΕΜΑ 2
Θεωρούμε οξυγώνιο τρίγωνο
 το ύψος του
το ύψος του  και το ορθόκεντρό του
και το ορθόκεντρό του  Φέρουμε εφαπτομένη από το σημείο
Φέρουμε εφαπτομένη από το σημείο  στον κύκλο κέντρου
στον κύκλο κέντρου  και ακτίνας
και ακτίνας  και έστω
και έστω  το σημείο επαφής. Φέρουμε ακόμη εφαπτομένη από το
το σημείο επαφής. Φέρουμε ακόμη εφαπτομένη από το  στον κύκλο κέντρου
στον κύκλο κέντρου  και ακτίνας
και ακτίνας  και έστω
και έστω  το σημείο επαφής. Να δείξετε ότι η ευθεία
το σημείο επαφής. Να δείξετε ότι η ευθεία 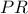 περνάει από δύο ίχνη υψών του τριγώνου
περνάει από δύο ίχνη υψών του τριγώνου 
ΘΕΜΑ 3
Οι θετικοί ακέραιοι
 και
και  είναι τέτοιοι ώστε
είναι τέτοιοι ώστε 
Να δείξετε ότι ο
 διαιρεί τον
διαιρεί τον  και ότι ο
και ότι ο  είναι της μορφής
είναι της μορφής  για κάποιον θετικό ακέραιο
για κάποιον θετικό ακέραιο 
ΘΕΜΑ 4
Σε μια ακολουθία θετικών ακεραίων, ονομάζουμε αντιστροφή ένας ζεύγος θέσεων για το οποίο ο όρος που βρίσκεται στα αριστερά είναι μεγαλύτερος από τον όρο στα δεξιά.
Για παράδειγμα, η ακολουθία
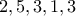 έχει ακριβώς πέντε αντιστροφές.
έχει ακριβώς πέντε αντιστροφές. Ποιος είναι ο μεγαλύτερος δυνατός αριθμός αντιστροφών που μπορεί να έχει μια ακολουθία θετικών ακεραίων με άθροισμα


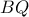 εφαπτόμενο τμήμα στον
εφαπτόμενο τμήμα στον  και
και  εφαπτόμενο τμήμα στον
εφαπτόμενο τμήμα στον  .Έστω
.Έστω  ύψη.Από το πρόβλημα
ύψη.Από το πρόβλημα  συνευθειακά και
συνευθειακά και  συνευθειακά.Όμως
συνευθειακά.Όμως  και
και  οπότε η
οπότε η  θα περνά από το
θα περνά από το  .Όμοια και η
.Όμοια και η  θα περνά από το
θα περνά από το  και το ζητούμενο έπεται.
και το ζητούμενο έπεται.![[x] =k [x] =k](/forum/ext/geomar/texintegr/latexrender/pictures/cc27c1439f2520de8b15a91cce3eadce.png) και
και 
 (1)
(1)
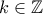
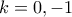 .
.
 και την μέγιστη δύναμή του που διαιρεί καθέναν από αυτούς...
και την μέγιστη δύναμή του που διαιρεί καθέναν από αυτούς...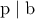 είναι
είναι  .Είναι
.Είναι 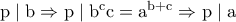 .Έστω ότι
.Έστω ότι  , γράφουμε
, γράφουμε  .
.  .
. αφού
αφού  .Από τα παραπάνω
.Από τα παραπάνω  .
. άτοπο!
άτοπο! ένας πρώτος διαιρέτης του
ένας πρώτος διαιρέτης του 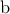 που όπως δείξαμε θα είναι και των
που όπως δείξαμε θα είναι και των  .
. με
με 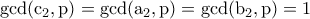
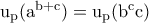 από όπου
από όπου  .
. και
και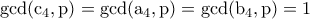 .
. αφού
αφού  .
. .Αν ήταν
.Αν ήταν  τότε
τότε  άτοπο.Άρα
άτοπο.Άρα 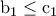 .
. έπεται ότι
έπεται ότι 
 πρώτος που διαιρεί τον
πρώτος που διαιρεί τον  . Για συντομία
. Για συντομία 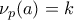 ,
,  και
και  .
. και
και 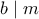 .
. 
 , τότε από την
, τότε από την 

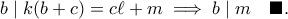
 πρέπει να παρθεί ξεχωριστά, αλλά δεν αλλάζει κάτι.
πρέπει να παρθεί ξεχωριστά, αλλά δεν αλλάζει κάτι. ο μέγιστος αριθμός αντιστροφών είναι ο
ο μέγιστος αριθμός αντιστροφών είναι ο  .Έτσι για
.Έτσι για  το αποτέλεσμα είναι
το αποτέλεσμα είναι  και μπορεί να επιτευχθεί ως εξής :
και μπορεί να επιτευχθεί ως εξής :  .
. ακολουθία θετικών ακεραίων με
ακολουθία θετικών ακεραίων με  ,
, με
με  θεωρώ την ακολουθία
θεωρώ την ακολουθία  η οποία έχει μία επιπλέον αντιστροφή από την αρχική.
η οποία έχει μία επιπλέον αντιστροφή από την αρχική.
 τέτοιος ώστε να είναι ο δεξιότερος όρος της ακολουθίας που να είναι
τέτοιος ώστε να είναι ο δεξιότερος όρος της ακολουθίας που να είναι  (αν υπάρχει) οπότε
(αν υπάρχει) οπότε  .
. όπου το
όπου το  ώστε
ώστε  αλλά
αλλά  (ενδέχεται
(ενδέχεται  )
)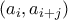 με
με  και αυτό στην περίπτωση που
και αυτό στην περίπτωση που  .
. με
με  και σαφώς
και σαφώς  ! .
! . -άρια(και επίσης να φθίνει)
-άρια(και επίσης να φθίνει) με
με 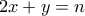 και θέλω να μεγιστοποιήσω το
και θέλω να μεγιστοποιήσω το  που είναι ο αριθμός των αντιστροφών της.
που είναι ο αριθμός των αντιστροφών της.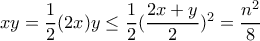
 πρέπει να είναι εφικτό αλλά δεν το κοίταξα.
πρέπει να είναι εφικτό αλλά δεν το κοίταξα. έχει λύση στους φυσικούς.
έχει λύση στους φυσικούς. παίρνω
παίρνω 
 είναι πάντα τέλειο τετράγωνο, αυτό το βλέπουμε θέτοντας
είναι πάντα τέλειο τετράγωνο, αυτό το βλέπουμε θέτοντας  οπότε βλέπουμε πως
οπότε βλέπουμε πως  και ελέγχουμε
και ελέγχουμε 