Καλησπέρα,ευχαριστώ για το ενδιαφέρον και συγγνώμη για την καθυστέρηση.
Ομολογώ πως δεν έχω τσεκάρει πλήρως τις πράξεις του κ. Γιώργου.
Όπως είδα πάντως την Αναλυτική μέθοδο είχα σκεφτεί να εργαστώ με οικογένειες Κωνικών και βρήκα μια αυτοσχέδια λύση παρόμοια όμως στη φιλοσοφία εκείνης του κ. Αλέξανδρου-οπότε δεν την ανεβάζω.
Αυτοσχεδίασα ξανά μπαίνοντας σε πιο γνώριμα μονοπάτια και κάτι βρήκα-πιο Γεωμετρικό με ένα επιπλέον ωραίο Αλγεβρικό επιχείρημα.
Οπότε πρώτα το αλγεβρικό επιχείρημα:
1)Σε κάθε -μη εκφυλισμένη-οικογένεια κωνικών,είτε κάθε διεύθυνση (αξόνων) εμφανίζεται πεπερασμένες φορές,είτε υπάρχει μόνο ένα ζεύγος διευθύνσεων (κάθετων αξόνων-με εξαίρεση την παραβολή που έχει 1 άξονα).
Απόδειξη: Έστω

οι εξισώσεις 2 εκ των κωνικών της οικογένειας.
Κάθε κωνική της οικογένειας γράφεται ως
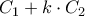
όπου

παράμετρος και με μοναδικό μάλιστα τρόπο.
Αν υποθέσουμε πως κάποια διεύθυνση αξόνων εμφανίζεται άπειρες φορές,τότε από εδώ
https://math.stackexchange.com/question ... ic-section προκύπτει μια ρητή παράσταση ως προς

που μηδενίζει για άπειρες τιμές του

.Επομένως η ρητή παράσταση είναι ταυτοτικά

κλπ .
Πάμε πλέον στο Γεωμετρικό κομμάτι.
Καταρχάς παρατηρούμε ότι :
2)Δεδομένων τεσσάρων σημείων τα οποία ανά

είναι μη συνευθειακά,υπάρχουν άπειρες Υπερβολές που ανήκουν στην οικογένεια που ορίζεται από αυτά τα σημεία.
Πράγματι αρκεί να επιλέξουμε για πέμπτο σημείο σημεία στην ευθεία στο άπειρο:το πολύ

από αυτά δίνουν παραβολή (τα σταθερά σημεία της ευθείας στο άπειρο υπό την ενέλιξη που δημιουργεί η οικογένεια) και όλα τα υπόλοιπα δίνουν Υπερβολή όπως θέλαμε.
Γιατί όμως επιλέγουμε να "δούμε" τις Υπερβολές;
Η απάντηση είναι :Ασύμπτωτοι.
Δείχνουμε το Γεωμετρικό κομμάτι.
3)"Δεδομένου εγγράψιμου τετραπλεύρου

να δειχθεί ότι οι περιγεγγραμμένες Υπερβολές του έχουν όλες την ίδια διεύθυνση αξόνων."
Οι άξονες της Υπερβολής δεν είναι τίποτε άλλο παρά οι διχοτόμοι της γωνίας που σχηματίζουν οι Ασύμπτωτοι της.
Θεωρώντας τον ισογώνιο μετασχηματισμό ως προς το

και λόγω του κοινού σημείου στον περίκυκλο,οι Υπερβολές (έστω

δύο από αυτές) μετασχηματίζονται σε παράλληλες ευθείες (έστω

).
Ας είναι

και
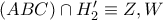
.
Από γνωστή θεωρία,οι Ασύμπτωτες της

έχουν διεύθυνσεις κάθετες στις ευθείες

των

και εκείνες της

σε εκείνες των

.
Οι τέσσερις ευθείες

,

κατά σειρά (που έχουν ίδια διεύθυνση με τις αντίστοιχες

) περνούν από κοινό σημείο-το Ορθόκεντρο του

.
Επιπλέον είναι απλό ότι οι

έχουν κοινές διχοτόμους-λόγω των ίσων τόξων

.
Συνεπώςτο ίδιο θα ισχύει και για τις Ασυμπτώτους.
Τέλος,το ζητούμενο έπεται από

..
*Ίσως να χει ξεφύγει τίποτα γιατί γράφω και από κινητό
Edit:Ουσιαστικά δείχτηκε η πρόταση του κ.Αλέξανδρου που είναι η αντίστροφη της αρχικής.
Για το ευθύ μπορούμε να πάμε με άτοπο :Υποθέτουμε ότι οι δύο κωνικές τέμνονται στα

που είναι μη ομοκυκλικά,και επανατέμνουν τον

στα

.
Κάθε μία από αυτές δημιουργεί μαζί με τον κύκλο μια οικογένεια,ενώ οι

οικογένειες έχουν ίδιες-κάθετες διευθύνσεις αξόνων (αντίστροφο-δείχτηκε παραπάνω).
Μπορούμε για ευκολία να θεωρήσουμε τις

οι οποίες έχουν άξονες τις διχοτόμος των γωνιών που προκύπτουν.Μπορούμε να δούμε πως για να έχουν οι διχοτόμοι ίδια διεύθυνση πρέπει απαραίτητα

που είναι άτοπο από υπόθεση.
Edit2:Άλλαξα ένα επιχείρημα
 σημεία στα οποία τέμνονται
σημεία στα οποία τέμνονται  ελλείψεις με κάθετους μεταξύ τους άξονες είναι ομοκυκλικά.
ελλείψεις με κάθετους μεταξύ τους άξονες είναι ομοκυκλικά. κύκλοι και μια Κωνική που δεν είναι κύκλος,που τέμνονται σε
κύκλοι και μια Κωνική που δεν είναι κύκλος,που τέμνονται σε  κοινά για όλους σημεία.
κοινά για όλους σημεία. σημεία τομής που περισσεύουν (κύκλου/κωνικής και άλλου κύκλου/κωνικής) ορίζουν παράλληλες μεταξύ τους ευθείες.
σημεία τομής που περισσεύουν (κύκλου/κωνικής και άλλου κύκλου/κωνικής) ορίζουν παράλληλες μεταξύ τους ευθείες.
 ,
,  :
: τα σημεία τομής, οπότε ισχύει η
τα σημεία τομής, οπότε ισχύει η  .
. διερχόμενου δια των
διερχόμενου δια των 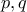 : παρατηρούμε ότι οφείλει να ισχύει η
: παρατηρούμε ότι οφείλει να ισχύει η
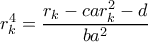 και της
και της  , ανάγεται στην
, ανάγεται στην
 , αν
, αν  και
και  . Επειδή όλα τα βήματα είναι αντιστρεπτά, συμπεραίνουμε ότι το σημείο
. Επειδή όλα τα βήματα είναι αντιστρεπτά, συμπεραίνουμε ότι το σημείο  είναι κέντρο κύκλου επί του οποίου κείνται τα τέσσερα σημεία τομής των δύο παραβολών.
είναι κέντρο κύκλου επί του οποίου κείνται τα τέσσερα σημεία τομής των δύο παραβολών. έχουν 4 κοινά σημεία τότε αυτά κείνται επί κύκλου κέντρου
έχουν 4 κοινά σημεία τότε αυτά κείνται επί κύκλου κέντρου  .
. έχουν 4 κοινά σημεία τότε αυτά κείνται επί κύκλου κέντρου
έχουν 4 κοινά σημεία τότε αυτά κείνται επί κύκλου κέντρου  .
. και
και  ας πούμε (που είναι τυπικά και το αρχικό ερώτημα), λίγο πιο δύσκολα αλλά στο ίδιο πνεύμα:
ας πούμε (που είναι τυπικά και το αρχικό ερώτημα), λίγο πιο δύσκολα αλλά στο ίδιο πνεύμα: , όπου
, όπου 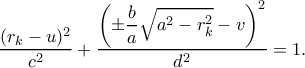

 , επιτρέποντας την παραγοντοποίηση
, επιτρέποντας την παραγοντοποίηση  στην 'εξίσωση κέντρου'
στην 'εξίσωση κέντρου' 

 ,
, 
 ,
,  ... που επαληθεύει τους προηγούμενους:
... που επαληθεύει τους προηγούμενους: ,
, 
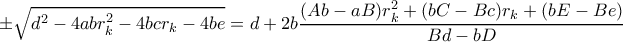
-\left[\dfrac{d(Bc-bC)}{b(Bd-bD)}+\dfrac{2(Bc-bC)q}{Bd-bD}-\dfrac{c}{b}-2p\right]=0 \left[1-\dfrac{a}{b}+\dfrac{d(aB-Ab)}{b(Bd-bD)}+\dfrac{2(aB-Ab)q}{Bd-bD}\right](r_i+r_j)-\left[\dfrac{d(Bc-bC)}{b(Bd-bD)}+\dfrac{2(Bc-bC)q}{Bd-bD}-\dfrac{c}{b}-2p\right]=0](/forum/ext/geomar/texintegr/latexrender/pictures/7259e8f06dd5a084b5d124736ac133d6.png)
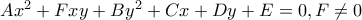 , αν δηλαδή οι δύο κωνικές δεν είναι ορθογώνιες (δεν τέμνονται κάθετα οι άξονες τους), τότε η εξίσωση κύκλου
, αν δηλαδή οι δύο κωνικές δεν είναι ορθογώνιες (δεν τέμνονται κάθετα οι άξονες τους), τότε η εξίσωση κύκλου 

 ,
,  μηδενίζονται οι συντελεστές των
μηδενίζονται οι συντελεστές των  ,
,  ίσο προς
ίσο προς  (περίπτωση
(περίπτωση  ) είτε
) είτε  ). (Στην πρώτη περίπτωση ο συντελεστής του
). (Στην πρώτη περίπτωση ο συντελεστής του  , οπότε η κωνική είναι κύκλος (και το πρόβλημα καθίσταται τετριμμένο).)
, οπότε η κωνική είναι κύκλος (και το πρόβλημα καθίσταται τετριμμένο).) και ορθογώνιες κωνικές -- ο υπολογισμός της ακτίνας του κύκλου των 4 σημείων:
και ορθογώνιες κωνικές -- ο υπολογισμός της ακτίνας του κύκλου των 4 σημείων:
 ):
): και με αντικατάσταση στην δεύτερη κωνική λαμβάνουμε
και με αντικατάσταση στην δεύτερη κωνική λαμβάνουμε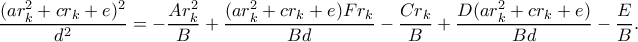
 , διότι τότε θα είχαμε δύο 'παράλληλες' παραβολές τεμνόμενες σε 4 σημεία!]
, διότι τότε θα είχαμε δύο 'παράλληλες' παραβολές τεμνόμενες σε 4 σημεία!]


 έχουμε και πάλι καταλήξει σε τριτοβάθμια με 4 ρίζες, άτοπο. Ισχύει λοιπόν αναγκαστικά η
έχουμε και πάλι καταλήξει σε τριτοβάθμια με 4 ρίζες, άτοπο. Ισχύει λοιπόν αναγκαστικά η 
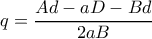 και
και  , επαληθεύοντας τους γενικούς τύπους κέντρου που έχω δώσει, ενώ για την ακτίνα δίνει
, επαληθεύοντας τους γενικούς τύπους κέντρου που έχω δώσει, ενώ για την ακτίνα δίνει
 .
. . Αν ο γραμμικός συνδιασμός των παραπάνω δυο κωνικών είναι της μορφής
. Αν ο γραμμικός συνδιασμός των παραπάνω δυο κωνικών είναι της μορφής  (δηλαδή κύκλος), τότε
(δηλαδή κύκλος), τότε  , άρα οι άξονες των κωνικών είναι κάθετοι.
, άρα οι άξονες των κωνικών είναι κάθετοι.  . Θέτουμε
. Θέτουμε  (η περίπτωση
(η περίπτωση  αντιστοιχεί σε κύκλους). Τότε
αντιστοιχεί σε κύκλους). Τότε  . Μένει να παρατηρήσουμε ότι, αν
. Μένει να παρατηρήσουμε ότι, αν  , τότε οι υπό εξέταση κωνικές έχουν το πολύ δυο κοινά σημεία, καθώς μεταξύ των γραμμικών συνδιασμών τους υπάρχουν γραμμικές εξισώσεις.
, τότε οι υπό εξέταση κωνικές έχουν το πολύ δυο κοινά σημεία, καθώς μεταξύ των γραμμικών συνδιασμών τους υπάρχουν γραμμικές εξισώσεις. οι εξισώσεις 2 εκ των κωνικών της οικογένειας.
οι εξισώσεις 2 εκ των κωνικών της οικογένειας.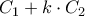 όπου
όπου  παράμετρος και με μοναδικό μάλιστα τρόπο.
παράμετρος και με μοναδικό μάλιστα τρόπο. κλπ .
κλπ . είναι μη συνευθειακά,υπάρχουν άπειρες Υπερβολές που ανήκουν στην οικογένεια που ορίζεται από αυτά τα σημεία.
είναι μη συνευθειακά,υπάρχουν άπειρες Υπερβολές που ανήκουν στην οικογένεια που ορίζεται από αυτά τα σημεία. να δειχθεί ότι οι περιγεγγραμμένες Υπερβολές του έχουν όλες την ίδια διεύθυνση αξόνων."
να δειχθεί ότι οι περιγεγγραμμένες Υπερβολές του έχουν όλες την ίδια διεύθυνση αξόνων." και λόγω του κοινού σημείου στον περίκυκλο,οι Υπερβολές (έστω
και λόγω του κοινού σημείου στον περίκυκλο,οι Υπερβολές (έστω  δύο από αυτές) μετασχηματίζονται σε παράλληλες ευθείες (έστω
δύο από αυτές) μετασχηματίζονται σε παράλληλες ευθείες (έστω  ).
). και
και 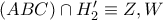 .
. έχουν διεύθυνσεις κάθετες στις ευθείες
έχουν διεύθυνσεις κάθετες στις ευθείες  των
των  και εκείνες της
και εκείνες της  σε εκείνες των
σε εκείνες των  .
. ,
, κατά σειρά (που έχουν ίδια διεύθυνση με τις αντίστοιχες
κατά σειρά (που έχουν ίδια διεύθυνση με τις αντίστοιχες  έχουν κοινές διχοτόμους-λόγω των ίσων τόξων
έχουν κοινές διχοτόμους-λόγω των ίσων τόξων  .
. ..
.. που είναι μη ομοκυκλικά,και επανατέμνουν τον
που είναι μη ομοκυκλικά,και επανατέμνουν τον  στα
στα  οι οποίες έχουν άξονες τις διχοτόμος των γωνιών που προκύπτουν.Μπορούμε να δούμε πως για να έχουν οι διχοτόμοι ίδια διεύθυνση πρέπει απαραίτητα
οι οποίες έχουν άξονες τις διχοτόμος των γωνιών που προκύπτουν.Μπορούμε να δούμε πως για να έχουν οι διχοτόμοι ίδια διεύθυνση πρέπει απαραίτητα  που είναι άτοπο από υπόθεση.
που είναι άτοπο από υπόθεση. .
. μέσα των ευθυγράμμων τμημάτων που ορίζουν αν ενώσουμε ζεύγη αυτών των σημείων και από τα
μέσα των ευθυγράμμων τμημάτων που ορίζουν αν ενώσουμε ζεύγη αυτών των σημείων και από τα  είναι το σημείο τομής των υψών του τριγώνου
είναι το σημείο τομής των υψών του τριγώνου  μια κωνική της κλάσης
μια κωνική της κλάσης  (δηλαδή την έχουμε περιστρέψει κατάλληλα ώστε οι άξονές τις να είναι παράλληλλοι με τους άξονες συντεταγμένων) και
(δηλαδή την έχουμε περιστρέψει κατάλληλα ώστε οι άξονές τις να είναι παράλληλλοι με τους άξονες συντεταγμένων) και  διαφορετικά μεταξύ τους σημεία αυτής της κωνικής τέτοια, ώστε η
διαφορετικά μεταξύ τους σημεία αυτής της κωνικής τέτοια, ώστε η 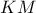 , ούτε την ευθεία
, ούτε την ευθεία 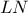 . Τα σημεία
. Τα σημεία  , που έχει άξονες τις διχοτόμους της
, που έχει άξονες τις διχοτόμους της  .Μπορούμε όμως να δούμε με απλό κυνήγι γωνιών πως αυτές οι διχοτόμοι έχουν την ιδιότητα που θέμε,οπότε λόγω παραλληλίας-καθετότητας το ίδιο θα ισχύει για όλους τους άξονες της οικογένειας..
.Μπορούμε όμως να δούμε με απλό κυνήγι γωνιών πως αυτές οι διχοτόμοι έχουν την ιδιότητα που θέμε,οπότε λόγω παραλληλίας-καθετότητας το ίδιο θα ισχύει για όλους τους άξονες της οικογένειας.. .
. } τα τέσσερα σημεία τομής της παραβολής
} τα τέσσερα σημεία τομής της παραβολής  . Για την ζητούμενη αντιπαραλληλία αρκεί προφανώς να δείξουμε ότι ισχύει η εξίσωση κλίσεων
. Για την ζητούμενη αντιπαραλληλία αρκεί προφανώς να δείξουμε ότι ισχύει η εξίσωση κλίσεων
 των
των  .
. και την κλίση
και την κλίση  προκύπτει άμεσα ότι αρκεί να δειχθεί η
προκύπτει άμεσα ότι αρκεί να δειχθεί η  . Αυτό όντως συμβαίνει επειδή οι
. Αυτό όντως συμβαίνει επειδή οι  είναι ρίζες της εξίσωσης τομής
είναι ρίζες της εξίσωσης τομής  , μιας τεταρτοβάθμιας χωρίς τριτοβάθμιο όρο.
, μιας τεταρτοβάθμιας χωρίς τριτοβάθμιο όρο.  και του κύκλου
και του κύκλου  στην
στην 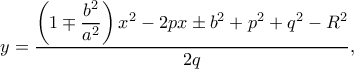
![4q^2\left(\pm b^2\mp \dfrac{b^2}{a^2}x^2\right)=\left[\left(1\mp \dfrac{b^2}{a^2}\right)x^2-2px\pm b^2+p^2+q^2-R^2\right]^2 4q^2\left(\pm b^2\mp \dfrac{b^2}{a^2}x^2\right)=\left[\left(1\mp \dfrac{b^2}{a^2}\right)x^2-2px\pm b^2+p^2+q^2-R^2\right]^2](/forum/ext/geomar/texintegr/latexrender/pictures/a25625afd06f33cf190fb0df70e1d6bf.png)

