 , τεταρτοκυκλίου
, τεταρτοκυκλίου  , θεωρούμε σημείο
, θεωρούμε σημείο  , με :
, με : 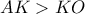 . Σχεδιάζω
. Σχεδιάζωκαι το τεταρτοκύκλιο
 , το οποίο τέμνει το αρχικό στο σημείο
, το οποίο τέμνει το αρχικό στο σημείο  . Ο κύκλος
. Ο κύκλος  τέμνει
τέμνειτο μικρό τεταρτοκύκλιο στο
 . Αν τα
. Αν τα  είναι συνευθειακά , υπολογίστε τον λόγο :
είναι συνευθειακά , υπολογίστε τον λόγο :  .
.Αν το τμήμα
 , τέμνει το μεγάλο τεταρτοκύκλιο στο
, τέμνει το μεγάλο τεταρτοκύκλιο στο  , υπολογίστε και τον λόγο :
, υπολογίστε και τον λόγο :  .
.
 έχουν μια γωνία τω βάσεών τους κοινή (
έχουν μια γωνία τω βάσεών τους κοινή (  ) και άρα είναι όμοια .
) και άρα είναι όμοια . .
.  . Από τα όμοια τρίγωνα :
. Από τα όμοια τρίγωνα : 
 σε μέσο κι άκρο λόγο . Αρα
σε μέσο κι άκρο λόγο . Αρα 
 στην
στην  από το Π. Θ. έχω :
από το Π. Θ. έχω : .
.  και έτσι :
και έτσι :  .
.  .
. 