 , για τον οποίον οι γραφικές παραστάσεις των συναρτήσεων :
, για τον οποίον οι γραφικές παραστάσεις των συναρτήσεων :  και :
και :  , έχουν ένα μόνο κοινό σημείο .
, έχουν ένα μόνο κοινό σημείο .Αν χρειαστεί να λύσετε σύστημα , πρέπει να δείξετε ακριβώς πως το λύσατε
Συντονιστής: KAKABASBASILEIOS
 , για τον οποίον οι γραφικές παραστάσεις των συναρτήσεων :
, για τον οποίον οι γραφικές παραστάσεις των συναρτήσεων :  και :
και :  , έχουν ένα μόνο κοινό σημείο .
, έχουν ένα μόνο κοινό σημείο . , για τον οποίον οι γραφικές παραστάσεις των συναρτήσεων :
, για τον οποίον οι γραφικές παραστάσεις των συναρτήσεων :  και :
και :  , έχουν ένα μόνο κοινό σημείο .
, έχουν ένα μόνο κοινό σημείο .θεωρούμε
 έχουμε
έχουμε 
 και τοπικό ελάχιστο για
και τοπικό ελάχιστο για 

Ας δούμε και την απλούστερη , θα ακολουθήσω ακριβώς ότι λέει η εκφώνηση.
 έχω την εξίσωση
έχω την εξίσωση 
 τότε
τότε 
 .
. τότε
τότε 
 .
.Ποιος είναι ο ελάχιστος θετικός αριθμόςγια τον οποίο οι γραφικές παραστάσεις των συναρτήσεων :
και :
, έχουν ένα μόνο κοινό σημείο.
Παρόμοιες με του κ.Χρήστου παραπάνω ήταν και οι δικές μου σκέψεις.
 για το οποία η εξίσωση
για το οποία η εξίσωση  έχει μοναδική λύση. Παρατηρούμε ότι αν για κάποιο
έχει μοναδική λύση. Παρατηρούμε ότι αν για κάποιο  η εξίσωση
η εξίσωση  έχει μια λύση τότε αυτή θα είναι λύση και της εξίσωσης
έχει μια λύση τότε αυτή θα είναι λύση και της εξίσωσης  καθώς και το αντίστροφο. Άρα το πρόβλημα είναι ισοδύναμο με ο να βρούμε
καθώς και το αντίστροφο. Άρα το πρόβλημα είναι ισοδύναμο με ο να βρούμε  για τα οποία η εξίσωση
για τα οποία η εξίσωση  έχει μοναδική λύση.
έχει μοναδική λύση. . Η αλλαγή αυτή δημιουργεί ισοδύναμο πρόβλημα με το αρχικό αφού είναι
. Η αλλαγή αυτή δημιουργεί ισοδύναμο πρόβλημα με το αρχικό αφού είναι  σχέση. Έτσι, ψάχνουμε τα
σχέση. Έτσι, ψάχνουμε τα  για τα οποία η εξίσωση
για τα οποία η εξίσωση  έχει μοναδική λύση.
έχει μοναδική λύση. , ως προς την μονοτονία και τα τοπικά ακρότατα. Η
, ως προς την μονοτονία και τα τοπικά ακρότατα. Η 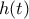 έχει τοπικό μέγιστο
έχει τοπικό μέγιστο  στο σημείο
στο σημείο 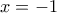 και τοπικό ελάχιστο
και τοπικό ελάχιστο  στο σημείο
στο σημείο 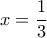 . Από την μονοτονία και τις παραπάνω τιμές των τοπικών ακροτάτων προκύπτει ότι θα υπάρχουν
. Από την μονοτονία και τις παραπάνω τιμές των τοπικών ακροτάτων προκύπτει ότι θα υπάρχουν ![t_{1} \in (-\infty , -1] t_{1} \in (-\infty , -1]](/forum/ext/geomar/texintegr/latexrender/pictures/f2c870608a218975f0a46eac2c5989cd.png) για το οποίο θα ισχύει
για το οποίο θα ισχύει  και
και  για το οποίο
για το οποίο  .
.![[t_{1}, -1] [t_{1}, -1]](/forum/ext/geomar/texintegr/latexrender/pictures/b26c8e917fb2374e4ce8fc63e1ce1faa.png) ,
, ![[-1, \dfrac{1}{3}] [-1, \dfrac{1}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/bb58c79c03e59b1bf4d31742bba3fa7e.png) και
και ![[\dfrac{1}{3}, t_{2}] [\dfrac{1}{3}, t_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/cf1c4ed6442706033c1fa6c0ef5fc791.png) η
η 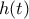 είναι συνεχής. Για κάθε
είναι συνεχής. Για κάθε  που ικανοποιεί την
που ικανοποιεί την  θα υπάρχει ένα τουλάχιστον
θα υπάρχει ένα τουλάχιστον  για το οποίο
για το οποίο  . Δηλαδή στο διάστημα
. Δηλαδή στο διάστημα ![[t_{1}, t_{2}] [t_{1}, t_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/48a9d0f30a334a376a936416c5b74c74.png) υπάρχουν τουλάχιστον τρεις λύσεις. Για
υπάρχουν τουλάχιστον τρεις λύσεις. Για  θα είναι
θα είναι  , άρα δεν θα υπάρχουν τέτοια
, άρα δεν θα υπάρχουν τέτοια  .
.  θα είναι
θα είναι  και λόγο της μονοτονίας για κάθε
και λόγο της μονοτονίας για κάθε  θα υπάρχει μοναδικό
θα υπάρχει μοναδικό  για το οποίο
για το οποίο  .
. .
.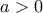 , η συνάρτηση :
, η συνάρτηση :  , είναι κυρτή και δεν παίρνει
, είναι κυρτή και δεν παίρνει  , είναι κοίλη και δεν έχει αρνητικές ρίζες .
, είναι κοίλη και δεν έχει αρνητικές ρίζες . , αν έχουν κοινό σημείο , αυτό θα έχει θετική τετμημένη .
, αν έχουν κοινό σημείο , αυτό θα έχει θετική τετμημένη . ( εδώ θετικό ) για το οποίο να ισχύουν :
( εδώ θετικό ) για το οποίο να ισχύουν : και :
και :  . Αυτά οδηγούν στο σύστημα :
. Αυτά οδηγούν στο σύστημα : 
 . Η μοναδική δεκτή λύση αυτού του συστήματος , είναι η :
. Η μοναδική δεκτή λύση αυτού του συστήματος , είναι η :  .
. , έχουμε δύο σημεία τομής , ενώ για
, έχουμε δύο σημεία τομής , ενώ για  κανένα .
κανένα . , αυτόματα έχουμε κοινό σημείο, με αρνητική
, αυτόματα έχουμε κοινό σημείο, με αρνητική  μικρότερο του
μικρότερο του  , δηλαδή :
, δηλαδή :  .
. , ώστε : "
, ώστε : "γιατί; δηλαδή γιατί πρέπει να "εφάπτονται" στο σημείο;
Christos.N έγραψε: ↑Τρί Δεκ 03, 2019 1:09 pmθεωρούμεέχουμε
Εύκολα βρίσκουμε ότι η συνάρτηση παρουσιάζει δύο τοπικά ακρότατα , τοπικό μέγιστο γιακαι τοπικό ελάχιστο για
Προφανώς...για να έχουμε μοναδική θέση μηδενισμού πρέπει το τοπικό ελάχιστο να είναι θετικό, δηλαδή



Έχουμε δηλαδή το πρόβλημα:
 είναι παραγωγίσιμες στο
είναι παραγωγίσιμες στο  , έτσι ώστε η
, έτσι ώστε η  να είναι γνησίως αύξουσα, και η
να είναι γνησίως αύξουσα, και η  γνησίως φθίνουσα τότε:
γνησίως φθίνουσα τότε: ισχύει ότι η
ισχύει ότι η  είναι γνησίως αύξουσα και δεν μπορεί να έχει δύο άνισες ρίζες.
είναι γνησίως αύξουσα και δεν μπορεί να έχει δύο άνισες ρίζες.  είχαν τρία διαφορετικά κοινά σημεία τότε, από Rolle, η
είχαν τρία διαφορετικά κοινά σημεία τότε, από Rolle, η  θα είχε δύο άνισες ρίζες - άτοπο.
θα είχε δύο άνισες ρίζες - άτοπο. και
και 


Συνεχίζοντας το β.... Αν τώρα υποθέσουμε ότι ηabgd έγραψε: ↑Τετ Δεκ 04, 2019 9:48 pm
Έχουμε δηλαδή το πρόβλημα:
Αν οι συναρτήσειςείναι παραγωγίσιμες στο
, έτσι ώστε η
να είναι γνησίως αύξουσα, και η
γνησίως φθίνουσα τότε:
α. Οι γραφικές τους παραστάσεις μπορούν να έχουν το πολύ δύο κοινά σημεία.
β. Στην περίπτωση που οι γραφικές τους παραστάσεις έχουν ένα ακριβώς κοινό σημείο να εξετάσετε αν "εφάπτονται"
Απάντηση
α. Για τηνισχύει ότι η
είναι γνησίως αύξουσα και δεν μπορεί να έχει δύο άνισες ρίζες.
Αν οι γραφικές παραστάσεις τωνείχαν τρία διαφορετικά κοινά σημεία τότε, από Rolle, η
θα είχε δύο άνισες ρίζες - άτοπο.
β. Όχι. Παράδειγμα: οι συναρτήσειςκαι

 είναι πολυώνυμο και
είναι πολυώνυμο και  η τετμημένη του μοναδικού σημείου τομής των γραφικών παραστάσεων των
η τετμημένη του μοναδικού σημείου τομής των γραφικών παραστάσεων των  τότε:
τότε: 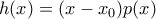 και αν υποθέσουμε ότι
και αν υποθέσουμε ότι  τότε
τότε  και έτσι η
και έτσι η  θα είναι πολυώνυμο περιττού βαθμού. Συνεπώς η
θα είναι πολυώνυμο περιττού βαθμού. Συνεπώς η  θα είναι πολυώνυμο άρτιου βαθμού κάτι που, (μπορεί να δειχθεί εύκολα
θα είναι πολυώνυμο άρτιου βαθμού κάτι που, (μπορεί να δειχθεί εύκολα  είναι γνησίως αύξουσα. Τελικά θα πρέπει
είναι γνησίως αύξουσα. Τελικά θα πρέπει  οπότε
οπότε  και
και  .
.  είναι πολυώνυμο τότε οι γραφικές τους παραστάσεις των
είναι πολυώνυμο τότε οι γραφικές τους παραστάσεις των  "εφάπτονται"
"εφάπτονται"

abgd έγραψε: ↑Τετ Δεκ 04, 2019 11:04 pmΣυνεχίζοντας το β.... Αν τώρα υποθέσουμε ότι ηabgd έγραψε: ↑Τετ Δεκ 04, 2019 9:48 pm
Έχουμε δηλαδή το πρόβλημα:
Αν οι συναρτήσειςείναι παραγωγίσιμες στο
, έτσι ώστε η
να είναι γνησίως αύξουσα, και η
γνησίως φθίνουσα τότε:
α. Οι γραφικές τους παραστάσεις μπορούν να έχουν το πολύ δύο κοινά σημεία.
β. Στην περίπτωση που οι γραφικές τους παραστάσεις έχουν ένα ακριβώς κοινό σημείο να εξετάσετε αν "εφάπτονται"
Απάντηση
α. Για τηνισχύει ότι η
είναι γνησίως αύξουσα και δεν μπορεί να έχει δύο άνισες ρίζες.
Αν οι γραφικές παραστάσεις τωνείχαν τρία διαφορετικά κοινά σημεία τότε, από Rolle, η
θα είχε δύο άνισες ρίζες - άτοπο.
β. Όχι. Παράδειγμα: οι συναρτήσειςκαι

είναι πολυώνυμο και
η τετμημένη του μοναδικού σημείου τομής των γραφικών παραστάσεων των
τότε:
και αν υποθέσουμε ότι
τότε
και έτσι η
θα είναι πολυώνυμο περιττού βαθμού. Συνεπώς η
θα είναι πολυώνυμο άρτιου βαθμού κάτι που, (μπορεί να δειχθεί εύκολα
), είναι αδύνατο αφού η
είναι γνησίως αύξουσα. Τελικά θα πρέπει
οπότε
και
.
Άρα
στην περίπτωση που ηείναι πολυώνυμο τότε οι γραφικές τους παραστάσεις των
"εφάπτονται"

Η
 έχει γνησίως αύξουσα παράγωγο .
έχει γνησίως αύξουσα παράγωγο . έχει γνησίως φθίνουσα παράγωγο.
έχει γνησίως φθίνουσα παράγωγο. έχει μοναδική ρίζα το
έχει μοναδική ρίζα το 
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Δεκ 05, 2019 12:32 pmΗέχει γνησίως αύξουσα παράγωγο .
Ηέχει γνησίως φθίνουσα παράγωγο.
Ηέχει μοναδική ρίζα το

και δεν εφάπτονται εκεί.
Αν δεν μου ξεφεύγει κάτι απαντάω στο ερώτημα σου.
 ,
,  ,
,  και γνησίως φθίνουσα
και γνησίως φθίνουσα  ;
;  είναι γνησίως αύξουσα!! και η
είναι γνησίως αύξουσα!! και η  είναι γνησίως φθίνουσα!!!
είναι γνησίως φθίνουσα!!!

Τίποτα.Απλα την πάτησα.abgd έγραψε: ↑Πέμ Δεκ 05, 2019 5:01 pmΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Δεκ 05, 2019 12:32 pmΗέχει γνησίως αύξουσα παράγωγο .
Ηέχει γνησίως φθίνουσα παράγωγο.
Ηέχει μοναδική ρίζα το

και δεν εφάπτονται εκεί.
Αν δεν μου ξεφεύγει κάτι απαντάω στο ερώτημα σου.
Αν κατάλαβα καλά... εννοείς ότι: οι συναρτήσεις,
οι οποίες έχουν παραγώγους:,
έχουν γνησίως αύξουσακαι γνησίως φθίνουσα
;
Δηλαδή... η συνάρτησηείναι γνησίως αύξουσα!! και η
είναι γνησίως φθίνουσα!!!
...Τι μου κρύβετε;
 παραπάνω . Το λήμμα :
παραπάνω . Το λήμμα :  με την απόλυτη τιμή )
με την απόλυτη τιμή )Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες