 έχει πλευρές :
έχει πλευρές :  . Σημείο
. Σημείο  κινείται επί της
κινείται επί της  .
.Ονομάζω
 τις προβολές του
τις προβολές του  επί των
επί των  αντίστοιχα . Υπολογίστε το :
αντίστοιχα . Υπολογίστε το : 
Παρακαλώ , δημοσιεύστε την λύση σας , μόνον εφόσον έχετε βρει το τελικό αποτέλεσμα
 έχει πλευρές :
έχει πλευρές :  . Σημείο
. Σημείο  κινείται επί της
κινείται επί της  .
. τις προβολές του
τις προβολές του  επί των
επί των  αντίστοιχα . Υπολογίστε το :
αντίστοιχα . Υπολογίστε το : 
Έστω
 και
και  τα ύψη του τριγώνου. Εύκολα με Π. Θ βρίσκω
τα ύψη του τριγώνου. Εύκολα με Π. Θ βρίσκω 
 και στη συνέχεια
και στη συνέχεια 
 και ομοίως
και ομοίως 


 ίσο με
ίσο με 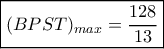
 είναι εγγράψιμο και ο κύκλος του τέμνει ακόμα την
είναι εγγράψιμο και ο κύκλος του τέμνει ακόμα την  στο
στο  .
. .
.  γίνεται μέγιστο όταν το άθροισμα των
γίνεται μέγιστο όταν το άθροισμα των γίνει ελάχιστο .
γίνει ελάχιστο . τα ύψη προς τις υποτείνουσες των πιο πάνω τριγώνων έχω:
τα ύψη προς τις υποτείνουσες των πιο πάνω τριγώνων έχω:  που γίνεται ελάχιστο αν
που γίνεται ελάχιστο αν  .
.
 έχω:
έχω:  Το μέγιστο τότε τετράπλευρο
Το μέγιστο τότε τετράπλευρο 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες