 ορθογώνιο
ορθογώνιο  , θεωρούμε σημεία
, θεωρούμε σημεία 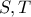 των
των  αντίστοιχα ,
αντίστοιχα ,ώστε :
 . Βρείτε τον λόγο
. Βρείτε τον λόγο  , για τον οποίο μεγιστοποιείται η γωνία
, για τον οποίο μεγιστοποιείται η γωνία  .
. ορθογώνιο
ορθογώνιο  , θεωρούμε σημεία
, θεωρούμε σημεία 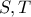 των
των  αντίστοιχα ,
αντίστοιχα , . Βρείτε τον λόγο
. Βρείτε τον λόγο  , για τον οποίο μεγιστοποιείται η γωνία
, για τον οποίο μεγιστοποιείται η γωνία  .
. είναι συνεχής και γνήσια αύξουσα στο
είναι συνεχής και γνήσια αύξουσα στο  .
. μεγιστοποιέιται.
μεγιστοποιέιται. . Εύκολα έχω:
. Εύκολα έχω: 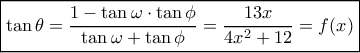 που παρουσιάζει μέγιστο
που παρουσιάζει μέγιστο  και είναι
και είναι 
 σταθερό , το άθροισμά τους γίνεται ελάχιστο όταν
σταθερό , το άθροισμά τους γίνεται ελάχιστο όταν και τότε προφανώς
και τότε προφανώς  γίνεται μέγιστη .
γίνεται μέγιστη . .Από Π.Θ είναι
.Από Π.Θ είναι  και
και 
 και
και 

 η
η  παίρνει ελάχιστη τιμή
παίρνει ελάχιστη τιμή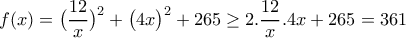 και το ίσον ισχύει όταν
και το ίσον ισχύει όταν 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες