Αν
 ,
,  μη αρνητικοί, τότε
μη αρνητικοί, τότε  .
. ,
,  μη αρνητικοί, τότε
μη αρνητικοί, τότε  .
.Από Cauchy Schwarz,gbaloglou έγραψε: ↑Σάβ Αύγ 10, 2019 9:39 amΠροέκυψε κατά την διάρκεια ανεπιτυχούς προσπάθειας επίλυσης δυσκολώτερου προβλήματος:
Αν,
μη αρνητικοί, τότε
.
 , οπότε
, οπότε  . Οπότε, αρκεί να δείξω ότι
. Οπότε, αρκεί να δείξω ότι ![[abc(a^2+b^2+c^2)]^2 \leqslant 9 [abc(a^2+b^2+c^2)]^2 \leqslant 9](/forum/ext/geomar/texintegr/latexrender/pictures/ee14291aafdc83dc7741415f171f26f8.png) ή αλλιώς
ή αλλιώς  .
. και αρκεί
και αρκεί  .
. , οπότε αρκεί
, οπότε αρκεί  , που είναι προφανής.
, που είναι προφανής.![f(x) = a (b+x) (c-x) \left[ a^2 + (b+x)^2 + (c-x)^2 \right] f(x) = a (b+x) (c-x) \left[ a^2 + (b+x)^2 + (c-x)^2 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/92c4b3372eb068eb591925c6289b3703.png) στο
στο  είναι η
είναι η ![f'(0) = a (b-c) \left[ -a^2 - (b-c)^2 \right] f'(0) = a (b-c) \left[ -a^2 - (b-c)^2 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/5ecb2fe1c0f7350f94b3eb20dd65f80d.png) (ετερόσημη του
(ετερόσημη του  ), από όπου συνάγεται εύκολα ότι η παράσταση μεγιστοποιείται για
), από όπου συνάγεται εύκολα ότι η παράσταση μεγιστοποιείται για  .
.Ορέστη αποδεικνύεις παραπάνω μία κάπως δυσκολότερη ανισότητα από αυτήν που πρότεινα, και που νόμιζα μάλιστα ότι δεν ίσχυε! Δεν χρειάζεται βέβαια Cauchy-Schwartz, αρκεί η ΑΜ-ΓΜ για τηνΟρέστης Λιγνός έγραψε: ↑Σάβ Αύγ 10, 2019 10:01 amΑπό Cauchy Schwarz,gbaloglou έγραψε: ↑Σάβ Αύγ 10, 2019 9:39 amΠροέκυψε κατά την διάρκεια ανεπιτυχούς προσπάθειας επίλυσης δυσκολώτερου προβλήματος:
Αν,
μη αρνητικοί, τότε
.
, οπότε
. Οπότε, αρκεί να δείξω ότι
ή αλλιώς
.
Έστω,και αρκεί
.
Όμως, από την γνωστή, οπότε αρκεί
, που είναι προφανής.
 , οπότε
, οπότε  . (Ο δικός μου τρόπος απόδειξης κοντά στον δικό σου, αλλά περιπετειώδης, καθώς καταλήγει στην
. (Ο δικός μου τρόπος απόδειξης κοντά στον δικό σου, αλλά περιπετειώδης, καθώς καταλήγει στην  , όπου
, όπου  .)
.)
Μία πρώτη προσπάθεια: ηgbaloglou έγραψε: ↑Κυρ Αύγ 11, 2019 10:56 amΟρέστη αποδεικνύεις παραπάνω μία κάπως δυσκολότερη ανισότητα από αυτήν που πρότεινα, και που νόμιζα μάλιστα ότι δεν ίσχυε! Δεν χρειάζεται βέβαια Cauchy-Schwartz, αρκεί η ΑΜ-ΓΜ για τηνΟρέστης Λιγνός έγραψε: ↑Σάβ Αύγ 10, 2019 10:01 amΑπό Cauchy Schwarz,gbaloglou έγραψε: ↑Σάβ Αύγ 10, 2019 9:39 amΠροέκυψε κατά την διάρκεια ανεπιτυχούς προσπάθειας επίλυσης δυσκολώτερου προβλήματος:
Αν,
μη αρνητικοί, τότε
.
, οπότε
. Οπότε, αρκεί να δείξω ότι
ή αλλιώς
.
Έστω,και αρκεί
.
Όμως, από την γνωστή, οπότε αρκεί
, που είναι προφανής.
, οπότε
. (Ο δικός μου τρόπος απόδειξης κοντά στον δικό σου, αλλά περιπετειώδης, καθώς καταλήγει στην
, όπου
.)
Αλλά μια και μιλάμε για Cauchy-Schwartz ... παρατηρώ ότι με χρήση της ανάγεται η κυκλική, μη συμμετρική ανισότητα που πρότεινες αρχικά (εδώ) στην εξής συμμετρική ανισότητα:
Η παραπάνω ανισότητα ισχύει, αλλά δεν βλέπω κάποιον αποδεκτό τρόπο απόδειξης. Όποιος δει κάτι ας μας διαφωτίσει, είτε εδώ είτε εκεί!
 οδηγεί σε ισότητες όπως οι
οδηγεί σε ισότητες όπως οι 



 ,
,  πάντοτε, στην
πάντοτε, στην
Αρχικά έστωgbaloglou έγραψε: ↑Κυρ Αύγ 11, 2019 10:56 amΑλλά μια και μιλάμε για Cauchy-Schwartz ... παρατηρώ ότι με χρήση της ανάγεται η κυκλική, μη συμμετρική ανισότητα που πρότεινες αρχικά (εδώ) στην εξής συμμετρική ανισότητα:
Η παραπάνω ανισότητα ισχύει, αλλά δεν βλέπω κάποιον αποδεκτό τρόπο απόδειξης. Όποιος δει κάτι ας μας διαφωτίσει, είτε εδώ είτε εκεί!
 κλπ.
κλπ.
 ) η δοσμένη γράφεται:
) η δοσμένη γράφεται:
 είναι φανερό ότι επιτυγχάνεται όταν δύο μεταβλητές (εκ των
είναι φανερό ότι επιτυγχάνεται όταν δύο μεταβλητές (εκ των  ) είναι ίσες, αφού είναι δευτεροβάθμια.
) είναι ίσες, αφού είναι δευτεροβάθμια. 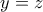 . Αλλάζουμε ξανά τις μεταβλητές και καταλήγουμε ότι πρέπει να ισχύει:
. Αλλάζουμε ξανά τις μεταβλητές και καταλήγουμε ότι πρέπει να ισχύει: αν
αν  που όμως δεν ισχύει πχ. για
που όμως δεν ισχύει πχ. για  .
.
Χάρη σ' ευχαριστώ πολύ για την επισήμανση: πράγματι η ανισότητα που πρότεινα δεν ισχύει, έστω και οριακά -- τόσο οριακά (μέγιστη τιμή αριστερού σκέλους μικρότερη τουΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε: ↑Τρί Αύγ 13, 2019 9:45 pmΑρχικά έστωgbaloglou έγραψε: ↑Κυρ Αύγ 11, 2019 10:56 amΑλλά μια και μιλάμε για Cauchy-Schwartz ... παρατηρώ ότι με χρήση της ανάγεται η κυκλική, μη συμμετρική ανισότητα που πρότεινες αρχικά (εδώ) στην εξής συμμετρική ανισότητα:
Η παραπάνω ανισότητα ισχύει, αλλά δεν βλέπω κάποιον αποδεκτό τρόπο απόδειξης. Όποιος δει κάτι ας μας διαφωτίσει, είτε εδώ είτε εκεί!κλπ.
Αν χρησιμοποιήσουμε την αντικατάσταση
(δηλ.) η δοσμένη γράφεται:
Όμως η μέγιστη τιμή τηςείναι φανερό ότι επιτυγχάνεται όταν δύο μεταβλητές (εκ των
) είναι ίσες, αφού είναι δευτεροβάθμια.
Συνεπώς υποθέτουμε. Αλλάζουμε ξανά τις μεταβλητές και καταλήγουμε ότι πρέπει να ισχύει:
αν
που όμως δεν ισχύει πχ. για
.
Ως εκ τούτου προκύπτει το αντιπαράδειγμα στην αρχική ανισότητα
ΥΓ. Να επαναφέρω ακόμα μια φορά την: https://www.mathematica.gr/forum/viewto ... 80&t=64959
 ) ... που οδήγησε σε λάθος και το ίδιο το WolframAlpha (βλέπε συνημμένο)!
) ... που οδήγησε σε λάθος και το ίδιο το WolframAlpha (βλέπε συνημμένο)!Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες